Основы криптографии: от математики до физики
Авторизуйтесь
Основы криптографии: от математики до физики
Основы криптографии включают шифры, специальную терминологию и отдельные компоненты криптосистемы. Сегодня эта наука тесно связана с информационной безопасностью.
Примечание Вы читаете улучшенную версию некогда выпущенной нами статьи.
Задачи, которые решает криптография:
- Конфиденциальность — когда нужно передать данные так, чтобы человек, перехвативший зашифрованное сообщение, не смог узнать его содержание.
- Аутентификация — получатель сообщения хочет быть уверен, что оно пришло от определённой стороны, а не от кого-либо ещё.
- Целостность — получатель сообщения хочет доказательства того, что оно не было изменено третьей стороной.
- Отказ от ответственности — предотвратить отказ автора за создание или отправку сообщения.
Популярные шифры
Чтобы понять основы шифрования, необходимо обратиться к популярным примерам.
Квадрат Полибия
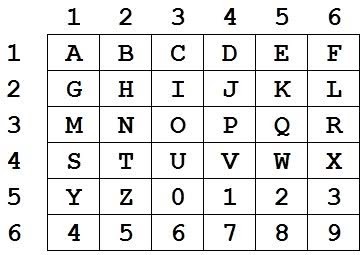
Квадрат Полибия — шифр простой замены. В данном примере будет использоваться двумерная матрица 6х6, содержащая заглавные буквы алфавита и цифры от 0 до 9:
С матрицей 6х6 (36 буквенно-цифровых знаков) мы можем начать замену. Например, буква «А» имеет адрес 1х1 или x=1, y=1. Эту запись можно упростить до 11. Другой пример: адрес буквы «N» будет 2х3 или x=2, y=3 или 23.
- Сообщение: ENCRYPT ME 2 DAY
- Шифротекст: 51–23–31–63–15–43–24 13–51 55 41–11–15
Шифр может сделать достаточно длинным и сложным, используя прописные буквы и специальные символы. Также повторение символов и написание алфавита вразброс может дать непредсказуемый результат, устойчивый для метода полного перебора.
Шифр Цезаря
Шифр Цезаря считается самым первым. Цезарь использовал его для кодирования сообщений своим генералам, чтобы враги из Римской Империи не смогли прочитать приказы при перехвате. Шифр Цезаря имеет элементарную форму шифрования, и сегодня его легко взломать: алфавит просто сдвигается вправо или влево. Разные значения сдвига приводят к разным результатам шифровки. Число сдвига — это число букв, на которое происходит смещение в одну из сторон, для создания шифротекста.
Пример использования шифра со сдвигом влево на 3:
- Сообщение: ENCRYPT ME
- Шифротекст: HQFUBSW PH
Шифротекст выше может быть легко взломан методом полного перебора, который заключается в сдвиге в одну из сторон на одну позицию, пока не получится какое-то смысловое сообщение.
Прим. пер. Существует более простой способ взлома шифра Цезаря — частотный анализ. Он заключается в подсчёте частоты встреч каждого символа в любом обычном тексте и в шифротексте. Потом символы с похожими частотами заменяются. Например, если в шифротексте чаще всего встречается буква «T», то она заменяется на букву «Е» для английского алфавита. Этот способ действует только для текстов свыше 300 символов.
Квадрат Виженера
Это усовершенствованный шифр Цезаря с разными значениями сдвига. Например, к первой букве сообщения применяется преобразование ROT5, ко второй — ROT16, etc.
Также у нас есть статья, из которой вы узнаете о самых популярных кодах и шифрах.
Полиморфизм
Основы шифрования и криптографии включают в себя полиморфизм. Это более продвинутая практика в криптографии и часто используется в техниках компьютерного шифрования. Такая техника, которая самостоятельно модифицирует криптоалгоритм после каждого выполнения, и на каждой итерации получаются разные результаты. Если понадобится зашифровать одну и ту же информацию два раза, то алгоритм выдаст разные шифротексты.
Распространённые алгоритмы
Сегодня шифры используют алгоритмы либо с секретным, либо с публичным ключом. В шифрах с закрытым ключом используется единственный ключ, которым обмениваются стороны. Такой ключ или шифр также называют симметричным.
В 1949 году Клод Шеннон из Bell Laboratories опубликовал фундаментальную теорию, положившую начало симметричному шифрованию, а десятилетия эволюции принесли примеры высокого качества. Однако только в 1975 году мощный алгоритм с закрытым ключом DES стал доступен для общего пользования.
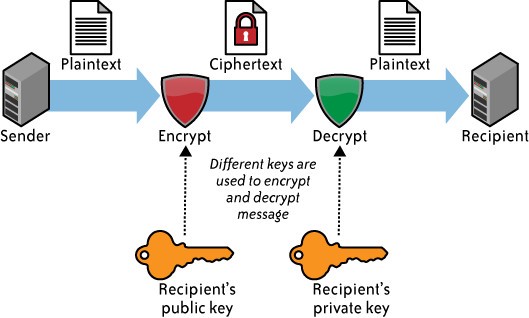
Шифрование с помощью открытого ключа или асимметричное шифрование также возникло в середине 1970-х. Асимметричные шифры используют пару ключей — открытый, им делятся с другими людьми, и соответствующий ему закрытый, пользователь должен хранить его в секрете от других.
Стойкость шифровального алгоритма зависит от трёх важных факторов:
- Инфраструктура — если криптография встроена в ПО, то самым слабым звеном будет среда выполнения этого ПО.
- Длина ключа — практичный шифр должен использовать такую длину ключа, при которой полный перебор будет нецелесообразным.
- Качество алгоритма — ошибки шифрования могут ускорить процесс взлома для злоумышленников.
Виды алгоритмов
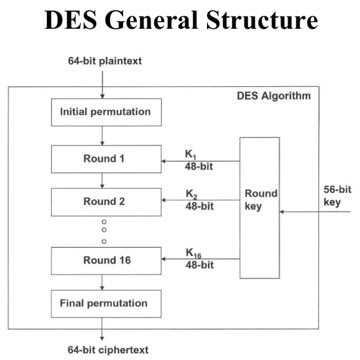
DES выдержал испытание временем и вошёл в основы криптографии. После четверти века исследований учёным удалось найти несколько спекулятивных атак, которые в конечном итоге не были столь эффективными, как метод полного перебора. Единственная реальная слабость DES-шифра — маленькая длина ключа в 56 бит.
Triple DES (3DES) — модификация DES, позволяющая увеличить длину ключа до 112 или 168 бит.
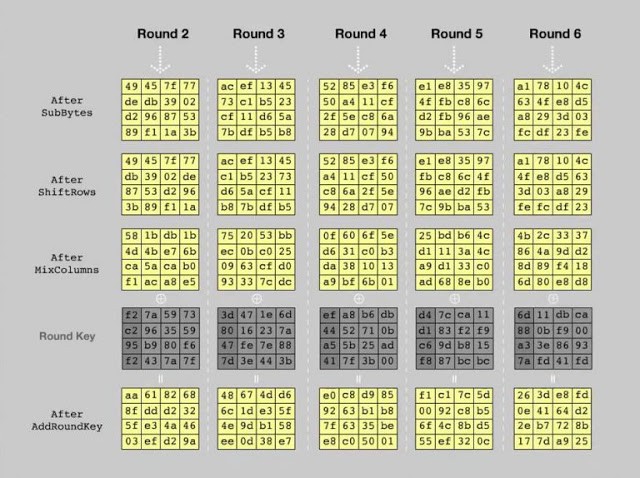
AES (Advanced Encryption Standard или Rijndael) поддерживает три длины ключа: 128, 192 и 256 бит. Использует 128-битный размер блоков. Считается стойким и используется по всему миру.
Алгоритм шифрования Rijndael (AES)
Так как DES был специально разработан для аппаратного обеспечения, то не было предусмотрено, чтобы он эффективно работал в ПО. NIST протестировал работу алгоритма AES в программной среде и разработал требования к хранению криптоматериала, чтобы гарантировать, что AES будет эффективно работать на C и Java, которые используются на рабочих станциях, а также в более ограниченных средах встроенных процессоров ARM и смарт-карт.
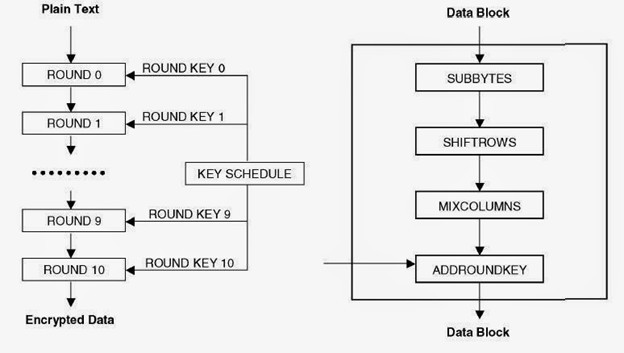
Архитектура AES основана на принципе, известном как замена и перестановка, и быстро работает как в программном, так и на аппаратном уровнях. В отличие от своего предшественника — DES, AES не использует сеть Фейстеля.
Длина ключа, используемого для шифрования AES, указывает на количество повторений раундов преобразования, которые преобразуют входной сигнал, называемый исходным текстом, а конечный вывод — шифротекстом. Число циклов повторения выглядит следующим образом:
- 10 циклов повторения для 128-битных ключей;
- 12 циклов повторения для 192-битных ключей;
- 14 циклов повторения для 256-битных ключей.
Каждый раунд состоит из нескольких этапов обработки. Набор обратных повторений применяется для преобразования шифротекста в исходный текст с использованием того же самого ключа шифрования.
Квантовая криптография
Это уже не совсем основы криптографии, а более продвинутый уровень.
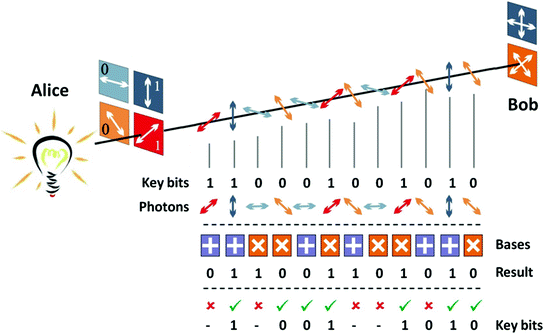
На приведённой диаграмме квантовое распределение ключей (протокол BB84), являющееся безопасным способом связи, который реализует криптографический протокол с участием компонентов квантовой механики. Он позволяет двум сторонам создавать общий закрытый ключ, известный только им.
Новое поколение криптографии будет основываться не на математике, а на физике. Учёные в области физики атомов и частиц уже вошли в мир основ криптографии и хотят использовать законы квантовой механики для отправки сообщений, которые невозможно взломать. Они основоположники новой науки — квантовой криптографии.
Источник
Шифрование и математика
Разделы: Математика
Основная цель – на популярном, практически игровом уровне познакомить учащихся с применением математики для решения задач кодирования и декодирования информации.
I. Постановка задачи.
II. Секретная переписка подпольщиков.
III. Роль математики в расшифровке. Способ шифровки — кодирование, декодирование.
IV. Матричный способ шифровки.
I. Зачем нужно шифровать те или иные тексты, от содержащих государственные тайны — до записок знакомой девочке или мальчику?
Веками создавались самые различные системы тайнописи, которыми владели только «посвященные», умевшие и зашифровать текст, и расшифровать его. Конечно, для «непосвященных» разгадать шифр всегда было очень важно. Поэтому веками разрабатывались как способы расшифровки чужих шифров, так и способы создания своих шифров, которые не поддавались бы расшифровке. Проблема расшифровки связана не только с секретами, которые следует скрыть от посторонних, но и с серьезными проблемами гуманитарных наук – например, истории и археологии, прежде всего с «воскрешением» так называемых мертвых языков. Так, древняя цивилизация в Египте оставалась за семью печатями до тех пор, пока в XIX веке французский филолог Шампольон не смог расшифровать иероглифы, которые древним египтянам были хорошо понятны. А в XX в. Наш соотечественник, ученый, историк, лингвист и этнограф Ю.В.Кнозоров расшифровал письменность древнего народа майя, жившего много веков назад на территории нынешней Мексики.
II. Послушайте рассказ о секретной переписке подпольщиков. [2]
Революционер – подпольщик вынужден вести свои записи и переписку с товарищами таким образом, чтобы никто из посторонних не мог понять написанного. Для этого пользуются особым способом письма, называемым «тайнописью». Придуманы разные системы тайнописи; к их услугам прибегают не одни подпольщики, но также дипломаты и военные для сохранения государственных тайн. Сегодня я хочу рассказать об одном из таких способов ведения секретной переписки, а именно: о так называемом способе «решетки». Он принадлежит к числу сравнительно простых и тесно связан с арифметикой.
Желающие вести тайную переписку по этому способу запасаются каждый «решеткой», т.е. бумажным квадратиком с прорезанными окошечками. . (Раздается ученикам «решетки»).
Пусть требуется послать товарищу такую записку:
Собрание делегатов отмените.
Полиция кем-то предупреждена. Антон.
Наложив решетку на листок бумаги, подпольщик пишет сообщение букву за буквой в окошечках решетки. Так как окошек 16, то сначала помещается только часть записки:
Сняв решетку, вы увидите запись, представленную на рисунке 2,
Здесь, разумеется, ничего засекреченного пока нет: каждый легко поймет, в чем дело. Но это только начало; записка в таком виде не останется. Подпольщик поворачивает решетку «по часовой стрелке» на четверть оборота, т.е. располагает ее на том же листке так, что цифра 2, бывшая раньше сбоку, теперь оказывается вверху. При новом положении решетки все раньше написанные буквы заслонены, а в окошечках появляется чистая бумага. В них пишут следующие 16 букв секретного сообщения.
Такую запись не поймет не только посторонний человек, но и сам писавший, если позабудет текст своего сообщения.
Чтобы писать дальше, надо вновь повернуть решетку на четверть оборота по часовой стрелке. Она закроет все написанное и откроет новые 16 свободных клеток.
Наконец делается последний поворот решетки цифрой «4» вверх, и в открывшиеся 16 чистых квадратиков вписывают окончание записки. Так как остаются три неиспользованные клетки, их заполняют буквами а, б, в – просто для того, чтобы в записке не оказалось пробелов.
Письмо имеет вид, представленный на рисунке 3.
Попробуйте в нем что-нибудь разобрать! Пусть записка попадет в руки полиции, пусть полицейские сколько угодно подозревают, что в ней скрыто важное сообщение, — догадаться о содержании записки они не смогут. Никто из посторонних не разберет в ней ни единого слова. Прочесть ее в состоянии только адресат, имеющий в руках точно такую же решетку, как и та, которой пользовался отправитель.
Как же прочтет адресат это секретное письмо? Он наложит свою решетку на текст, обратив ее цифрой «1 вверх, и выпишет те буквы, которые появятся в окошечках. Это будут первые 16 букв сообщения. Затем повернет решетку — и перед ним предстанут следующие 16 букв. После четвертого поворота вся секретная записка будет прочитана.
III. Огромную роль в проблеме расшифровки текстов играет, как ни странным это может показаться, математика, прежде всего теория вероятностей и математическая статистика. [1]
Сегодня мы с вами познакомимся с одним очень простым способом шифрования. Чтобы воспользоваться им для шифровки и расшифровки ( кодирования и декодирования), достаточно знать лишь простейшую арифметику, порядок букв в алфавите и помнить всего… четыре числа. А расшифровать ваш текст непосвященному человеку будет абсолютно не под силу.
Для кодирования текста на русском языке занумеруем все буквы по месту их расположения в алфавите – от 1 до 33, добавив 34-ю пробел.
Возьмем какое-нибудь простое предложение, например, «шёл снег», и каждую букву заменим соответствующей цифрой. Получим последовательность: 26,7, 13, 34, 19, 15, 6, 4.
IV. Построим из этой последовательности две таблички 2х2:
Такие таблички из четырех чисел называются матрицей.
Зашифруем эту последовательность с помощью еще одной матрицы 
Такой способ шифрования и называют матричным. Ваш адресат получит текст: 91, 116, 52, 75, 56, 42, 31, 23.
А как же он его расшифрует? Оказывается, и это нетрудно: он должен взять декодирующую матрицу
и проделать с полученным текстом то же самое, что делали мы с исходным текстом.
После замены матриц на последовательность 26,7, 13, 34, 19, 15, 6, 4, а затем — чисел на буквы дешифровальщик получит исходный текст «шёл снег».
Ясно, что никто посторонний, не знающий ни кодирующей, ни декодирующей матрицы, получить этот текст не сможет.
Однако матричный способ шифрования не смог бы существовать, если бы в качестве кодирующей можно было брать только матрицу
На самом деле таких матриц бесконечно много, придумывать их очень легко. И вообще вы можете менять свою систему «тайнописи» каждый день. Для этого нужно знать очень немного – уметь любые две матрицы «перемножать», т.е. по определенному правилу составлять из них третью.

А теперь, по правилу умножения:
1. Перемножьте матрицы:
2. Зашифруйте текст «Вы мне дороги».
На следующем занятии мы поговорим с вами об алгебре матриц, а также будем друг-другу писать письма, а для этого необходимо будет придумать свою кодирующую матрицу. Подумайте о том, какая у вас будет эта матрица?
1. Дорофеев Г.В. и др. Курс по выбору для 9 класса «Избранные вопросы математики»//Математика в школе, 2003, № 10, с. 2-36.
2. Я.И.Перельман «Живая математика».- М.: Издательство «Просвещение», 1995.
Источник