Способы с помощью которых выполняются действия

Действие включает в качестве необходимого компонента акт создания в виде постановки и удержания цели. Но действие есть одновременно и акт поведения, так как человек совершает внешние движения в процессе деятельности. Однако в отличие от бихевиоризма, эти движения рассматриваются А.Н.Леонтьевым в неразрывном единстве с сознанием. Таким образом, действие есть единство противоположных сторон:

Надо отметить, что действия диктуются логикой социальной и предметной среды, то есть в своих действиях человек должен учитывать свойства предметов, на которые он воздействует. Например, когда вы включаете телевизор или пользуетесь компьютером, вы соотносите свои действия с устройством этих приборов. Действие может рассматриваться с позиции, что должно быть постигнуто и как это должно быть достигнуто, то есть каким способом. Способ выполнения действия называется операцией. Представим это схематически:

Любое действие осуществляется определенными операциями. Представьте, что вам нужно совершить действие—перемножить два двузначных числа, например 22 и 13. Как вы это будете делать? Кто-то перемножит их в уме, кто-то будет письменно (в столбик), а если под рукой есть калькулятор, то вы воспользуетесь им. Таким образом, это будут три разных операции одного и того же действия. Операции характеризуют техническую сторону выполнения действия, и когда говорят о ловкости, сноровке («золотые руки»), то это относится именно к уровню операций.

От чего же зависит характер используемых операций, то есть почему в упомянутом выше случае действие умножения можно совершить тремя разными операциями? Операция зависит от условии, в которых она совершается. Под условиями подразумеваются как внешние обстоятельства (в нашем примере — наличие или отсутствие калькулятора), так и возможности, внутренние средства самого действующего субъекта (кто-то прекрасно считает в уме, а для кого-то необходимо осуществить это на бумаге).

Главное свойство операций состоит в том, что они мало или совсем не осознаются. Этим операции принципиально отличаются от действий, которые предполагают сознательный контроль за их выполнением. Например, когда вы записываете лекцию, то совершаете действие: вы стараетесь понять смысл высказываний преподавателя и зафиксировать это на бумаге. В процессе этого действия вы выполняете операции. Так, написание любого слова состоит из определенных операций: например, чтобы написать букву «а» нужно выполнить овал и крючок. Разумеется, что вы об этом не задумываетесь, вы это делаете автоматически. Отмечу, что граница между действием и операцией очень подвижное действие может переходить в операцию, операция в действие. Например, для первоклассника написание буквы «а» есть действие, так как перед ним стоит цель овладеть способом написания этой буквы. Однако постепенно он все меньше и меньше задумывается над тем, из каких элементов она состоит и как их писать, и действие превращается в операцию. Представим дальше, что вы решили сделать красивую надпись на открытке — очевидно, что все ваше внимание будет направлено, прежде всего, на сам процесс написания. В этом случае операция становится действием.

Источник

Способы с помощью которых выполняются действия

Любая деятельность может быть представлена как взаимодействие двигательных актов, регулирования, контроля.

Определение. Приемы деятельности — способы исполнения контроля и регулирования.

К основным приемам деятельности относят навыки, привычки, умения.

1. Навыки. Важнейшим приемом деятельности является навык.

Определение. Навык — автоматизированное действие, сформированное путем многократного повторения, характеризующееся высокой степенью освоения и отсутствием поэлементной сознательной регуляции и контроля.

Навыки образуются на основе упражнений, многократных повторений действий. В результате происходит количественное и качественное преобразование действий. Произвольные действия превращаются в непроизвольные, автоматизированные.

Различают несколько видов навыков : перцептивные, интеллектуальные и двигательные.

Перцептивный навык — это автоматизированное чувственное отражение свойств и характеристик хорошо знакомого, неоднократно воспринимавшегося ранее предмета.

Интеллектуальный навык — автоматизированный прием, способ решения встречавшейся ранее задачи, достижения цели.

Двигательный навык — автоматизированное воздействие на внешний объект с помощью движения с целью его преобразования, неоднократно осуществлявшееся ранее.

Формирование навыков может осуществляться двумя методами:

1) методом «проб и ошибок»;

2) через систему сознательных процедур.

Метод «проб и ошибок» малоэффективен, поскольку он требует длительного времени на освоение навыка и не гарантирует его надежного закрепления. Высокоэффективной считается выработка навыка через систему сознательных процедур.

Метод сознательных процедур основывается на понимании. В выработке навыка по этой методике осуществляются четыре этапа :

1) предварительное ознакомление , осмысливание действий, которые выполняются некачественно;

2) подготовительный этап , на котором действие совершается сознательно, но неумело;

3) стандартизирующий этап , на котором происходит частичная автоматизация действий;

4) варьирующий (ситуативный) этап, который характеризуется свободным выполнением действия в разных условиях в автоматическом режиме.

2. Привычка. Близкой навыку по механизмам формирования и характеру осуществления является привычка.

Определение. Привычка — это автоматизированное действие, выполнение которого стало потребностью личности.

Привычка, как и навык, формируется путем многократного повторения, но отличается от него. Навык — это возможность выполнения действия, которое в себе не содержит стимуляции к данному действию. Привычка же предполагает побуждение производить данное действие.

3. Умение. Навык и привычка тесно связаны с умением.

Определение. Умение — это освоенный субъектом способ выполнения действия, обеспечиваемый совокупностью приобретенных знаний и навыков.

Умение — основа мастерства. В отличие от привычки, оно создает возможность выполнения действия не только в привычных условиях, но и в изменившейся ситуации.

Источник

Какими бывают способы выполнения:

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: научать — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «способ&raquo

Ассоциации к слову «выполнение&raquo

Синонимы к слову «способ&raquo

Синонимы к слову «выполнение&raquo

Предложения со словосочетанием «способы выполнения&raquo

Они постоянно ищут новые и лучшие способы выполнения стоящих перед ними задач.

Цитаты из русской классики со словосочетанием «способы выполнения»

Весь день я раздумывал, каким образом я выполню принятые обязательства, или, лучше сказать, каким способом уклонюсь от их выполнения .

Значение слова «способ&raquo

СПО́СОБ , -а, м. Образ действий, прием осуществления чего-л. Способ изготовления стекла. Решение задачи различными способами. (Малый академический словарь, МАС)

Значение слова «выполнение&raquo

ВЫПОЛНЕ́НИЕ , -я, ср. Действие по знач. глаг. выполнить—выполнять. Выполнение задания. Выполнение плана. Выполнение работы. (Малый академический словарь, МАС)

Афоризмы русских писателей со словом «способ&raquo

Стихи — совершеннейший из способов пользоваться человеческим словом, и разменивать его на мелочи, пользоваться им для пустяков — грешно и стыдно…

Отправить комментарий

Дополнительно

Значение слова «способ&raquo

СПО́СОБ , -а, м. Образ действий, прием осуществления чего-л. Способ изготовления стекла. Решение задачи различными способами.

Значение слова «выполнение&raquo

ВЫПОЛНЕ́НИЕ , -я, ср. Действие по знач. глаг. выполнить—выполнять. Выполнение задания. Выполнение плана. Выполнение работы.

Предложения со словосочетанием «способы выполнения&raquo

Они постоянно ищут новые и лучшие способы выполнения стоящих перед ними задач.

Вид и способ выполнения выбираются в соответствии с проектной схемой.

Мышление возникает тогда, когда неизвестны способы выполнения задачи.

Синонимы к слову «способ&raquo

Синонимы к слову «выполнение&raquo

Ассоциации к слову «способ&raquo

Ассоциации к слову «выполнение&raquo

Сочетаемость слова «способ&raquo

Сочетаемость слова «выполнение&raquo

Морфология

Правописание

Карта слов и выражений русского языка

Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.

Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.

Сайт оснащён мощной системой поиска с поддержкой русской морфологии.

Источник

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

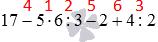
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Источник