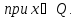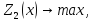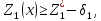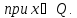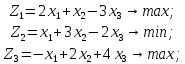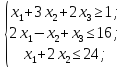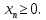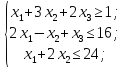Способы решения задачи многокритериальной оптимизации

Решение задач многокритериальной оптимизации

Ранее в разделе примеров мы рассматривали задачи с единственной целевой функцией. Но если качество решения (выбор стратегии) оценивается по нескольким критериям сразу? Тогда получаем нетривиальную задачу: выбор наилучшего решения для нескольких целевых функций одновременно.

Обычно используют понятие эффективного (оптимального по Парето) решения (точнее, нескольких решени, иногда их даже бесконечно много, что ставит еще одну задачу выбора).

Решение задачи векторной оптимизации обычно сводят к решению одной или последовательности однокритериальных задач. Основные методы: свертка критериев, оптимизация главного локального критерия, метод последовательных уступок.

Ниже вы найдете подробные примеры решений по этой теме — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий, перейдите в раздел: Контрольные работы по линейному программированию.

Многокритериальная оптимизация: примеры решений

Задача 1. Сформулировать экономическую задачу с двумя критериями эффективности и не менее 4 условий (ограничений).
Двумя способами:
1) методом идеальной точки
2) сведением к ЗЛП
Решая задачу вторым методом, добавьте дополнительное условие (ограничение) от ЛПР — обоснуйте. Сделать выводы по полученным данным.

Задача 2. Определить тип задачи и найти оптимальное решение, всеми способами. Фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы A1 A2, А3 А4). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в таблице.

Задача 3. Полуфабрикаты поступают на предприятие в виде листов фанеры. Всего имеется две партии материала, причем первая партия содержит 400 листов, а вторая 250 листов фанеры. Из поступающих листов фанеры необходимо изготовить комплекты двух видов. Комплект первого вида включает 4 детали 1-го типа, 3 детали 2-го типа и 2 детали 3-го типа. Комплект второго вида включает 2 детали 1-го типа, 4 детали 2-го типа и 3 детали 3-го типа. Лист фанеры каждой партии может раскраиваться различными способами. Количество деталей каждого типа, которое получается при раскрое одного листа соответствующей партии по тому или иному способу раскроя, представлено в следующей таблице. Стоимость одного листа первой партии составляет 1000 руб., а стоимость одного листа второй партии – 1200 руб. Цена комплекта первого вида составляет 150 руб., цена комплекта второго вида – 200 руб.
Необходимо решить многокритериальную задачу.
Критерий 1. Максимизация прибыли от продажи всех комплектов деталей.
Критерий 2. Максимизация количества комплектов первого вида.
Критерий 3. Максимизация количества комплектов второго вида.
Примечание: для построения Парето-оптимального множества рассмотреть только критерии 2,3..

Задача 4. Дана задача векторной оптимизации: $$ z_1=-5x_1+2x_2 \to \max,\\ z_2=-3x_1+x_2 \to \max,\\ z_3=3x_1 \to \max,\\ x_1+x_2 \le 18,\\ 1 \le x_1 \le 10,\\ 1 \le x_2 \le 9. $$ Требуется определить переговорное множество, а затем решить данную задачу методом последовательных уступок (допустимые уступки по первым двум критериям принять равными $\delta_1=3$ и $\delta_2=2$).

Задача 5. Возможные значения курса базовой валюты в течении ближайшего года представлены четырьмя интервалами. Банк рассматривает четыре инвестиционных проекта, каждый из которых связан с международным бизнесом. Последствия от принятия банком го инвестиционного проекта при условии, что курс валюты окажется в м интервале, приведены в таблице 1. В таблице 2 приведены прогнозируемые экспертами вероятности возможных интервалов курса базовой валюты.
Требуется построить матрицу сожалений, найти решения, рекомендуемые правила Вальда, Сэвиджа, максимального ожидаемого дохода и минимального ожидаемого риска, а также определить проекты, оптимальные по Паретто. .

Источник

5.2. Методы решения многокритериальной задачи оптимизации

Метод обобщенного критерия . Метод перехода от несколь-

ких критериев f 1 , f 2 ,… f m к одному, задаваемому новой функцией

называется сверткой или методом обобщенного крите-

α j называются весовыми коэффициентами. Чем больше

α j , тем больший «вклад» вносит j -й критерий в обобщенный крите-

рий z . Иногда требуют, чтобы ∑ α j = 1 .

Пример 5.3. Решить задачу методом обобщенного критерия

Решение. Пусть α 1

= 0,6 . Тогда задача двухкритери-

альной оптимизации сводится

к задаче одного критерия

z = α 1 f 1 + α 2 f 2 = 0,4(4x 1 + x 2 ) + 0,6(x 1 + 2 x 2 ) = 2,2x 1 + 1,6x 2 → max

x 1 + x 2 + x 3 = 7 x 1 + x 4 = 5 x 2 + x 5 = 4

Перепишем целевую функцию z в виде z − 2,2x 1 − 1,6 x 2 = 0 . Составим начальную симплекс-таблицу

Вводим в базис переменную x 1 и, так как

дим из базиса x 4 .

Вводим в базис переменную x 2

дим из базиса x 3 .

Последняя строка и столбец свободных членов содержит только положительные числа, следовательно, мы получили опти-

f 2 * = f 2 (5;2) = 9 .

5.2. Выбор весовых

Метод приоритетов. Метод приоритетов решения много-

критериальных задач применяется в том случае, когда критерии f i

упорядочены по их относительной важности.

На первом шаге решения задачи отбирают множество исходов, которые имеют максимальную оценку по важнейшему критерию. Если исход единственный, то он и является оптимальным. Если же исходов несколько, то среди них выбирают те, которые имеют максимальную оценку по второму по важности критерию. Если опять исходов несколько, то процесс повторяют для следующих критерий.

Пример 5.4. Решить двухкритериальную задачу методом приоритетов.

Источник

Раздел 2. Методы решения задачи многокритериальной оптимизации

Чтобы получить более полную характеристику достоинств и недостатков проектируемого объекта, нужно ввести больше критериев качества в рассмотрение. Как результат, задачи проектирования сложных систем всегда многокритериальные, так как при выборе наилучшего варианта приходится учитывать много различных требований, предъявленных к системе [28].

С привычной точки зрения задача со многими критериями решения не имеет, но к счастью это не так, всегда есть возможность одновременного удовлетворения всех заданных условий [51]. А так, как практически любая подобная ситуация допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны.

Перечислим некоторые из подходов к решению задач многокритериальной оптимизации:

1. Метод уступок – лицо, принимающее решения подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.

2. Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему варианту.

3. Метод свертывая – лицо, принимающее решения сводит многокритериальную задачу к задаче с одним критерием.

Ниже, рассмотрим подробно этих методов решения задачи многокритериальной оптимизации [33,46,48,51].

2.1. Метод последовательных уступок

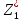
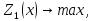
Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности [51]. Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Вначале определяется максимальное значение , первого по важности критерия в области допустимых решений, решив задачу

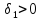
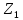
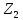
Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения (экономически оправданной уступки) критерияи отыскивается максимальное значение второго критерияпри условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, т.е. решается задача

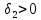
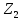
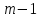
Снова назначается величина уступки по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия и т.д. Наконец, выявляется экстремальное значение последнего по важности критерияпри условии, что значение каждого из первыхчастных критериев отличается от экстремального не более чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным.

Существенным недостатком метода последовательных уступок является то, что решение, полученное этим методом, может оказаться неоптимальным по Парето [37].

Рассмотрим пример, математическая модель трехкритериальной задачи имеет вид [51]:

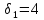
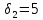
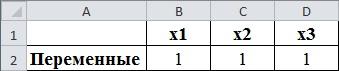
Уступка по первому критерию , а по второму.

Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные 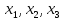. Для этого в ячейку А2 вводим подпись «Переменные», а соседние три ячейки В2, С2 и D2 вводим значения переменных. Это могут быть произвольные числа, например единицы или нули, далее они будут оптимизироваться.

рис. 2.1. Определение переменных значений

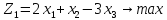
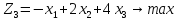
В третьей строке задаем целевые функции. В А3 вводим подпись «Целевые», а в В3 формулой «=2*B2+C2-3*D2» задаем первую целевую функцию . Аналогично в С3 и D3 вводим вторуюи третьюцелевую функцию, вводя в С3 «=B2+3*C2-2*D2», а в D3 «=-B2+2*C2+4*D2».

рис.2.2. Определение целевых значений

Ячейка А5 будем называть «Ограничения».

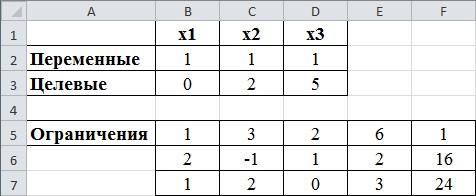
Левые части ограничений распишем от B5:D7, правые части записываем в диапазонF5:F7. Вводим в Е5 формулу «=B5*$B$2+C5*$C$2+D5*$D$2», номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки Е6 и Е7.

рис.2.3. Определение ограничений

Предварительные действия завершены. Вызываем надстройку «Поиск решения» в меню «Данные».

На первом этапе оптимизируем первую целевую функцию. После открытия окна «Поиск решения» в поле «Оптимизировать целевую функцию» ставим курсор и делаем ссылку на ячейку «В3», щелкая по ней мышью. В окне появится $B$3. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Максимум».

После ставим курсор в поле «Изменяя ячейки переменных» и обводим ячейки с переменными В2, С2 и D2, выделяя ячейки с переменными. В поле появиться $B$2:$D$2.

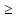
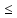
В нижней части окна находится поле «Ограничения». Для того, чтобы ввести ограничения, нажимаем кнопку «Добавить», откроется окно «Добавление ограничения». В левом поле «Ссылка на ячейки» вводят ссылку на левую часть первого ограничения – ячейку «Е5», в центральном окне определяем знак«»и в правом «Ограничения» выбираем соответствующую правую часть первого ограничения –«F5». Нажимаем «ОК», видим, что ограничение появилось в окне. Нажимаем вновь «Добавить», вводим «E6» «» и «F6». Вновь нажимаем «Добавить», вводим «E7» «≤» и «F7».

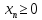
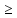
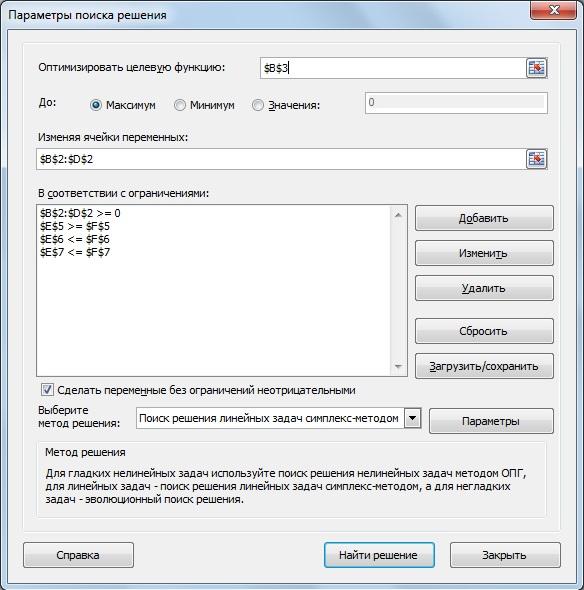
Для ввода дополнительных ограничений вновь нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В2, С2 и D2 (результат $B$2:$D$2) в среднем окне ставим «» и в правом число 0.

рис. 2.4. Параметры поиска решения

Далее выбираем метод решения «Поиск решения линейных задач симплекс-методом». Для запуска вычислений нажимаем кнопку «Найти решение». Появляется надпись, что решение найдено.

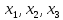
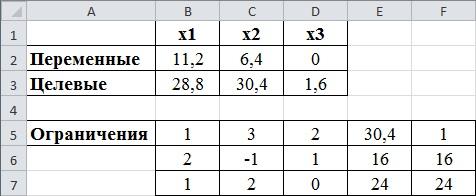
Выбираем «Сохранить найденное решение» и «ОК» видим результат. В ячейках В2, С2 и D2 видны значения переменных соответствующие оптимальному решению: 11,2; 6,4 и 0. В ячейки В3 – значение целевой функции 28,8.

рис.2.5. Результат полученного решения

На втором этапе оптимизируется вторая целевая функция. Однако, первую, в соответствие с методом последовательных уступок, можно ухудшить первый критерий на величину не более, чем 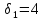. По этой причине, на втором шаге, значения в ячейке В3 (где хранится первая целевая функция, которая максимизируется) может быть значение, не меньшее, чем 24,8 (=28,8-4). Для удобства, можно записать «Уступок» в сторонке.

Вызываем надстройку «Поиск решения», видно, что все прежние данные остались введенными. Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке С3, в которой находится ссылка на вторую целевую функцию. Так, как вторая целевая минимизируется, то ставим флажок в поле напротив надписи «Минимум». Вводим дополнительное ограничение, связанное с уступкой по первому критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить», правее поля. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В3», «≥», «С9».

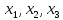
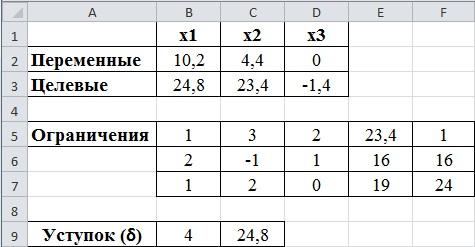
Результат – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С3). Первая равна своему минимальному значению 24,8 (ячейка В3).

рис.2.6. Определение уступка

На третьем этапе делаем уступку по второму критерию. Величина уступки равна 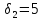. Так, как вторая функция минимизируется, то ее значение не должно превышать 23,4+5=28,4. Вызываем надстройку «Поиск решения». Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке D3, в которой находится ссылка на третью целевую функцию. Так, как третья целевая максимизируется, то ставим флажок в поле напротив надписи «Максимум». Вводим дополнительное ограничение, связанное с уступкой по второму критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить». В появившемся окне «Добавление ограничения», вводим данные «С3», «≤», «С10».

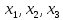
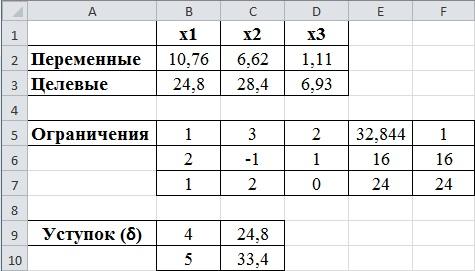
Результат – переменные равны 10,76; 6,62; 1,11. Целевые функции равны, соответственно, 24,8; 28,4 и 6,93. Это окончательный ответ. Все дополнительные условия соблюдены.

рис.2.7. Окончательный результат решения по методу последовательного уступка

Источник