Нестандартные способы решения задач на ОГЭ

Содержит материал по применению формулы Пика и метода Пирсона при решении зкзаменационных задач по математике
Просмотр содержимого документа
«Нестандартные способы решения задач на ОГЭ»
Нестандартные способы решения задач на ОГЭ
Князева Ольга Юрьевна
Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.
На доске записано число. Заранее приготовлена презентация к уроку, способствующая интересному и наглядному проведению урока.
Проверьте свою готовность к уроку. На столе должны лежать тетрадь, дневник, пенал.
Провести параллели с темой последних.
Какую тему изучаем? Задачи какого типа решали на прошлом уроке? Какие формулы для решения задач нам понадобились?
Вычисление площадей фигур на клетчатой бумаге
Постановка целей и задач.
Продолжите фразу: «Сегодня на уроке мы будем вычислять…» (Сегодня на уроке мы будем вычислять площади различных фигур на клетчатой бумаге.)
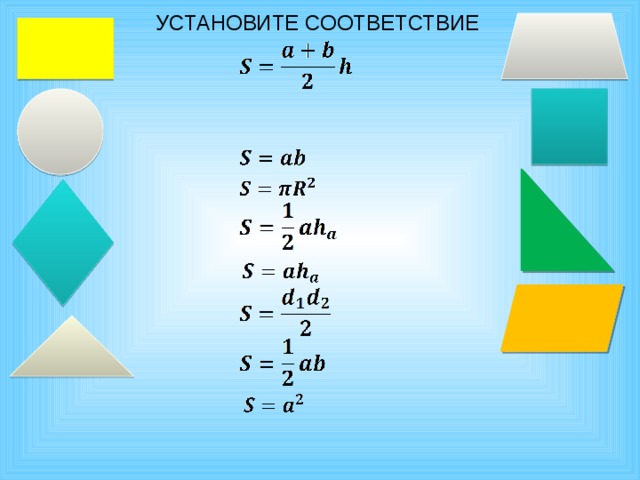
« Не бойтесь формул! Учитесь владеть этим инструментом человеческого гения! В формулах заключено величие и могущество разума…» Марков А. А.
Давайте повторим основные формулы нахождения площадей, которые нам пригодятся сегодня на уроке.
Необходимо нажать на формулу маркером от интерактивной доски для проверки.
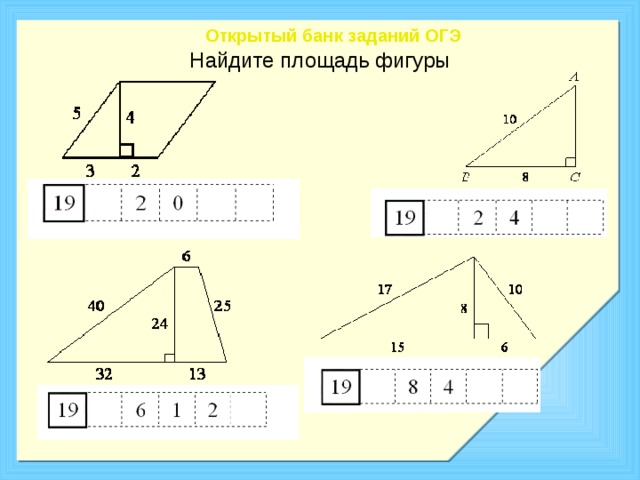
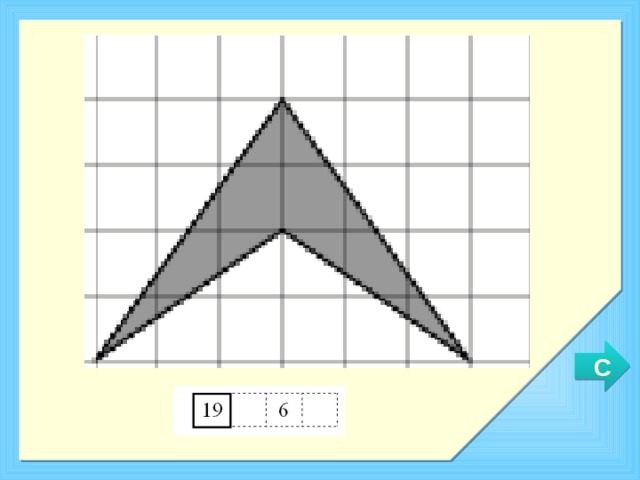
Открытый банк заданий ОГЭ
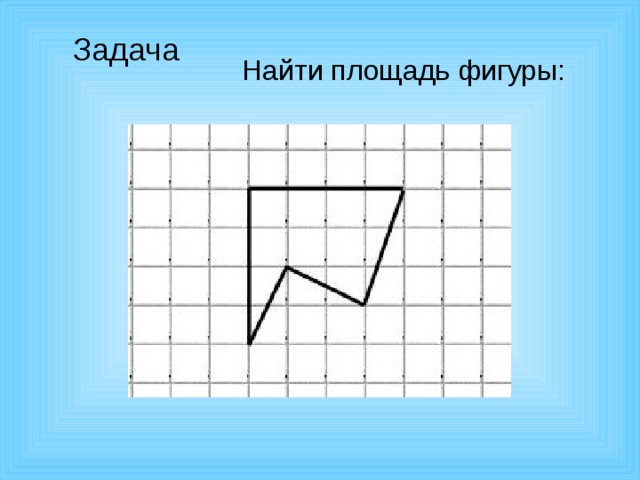
Найдите площадь фигуры
А теперь применим наши знания на практике. Перед вами задачи, которые были взяты из открытого банка заданий ОГЭ на сайте ФИПИ.
Ваша задача предложить самый простой способ нахождения площади, вычислить и предложить план нахождения альтернативного способа.
Вычисления вы можете делать в рабочей тетрадях.
Обратите внимание на форму записи в бланках ответов.
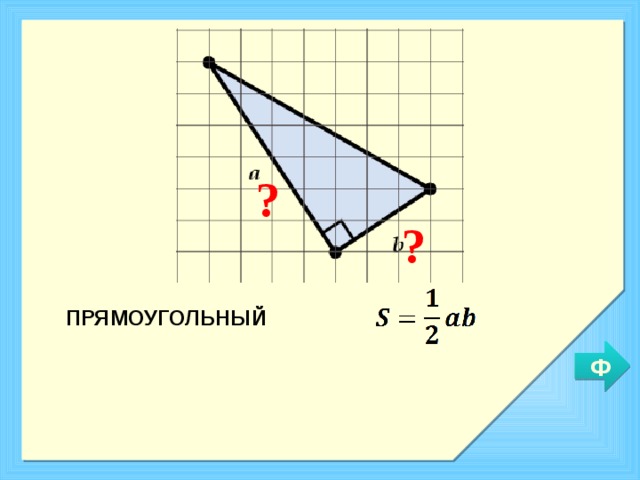
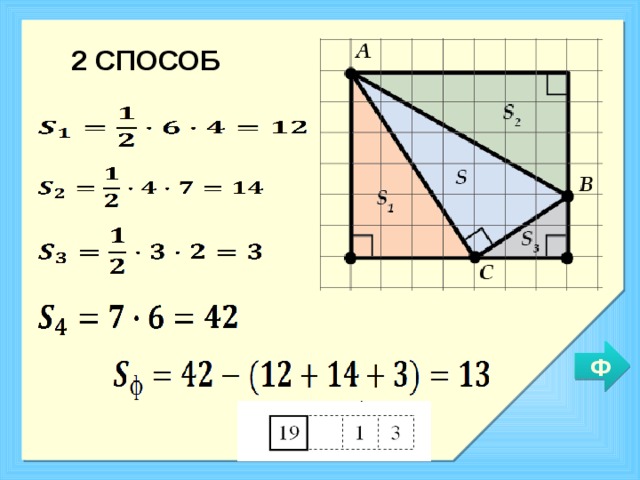
Есть несколько способов, разберемся с первым:
Попытаемся найти a и b.
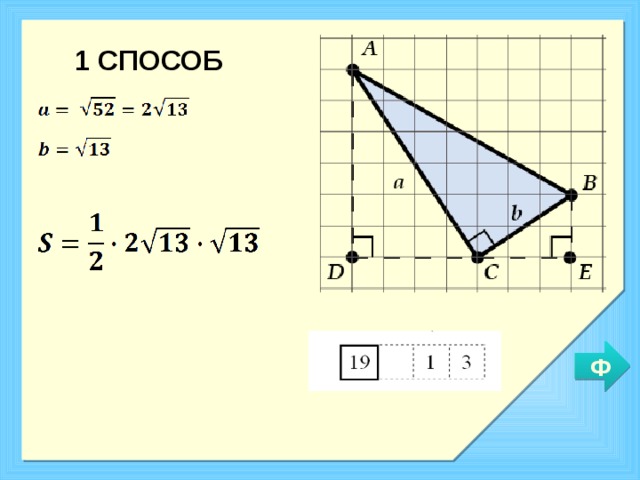
Построим дополнительные прямоугольные треугольники. На листе в клетку легко посчитать длину их катетов.
Найдем a по теореме Пифагора из ΔADC, а b по теореме Пифагора из ΔBCE.
Попробуем дополнить наш треугольник до “хорошего” многоугольника, то есть до такого, площадь которого мы сможем вычислить, потом из полученного числа вычесть площади добавленных частей.
Нужно окружить нашу фигуру прямоугольником.
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку! Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника.
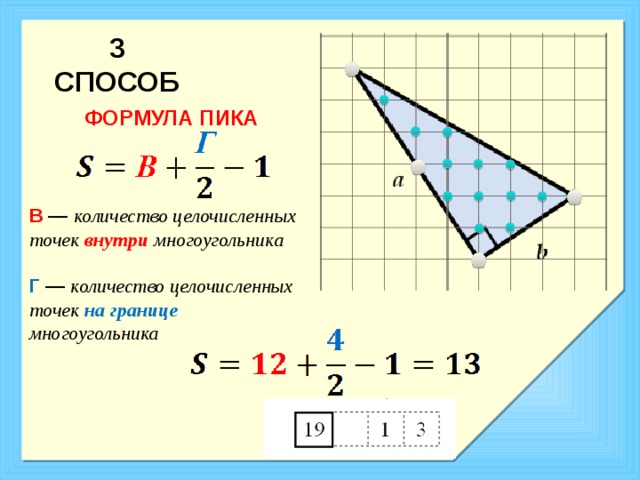
Георг Александр Пик,
Формула была открыта в 1899 г.
Площадь искомой фигуры можно найти по формуле:
- Г – количество узлов на границе треугольника (на сторонах и вершинах):
- В – количество узлов внутри треугольника;
* Под «узлами» имеется ввиду пересечение линий.
В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе многоугольника
Знакомы ли вам элементы данного чертежа?
Точка координатной плоскости называется целочисленной, если обе её координаты целые числа.
Площадь многоугольника с целочисленными вершинами равна S=В+Г\2-1
Данная формула позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.
Формула Пика очень удобна когда сложно догадаться, как разбить фигуру на удобные многоугольники или достроить.
Герг Алекса́ндр Пик— австрийский математик. Жил в Праге и преподавал в Немецком университете.
Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер в возрасте 82 лет.
Найти площадь фигуры:
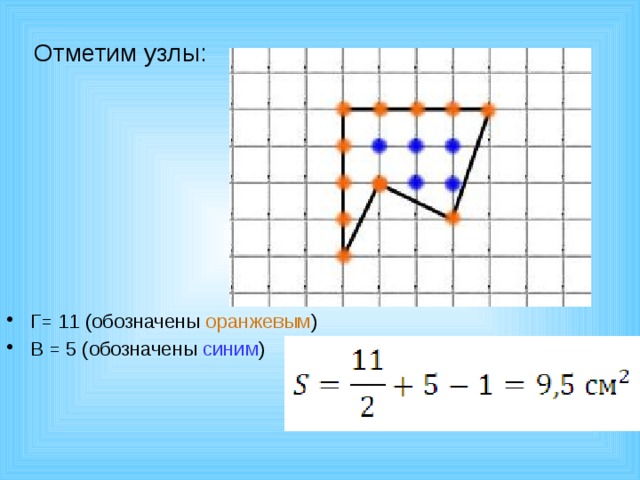
- Г= 11 (обозначены оранжевым )
- В = 5 (обозначены синим )
Решение задания 2 различными способами. Выполнение необходимых чертежей на слайде с помощью интерактивной доски.
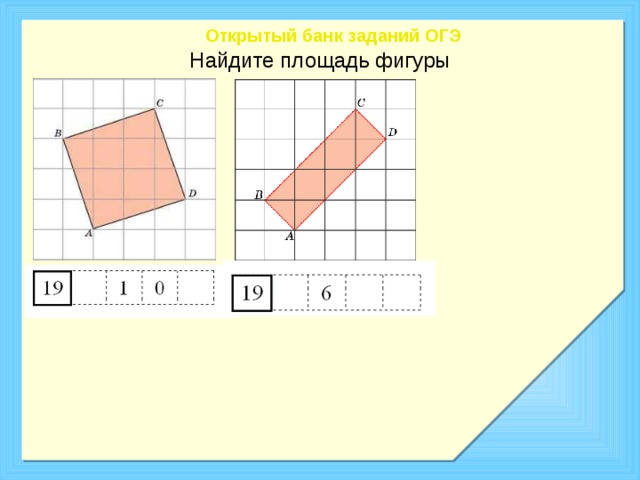
Открытый банк заданий ОГЭ
Найдите площадь фигуры
На следующем слайде задание прежнее. Но есть и отличия. В чем они заключаются? Можем ли мы применить прямое использование формулы? Почему? Сталкивались ли вы с подобными заданиями и где?
Где мы применяли знания используя клетки?
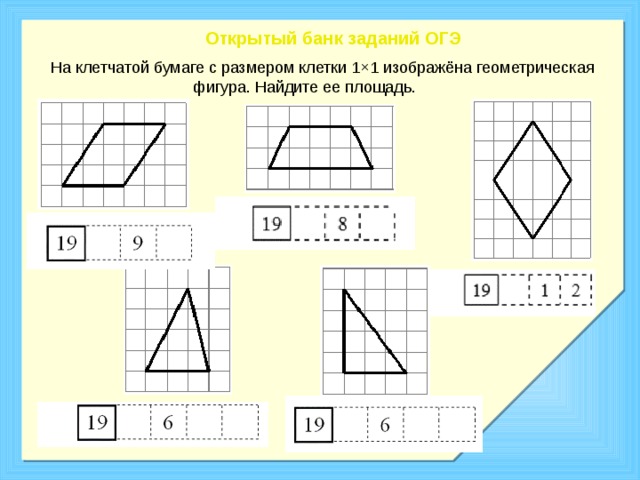
Открытый банк заданий ОГЭ
На клетчатой бумаге с размером клетки 1×1 изображёна геометрическая фигура. Найдите ее площадь.
Устно решим задания из открытого банка заданий ОГЭ на сайте ФИПИ. Вычисления вы можете делать в рабочей тетрадях.
Решение задания тремя различными способами.
Какой способ проверить верно ли вы нашли площадь? Ответы во всех способах должны быть одинаковые.
Выполнение необходимых чертежей на слайде с помощью интерактивной доски.
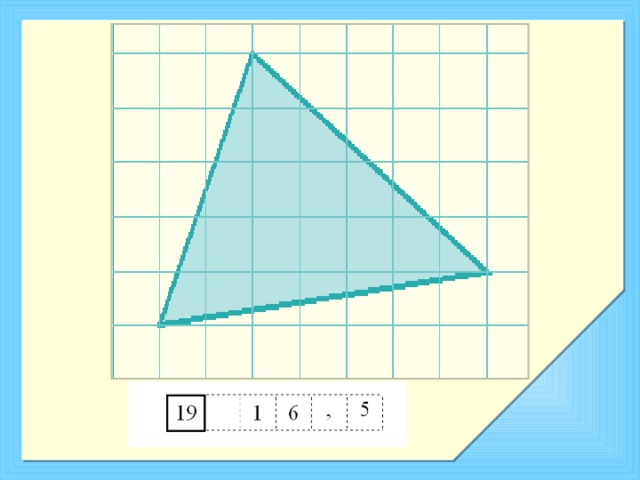
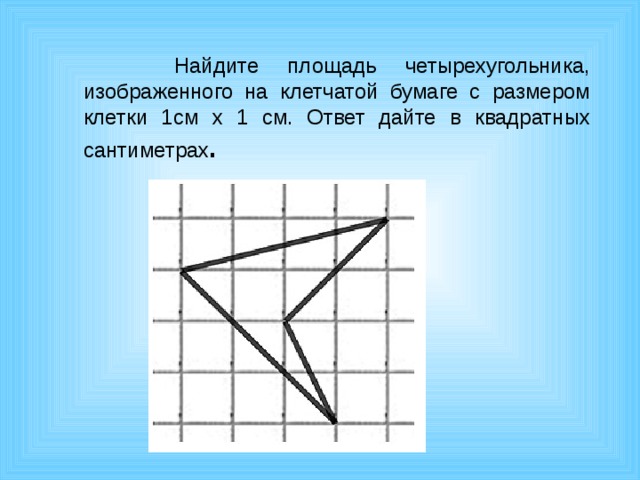
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1 см. Ответ дайте в квадратных сантиметрах .
- Решение задач на смеси и сплавы
Задачи на «концентрацию», на «смеси и сплавы»
— концентрация(доля чистого вещества в смеси)
-количество чистого вещества в смеси
масса смеси х концентрация = количество чистого вещества.
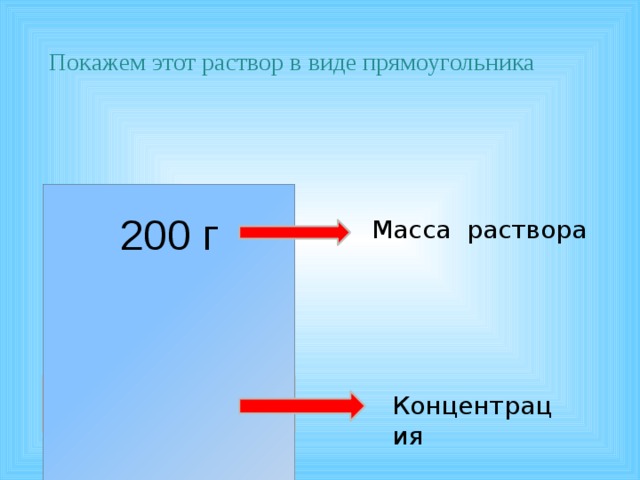
Возьмем 180 грамм воды и добавим в воду 20 грамм соли. Получим раствор соли , его масса равна 180 + 20 = 200 грамм.
соли) — это отношение количества
соли к количеству раствора,
записанное в процентах —
(20 : 200) ·100 = 10%
Покажем этот раствор в виде прямоугольника
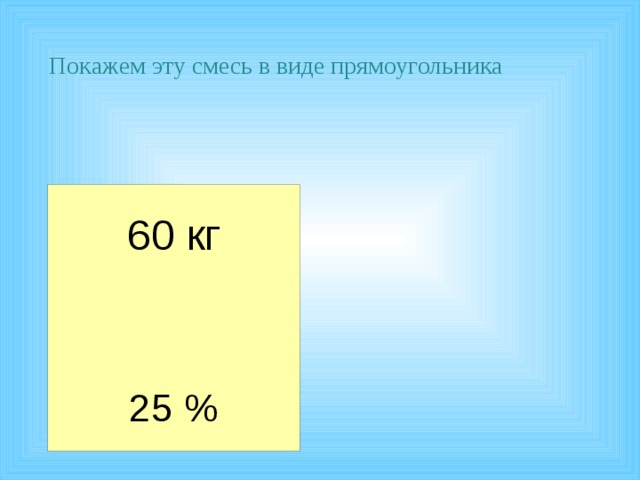
Возьмем 15 кг цемента и 45 кг песка, высыпим содержимое ведер в ящик и тщательно перемешаем цемент с песком. Получим смесь цемента с песком, её масса равна 15 кг + 45 кг = 60 кг.
цемента к количеству
Покажем эту смесь в виде прямоугольника
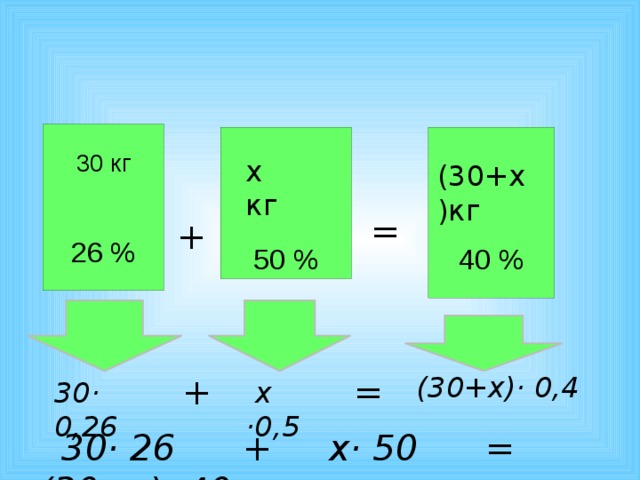
Имеется 30 кг 26% го раствора соли. Требуется получить 40% раствор соли. Сколько кг 50% раствора соли нужно добавить?
30· 26 + х· 50 = (30+х)· 40
В бидоне было 3 литра молока 6% жирности. После того как в бидон добавили некоторое количество молока 2% жирности и тщательно
перемешали, получили молоко с жирностью 3,2%. Сколько литров молока 2% жирности было добавлено в бидон?
Выберите правильный рисунок к этой задаче.
Выберите правильное уравнение.
Из чаши, содержащей 300 граммов 6% раствора уксусной кислоты, отлили некоторое количество этого раствора и добавили такое же количество воды. Определите, сколько граммов воды было добавлено, если известно, что в результате получили 2%-ый раствор уксусной кислоты
Нарисуйте и заполните рисунок
300 · 6 – 6х + х·0 = 300 · 2
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Составим систему уравнений:
Решая ее, получаем х=60, у=30.
при решении задач на смеси и сплавы
решения задач «на смеси, сплавы»
Примем некоторые допущения:
- Все получающиеся сплавы или смеси однородны.
- При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
- Определение.Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.
- процентное содержание вещества;
- концентрация вещества;
- массовая доля вещества. Всё это синонимы.
Готовим раствор определенной концентрации. Имеется 2 раствора с более высокой и менее высокой концентрацией, чем нужно.
Обозначим массу 1-го раствора m 1 , а 2-го m 2 , тогда при смешивании масса смеси будет равна сумме этих масс. Массовая доля растворённого вещества в 1-м растворе – q 1 , во 2-м – q 2 , а в их смеси – q 3 . Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах: m 1 q 1 + m 2 q 2 =q 3 (m 1 + m 2 ), m 1 (q 1 – q 3 ) = m 2 (q 3 – q 2 )
Отношение массы 1-го раствора к массе 2-го раствора это отношение разности массовых долей растворённого вещ-ва в смеси и в 2-м растворе к разности величин в 1-м растворе и в смеси.
При решении задач на растворы с разными концентрациями чаще всего применяют квадрат Пирсона.
При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
Задача 4. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?
Задача 5 . Из сосуда, доверху наполненного 97% раствором кислоты, отлили 2 литра жидкости и долили 2 литра 45% раствора этой же кислоты. После этого в сосуде получился 81% раствор кислоты. Сколько литров раствора вмещает сосуд?
Смешали 500 г 10%-го раствора соли и 400 г 55%-го раствора соли. Определите концентрацию соли в смеси.
Ответ : концентрация соли в смеси двух исходных растворов 30%.
Задача 7. Имеются два слитка, содержащие медь. Масса второго слитка на 3 кг больше, чем масса первого слитка. Процентное содержание меди в первом слитке – 10%, во втором – 40%. После сплавления этих двух слитков, получился слиток, процентное содержание меди в котором 30%. Определить массу полученного слитка.
Задача 8. Сплавили 300 г сплава олова и меди, содержащего 60% олова, и 900г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве?
Задача 9. В сосуд, содержащий 5 литров 12-процентного водного
раствора некоторого вещества, добавили 7 литров воды. Сколько
процентов составляет концентрация получившегося раствора?
1) Смешали 3 литра 25-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
2) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
3) Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава.
4) Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси?
- В 5 кг сплава олова и цинка содержится 80% цинка. Сколько кг олова надо добавить к этому сплаву, чтобы процентное содержание цинка стало 40%?
- Имеется 4 литра 20%-го раствора спирта. Сколько воды него нужно, чтобы получился 10%-й раствор спирта?
- Имелось два сплава серебра. Процент содержания серебра в первом сплаве был на 25% выше, чем во втором. Когда их сплавили вместе, то получили сплав, содержащий 30% серебра. Найдите вес сплавов, если в первом сплаве было 4кг, а во- втором 8 кг.
- Имеется два раствора некоторого вещества. Один 15%-ный, а второй 65%-ный Сколько нужно взять литров каждого раствора, чтобы получить 200л раствора, содержание вещества в котором равно 30%?
- В какой пропорции нужно смешать 10-ный и 15-ный растворы аммиачной селитры, чтобы приготовить из них 15-ный раствор селитры.
- Если к сплаву меди и цинка добавить 20г меди, то содержание меди в сплаве станет равным 70%. Если же к первоначальному сплав добавить 70г сплава, содержащего 40% меди, то содержание меди станет равным 52%. Найдите первоначальный вес сплава.
Математика-наука интересная, сложная,
поэтому нельзя упускать ни одной возможности
сделать её более доступной!
Спасибо за внимание
Если вы хотите научиться плавать,
то смело входите в воду, а если хотите научиться решать задачи,
Источник