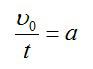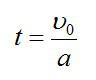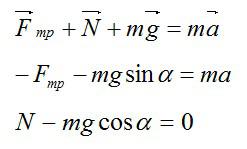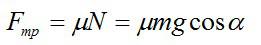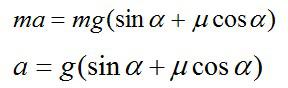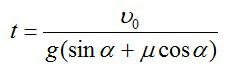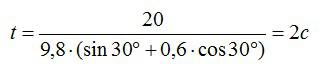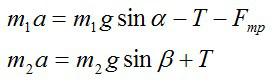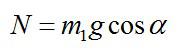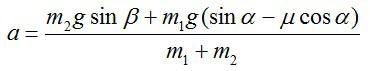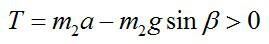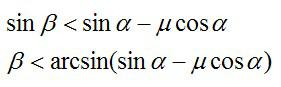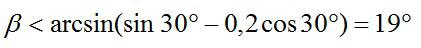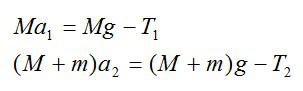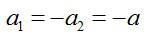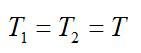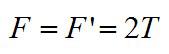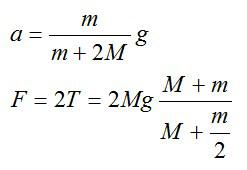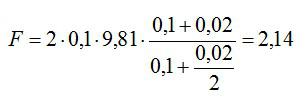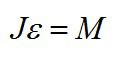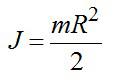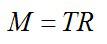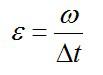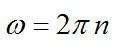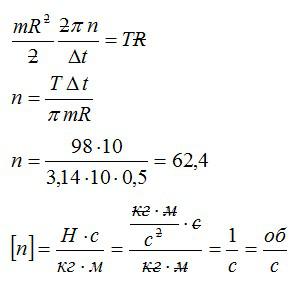Способы решения задач динамики

Алгоритм решения задач по динамике

Обновлено: 30 Июня 2021

Физика — серьезная наука, которая состоит из нескольких крупных разделов и множества менее объемных подразделов. Проще всего с каждым из них знакомиться отдельно, чтобы избежать путаницы в голове. В этой статье подробно поговорим о динамике.

Что такое динамика в физике

Динамика в физике — это раздел механики, который изучает взаимодействие тел и причины возникновения/изменения движения.

Динамика, которая опирается на законы Ньютона, называется классической. Этот раздел изучает движение объектов со скоростями в пределах от миллиметров в секунду до километров в секунду. В классической механике причинами движения всегда выступают силы. Законы динамики изучают также:

• движение упруго и пластически деформируемых тел;
• жидкостей;
• газов.

Не все виды движения можно описать законами динамики. Например, движение элементарных частиц при скоростях, близких к скорости света, подчиняется другим физическим законам.

В ходе изучения динамики конкретных объектов, возникли специальные дисциплины:

• баллистика;
• небесная механика;
• динамика корабля и самолёта и др.

Основные понятия и определение

Классическая механика изучает такие понятия, как:

• масса;
• энергия;
• импульс;
• момент импульса;
• сила;
• равнодействующая сила и др.

Масса — это скалярная физическая величина, которая является характеристикой такого свойства объекта, как инертность, и определяет количество вещества в теле.

Энергия — это количественная мера, характеризующая движение и взаимодействие объектов, а также их способность воздействовать на окружающий мир.

Импульс — это векторная физическая величина, измеряющая механическое движение тела, которая рассчитывается по формуле: \vec p=m\times\vec v

Момент импульса — это количественная характеристика вращательного движения.

Сила — это векторная величина, которая является причиной изменения скорости тела или его деформации, а также количественной мерой взаимодействия тел.

Любая сила в физике характеризуется 3 параметрами:

• точкой приложения;
• направлением;
• численным значением или модулем.

Линией действия силы называют прямую, вдоль которой эта сила действует.

Равнодействующая сила — это сила, которая оказывает на тело такое же действие, как все другие вместе взятые силы, воздействующие на него. Величина рассчитывается по формуле:

\(\vec F=\vec F_1+\vec F_2+\vec F_3 \)

В том случае, когда объект находится в состоянии покоя, равнодействующая всех сил, действующих на него, равна нулю.

В динамике встречаются следующие виды сил:

1. Тяжести. Приложена к центру массы тела и направлена вертикально вниз (всегда перпендикулярно горизонту). Рассчитывается по формуле: \(F=m\times g\) где \(m\) — масса тела, \(g\) — ускорение свободного падения.
2. Трения. Приложена к поверхности касания тела и опоры и направлена в противоположную сторону той, куда направлены другие силы, действующие на тело. Вычисляется по формуле: \(F=\mu\times N\) , где \(\mu\) — коэффициент трения, \(N\) — сила реакции опоры.
3. Сопротивления. Возникает при движении тела в газе или жидкости, всегда направлена против скорости движения.
4. Реакции опоры. Действует на тело со стороны опоры, направлена перпендикулярно от нее.
5. Натяжения нити. Направлена от тела вдоль нити.
6. Упругости. Возникает при деформации тела, направлена против деформации. Вычисляется она согласно закону Гука по формуле: \(F=k\times\Delta l\) , где \(k\) — коэффициент упругости, \(\Delta l\) — удлинение тела при деформации.

Основные законы динамики, формулы

Законы, на которых строится динамика, были впервые сформулированы Исааком Ньютоном в 1687 году. Именно поэтому их чаще всего и называют законами Ньютона.

Законы Ньютона верны только для описания движений, которые происходят в инерциальных системах отсчета (ИСО). Инерциальной называют такую систему отсчета, в которой тела двигаются равномерно и прямолинейно.

Первый закон Ньютона

Согласно первому закона Ньютона, тело остается в покое или равномерно прямолинейно движется, если на него не действуют никакие силы или равнодействующая всех сил равна нулю.

Инерцией называется способность тел сохранять скорость движения при отсутствии воздействия на него других объектов. Иногда первый закон Ньютона называют еще законом инерции.

Второй закон Ньютона

Второй закон Ньютона считается основным законом динамики и представляет собой формулу нахождения ускорения: ускорение, которое приобретает тело, прямо пропорционально равнодействующей сил (F), воздействующих на тело и обратно пропорционально массе ( \(m\) ) этого тела:

Когд на тело действуют сразу несколько сил, под силой в этом уравнении подразумевается равнодействующая всех сил.

Третий закон Ньютона

Третий закон Ньютона гласит: тела воздействуют друг на друга с силами, которые равны по модулю и противоположны по направлению, лежат на одной прямой и имеют одну физическую природу:

Данные силы не могут уравновесить друг друга, так как приложены к разным телам. По этой же причине их нельзя складывать.

Методы решения задач, алгоритм

Как правило, все задачи из раздела динамики решаются с использованием законов Исаака Ньютона.

Для того, чтобы существенно упростить процесс решения задач по динамике, нужно:

1. Внимательно прочитать условие задачи, разобраться, какие силы воздействуют на тела, указанные в задании.
2. Нарисовать рисунок, на котором изобразить все векторные силы и указать их направление.
3. Выбрать систему отсчета: одну координатную ось направить по направлению ускорения рассматриваемого тела, другую — перпендикулярно ускорению.
4. Вспомнить второй закон Ньютона: \(\vec F_1+\vec F_2+\vec F_3=m\times \vec a\)
5. Записать скалярную форму уравнения, учитывая, что силы, которые направлены против выбранных осей координат, будут иметь отрицательные значения. Получится такая система уравнений: \(\left\<\beginF_<1x>+F_<2x>+F_<3x>=m\times a_x\\F_<1y>+F_<2y>+F_<3y>=m\times a_y\end\right.\)
6. При необходимости дополнить решение задачи другими уравнениями.
7. Произвести математические вычисления.

Если в задаче указаны несколько движущихся тел, анализировать силы и записывать системы уравнений необходимо сделать для каждого из них.

Примеры решения задач по динамике

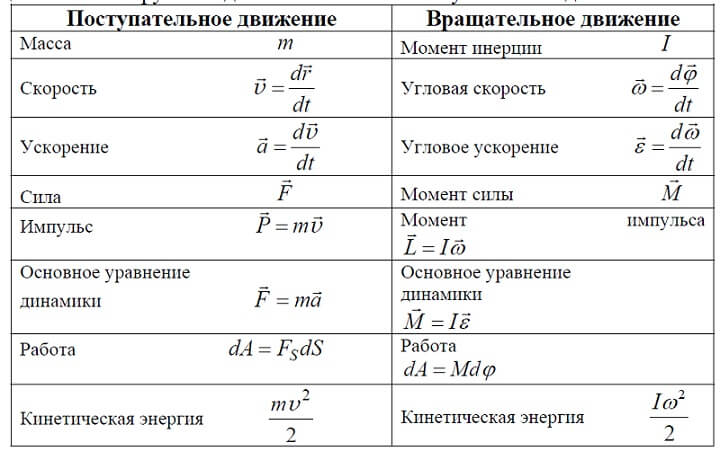
Основные формулы, используемые для решения задач на поступательное и вращательное движение в динамике:

Приведем несколько наглядных примеров решения задач по динамике.

Задачи по динамике поступательного движения с решениями

Задача № 1:

Объект массой 3 килограмма передвигается горизонтально с ускорением, равным \(4 м/с^2\) . Определите силу, действующую на тело.

1. Запишем вводные данные: \(m=3 кг\) , \(a=4 м/с^2, F=?\)
2. Находим силу по формуле, иллюстрирующей второй закон Ньютона: \(F=m\times a.\)
3. Подставляем числовые данные в формулу и получаем ответ: \(12 Н.\)

Задача №2:

Задачи по динамике вращательного движения с решениями

Решение задач на вращательное движение производится при помощи законов Ньютона, также важно помнить основное уравнение динамики вращательного движения:

где \(M\) — момент силы, которая действует на тело, \(J\) — инерция, \(\epsilon\) — угловое ускорение.

Задача:

Задачи по физике могут изрядно испортить настроение, если предмет не нравится, а суть его остается неясной. В таком случае за помощью можно обратиться к образовательному сервису Феникс.Хелп. Наши специалисты с легкостью разбираются в любых темах.

Источник

Задачи по динамике с решениями

• 12 января 2021 г.
• 13 минут
• 33 322

Динамика – раздел механики, которому уделяется больше всего учебных часов. Уделите 5 минут на то, чтобы прочесть нашу статью и чуть больше разобраться в решении задач по динамике.

Наш телеграм – место, где мы скрупулезно отбираем, фильтруем и выкладываем все, что может быть полезно современному студенту. Под лежачий камень вода не течет, подписывайтесь!

Для начала, вопрос. Какой алгоритм решения задач по динамике? Собственно, алгоритм такой же, как и для любой задачи по физике. Мы уже писали об этом в памятке по решению задач. Не забываем держать под рукой полезные формулы, повторяем вопросы из теории, и можно приступать к практическим заданиям.

Вопросы по теме «Динамика»

Вопрос 1. Что изучает динамика?

Ответ. Динамика – раздел механики, который изучает взаимодействия между телами.

Вопрос 2. Каково основное уравнение динамики?

Ответ. Основное уравнение динамики устанавливает связь между приложенной к телу силой, его массой и ускорением тела.

Вопрос 3. Что такое вес тела и зависит ли он от местоположения тела на поверхности Земли?

Ответ. Вес – это сила, с которой тело действует на опору. Вес зависит от ускорения свободного падения, а значит и от географического местоположения на поверхности планеты. А вот масса тела всегда неизменна (за исключением движения со скоростью, близкой к скорости света).

Вопрос 4. В каких системах отсчета справедлив второй закон Ньютона?

Ответ. Второй закон Ньютона справедлив в инерциальных системах отсчета.

Вопрос 5. Сила тяжести на земле является отдельным проявлением одного из фундаментальных физических взаимодействий. Что это за взаимодействие.

Ответ. Конечно, это гравитационное взаимодействие. А сила тяжести – проявление силы всемирного тяготения.

Задачи по динамике поступательного движения с решениями

Задача №1. Определение времени движения

Условие

Тело находится у основания наклонной плоскости с углом при основании α = 30°. Коэффициент трения о поверхность равен µ = 0,6 и масса тела m = 2 кг. Сколько времени тело будет двигаться по наклонной плоскости, если его толкнуть вверх вдоль плоскости со скоростью υ0 = 20 м/с? (g = 9,8 м/с2).

Решение

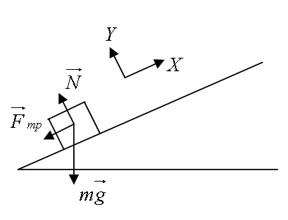
Для начала, выполним рисунок:

Тело будет двигаться равнозамедленно с ускорением, равным –a в течение времени t, при этом

Определим ускорение a. Запишем второй закон Ньютона в векторной форме и в проекциях на оси Х и Y соответственно:

Сила трения определяется выражением

Следовательно, время, в течение которого тело будет двигаться по наклонной плоскости:

Подставим числовые значения:

Ответ: 2 секунды.

Задача №2. Применение второго закона Ньютона

Условие

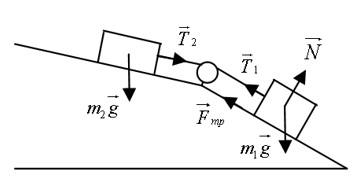
В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30, а верхний брусок – вдоль наклонной плоскости, составляющий с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и наклонной плоскостью равен µ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси, найдите, при каких значениях угла β нить будет растянута.

Решение

Так как тангенс угла α больше, чем коэффициент трения между бруском и поверхностью, нижний брусок будет скользить по наклонной плоскости даже при ненатянутой нити. Следовательно, в том случае, когда оба бруска движутся и нить натянута, модули ускорений брусков будут одинаковыми. Обозначим массу нижнего бруска как m1, массу верхнего бруска как m2, а силу натяжения соединяющей их нити как T. Тогда для каждого из брусков можно записать второй закон Ньютона в проекции на направление его движения:

где Fтр – действующая на нижний брусок сила трения скольжения, N – действующая на него сила нормальной реакции опоры.
Так как нижний брусок не движется в направлении, перпендикулярном плоскости, то из второго закона Ньютона следует:

Решая совместно полученные уравнения, найдем:

Для того, чтобы нить была натянута, должно выполняться неравенство:

С учетом полученного выражения для модуля ускорения a, это неравенство можно переписать в следующем виде:

Подставим числовые значения и найдем искомый угол:

Ответ: 19°.

Задача №3. Нахождение силы

Условие

Два одинаковых груза массой M = 100 г каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой m = 20 г, после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь.

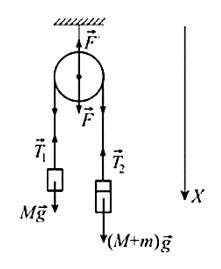
Решение

На основании второго закона Ньютона уравнение движение для обоих грузов с учетом перегрузки на одном из них в проекции на вертикальную ось, направленную вниз, выглядит следующим образом:

где a1 и a2 – проекции ускорений грузов M и (M+m) на вертикальную ось;
T1 и T2 – проекции сил натяжения нити на вертикальную ось. Так как нить не растяжима (по условию задачи), то

Из-за невесомости блока и нити и отсутствия трения, справедливо равенство:

В силу третьего закона Ньютона:

где F с индексом штрих – сила, действующая на блок со стороны его оси. Из первых двух уравнений получим:

Подставим числовые значения:

Ответ: 2,14 Ньютона.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Задачи по динамике вращательного движения с решениями

Задача №4. Нахождение числа оборотов маховика

Условие

Маховик радиусом R=0,5 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно Т=98 Н. Какое число оборотов в секунду будет делать маховик через Δt=10 с после начала движения. Маховик считать однородным диском.

Решение

Основное уравнение динамики вращательного движения:

где J — момент инерции маховика. Принимая маховик за однородный диск, можно записать:

Момент силы натяжения ремня:

Угловое ускорение маховика:

Угловая скорость маховика:

Решая уравнения, записанные выше, получим ответ:

Ответ: 62,4 оборота в секунду

Задача №5. Нахождение углового ускорения

Условие

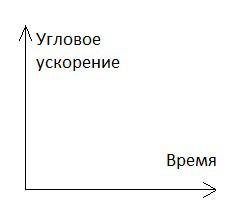
Момент силы, приложенный к вращающемуся телу изменяется по закону M=M0-αt. Момент остаётся постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке. Найти выражение для углового ускорения.

Решение

Согласно основному закону динамики вращательного движения:

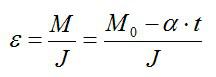
Это уравнение прямой с отрицательным углом наклона, что соответствует рисунку.

Нужна помощь в решении задач по динамике, теоретической механике, деталям машин, химии, etc? Обращайтесь за ней в профессиональный студенческий сервис.

Источник