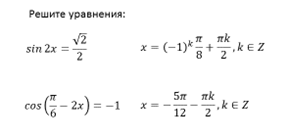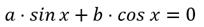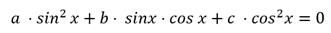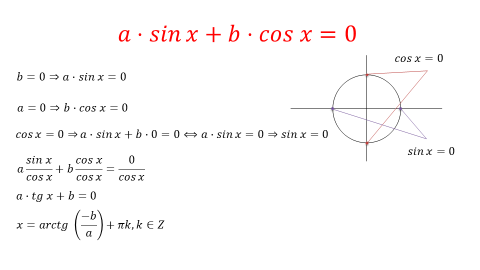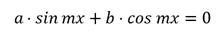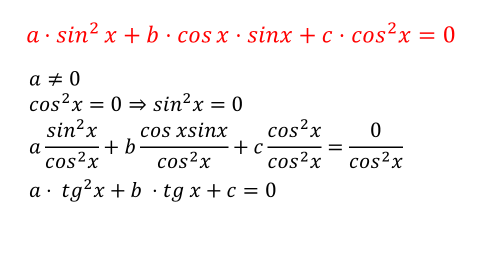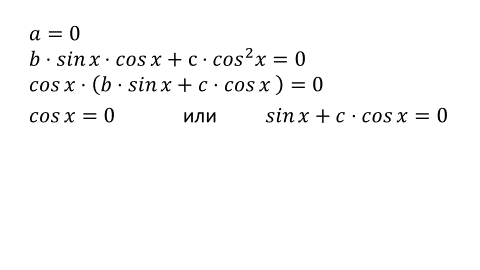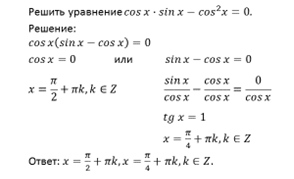Способы решения тригонометрических уравнений решение однородных уравнений

Методы решения тригонометрических уравнений.

1. Алгебраический метод.

( метод замены переменной и подстановки ).

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Источник

Однородные тригонометрические уравнения

Урок 24. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Однородные тригонометрические уравнения»

· познакомиться с понятием «однородные тригонометрические уравнения»;

· рассмотреть способы решения однородных тригонометрических уравнений.

Мы продолжаем с вами изучать тему «Тригонометрические уравнения» и сегодня на уроке познакомимся ещё с некоторыми уравнениями и определимся с методами для их решения.

Но прежде чем перейти к изучению нового материала, выполните упражнение.

На практике довольно часто встречаются тригонометрические уравнения вида

Или уравнения вида

Уравнения такого вида называют однородными тригонометрическими уравнениями.

Итак, рассмотрим однородные уравнения первой степени.

С помощью деления на одну из тригонометрических функций решаются и однородные тригонометрические уравнения первой степени вида

Только делить мы будем не на cos x, а на cos mx.

Рассмотрим теперь однородное тригонометрическое уравнение второй степени.

Теперь давайте рассмотрим случай, когда в однородном тригонометрическом уравнении отсутствует слагаемое, содержащее синус квадрат, то есть коэффициент а равен нулю.

Аналогично решаются однородные уравнения второй степени, у которых отсутствует слагаемое косинус квадрат x.

Давайте, объединим все рассмотренные случаи и составим единый алгоритм решения однородного тригонометрического уравнения второй степени в общем виде.

Источник

Однородные уравнения (ЕГЭ 2022)

В этой статье ты научишься решать однородные уравнения.

В частности, тригонометрические и показательные.

И это не так сложно, как выглядит!

Потому что алгоритм решения однородных уравнений один и тот же!

Для этого эти уравнения и выделили в одну группу – чтобы было легче решать. По одному алгоритму.

Читай статью, решай примеры и все поймешь!

Однородные уравнения — коротко о главном

Определение однородных уравнений

Однородные уравнения – это уравнения вида \( <_<0>><^>+<_<1>><^>y+<_<2>><^><^<2>>+…+<_>x<^>+<_><^>=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.

Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.

Алгоритм решения однородных уравнений

Однородные уравнение — подробнее

Что такое однородные уравнения? Давай посмотрим на определение.

Однородные уравнения – это уравнения вида \( <_<0>><^>+<_<1>><^>y+<_<2>><^><^<2>>+…+<_>x<^>+<_><^>=0\) с двумя неизвестными, в каждом из слагаемых которых одинаковая сумма степеней этих неизвестных.

Совершенно пугающее определение, поэтому разберемся на примере.

Пример №1

Это уравнение однородное. Почему? Давай посмотрим на определение.

Стоп! Давай все-таки попытаемся разобраться в этой громоздкой формуле.

На первом месте должна идти первая переменная в степени \( n\) с некоторым коэффициентом. В нашем случае это \( 1\cdot <^<2>>,\ \ k=1,\ \ x=a,\ \ n=2\)

Дальше идет первая переменная в степени \( n-1\) и вторая переменная в первой степени.

В нашем случае это \( -4ab\).

Как мы выяснили, \( n=2\), значит здесь степень \( n-1=1\) при первой переменной \( \left( a \right)\) – сходится.

И вторая переменная \( \left( b \right)\) в первой степени – на месте. Коэффициент \( k=\)\( -4\).

Первая переменная \( \left( a \right)\) в степени \( n-2=0\), и вторая переменная \( \left( b \right)\) в квадрате, с коэффициентом \( \left( 3 \right)\). Это последний член уравнения.

Как видишь, наше уравнение подходит под определение в виде формулы.

Давай рассмотрим вторую (словесную) часть определения.

…с двумя неизвестными, в каждом из слагаемых которого одинаковая сумма степеней этих неизвестных.

У нас две неизвестные \( (a\) и \( b)\). Здесь сходится.

Рассмотрим все слагаемые. В них сумма степеней неизвестных должна быть одинакова.

\( -4ab\) — сумма степеней равна \( 2\) (\( 1\) при \( a\) и \( 1\) при \( b\)).

\( 3<^<2>>\) — сумма степеней равна \( 2\).

Как видишь, все сходится! Это однородное уравнение.

Теперь давай потренируемся в определении однородных уравнений.

Определи какие из уравнений — однородные

Однородные уравнения — уравнения под номерами:

Рассмотрим отдельно \( 11\) уравнение.

Если мы разделим каждое слагаемое на разложим каждое слагаемое, то получим:

А это уравнение полностью попадает под определение однородных уравнений.

Как решать однородные уравнения

Решение всех однородных уравнений сводится к делению на одну из неизвестных в степени \( n\) и дальнейшей заменой переменных.

Пример №2

Найдите \( \displaystyle \frac\).

Разделим уравнение на \( <^<2>>\).

Нужно всегда помнить, что делить (и умножать) на переменную мы можем только тогда, когда мы уверены, что эта переменная не может быть равна \( 0\). Например, если нас просят найти \( \frac\), то мы сразу понимаем, что \( y\ne 0\), поскольку на \( 0\) делить нельзя.

Когда это не так очевидно, необходимо отдельно проверять случай, когда эта переменная равна \( 0\).

У нас по условию y не может быть равен \( 0\). Поэтому мы можем смело делить на \( <^<2>>\)

Произведя замену \( t=\frac\), мы получим простое квадратное уравнение:

Так как это приведенное квадратное уравнение, воспользуемся теоремой Виета:

Произведя обратную замену, получаем ответ

Ответ: \( 2;5\)

Пример №3

Нужно найти: \( \displaystyle \ \frac.\)

Решение:

Разделим уравнение на \( <^<2>>\) (\( y\ne 0\) по условию).

Произведем замену \( \displaystyle t=\frac\) и решим квадратное уравнение:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Пример №4

Здесь нужно не делить, а умножать.

Умножим все уравнение на \( <^<2>>\):

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Решение однородных тригонометрических уравнений

Решение однородных тригонометрических уравнений ничем не отличается от способов решения, описанных выше.

Только здесь, помимо прочего, нужно немного знать тригонометрию. И уметь решать тригонометрические уравнения (для этого можешь прочитать раздел «Тригонометрические уравнения»).

Рассмотрим такие уравнения на примерах.

Пример №5

Решите уравнение \( <<\sin >^<2>>x-3\sin x\cdot \cos x-4<<\cos >^<2>>x=0\).

Мы видим типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).

Подобные однородные уравнения решаются не сложно, но перед тем, как разделить уравнения на \( <<\cos >^<2>>x\), рассмотрим случай, когда \( \cos x=0\)

В этом случае уравнение примет вид: \( <<\sin >^<2>>x=0\), значит \( \sin x=0\). Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\). Поэтому \( \cos x\ne 0\), и на него можно смело делить:

Сделаем замену \( t=tgx\) и решим квадратное уравнение:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Пример №6

Решите уравнение \( 5<<\sin >^<2>>x-2\sin x\cdot \cos x-3<<\cos >^<2>>x=0\).

Как и в примере \( 5\), нужно разделить уравнение на \( <<\cos >^<2>>x\).

Рассмотрим случай, когда \( \cos x=0\) :

Но синус и косинус не могут одновременно быть равны \( 0\), ведь по основному тригонометрическому тождеству \( <<\cos >^<2>>x+<<\sin >^<2>>x=1\).

Поэтому \( \cos x\ne 0\).

Сделаем замену \( t=tgx\) и решим квадратное уравнение:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Решение однородных показательных уравнений

Однородные уравнения решаются так же, как рассмотренных выше. Если ты забыл, как решать показательные уравнения – посмотри соответствующий раздел («Показательные уравнения»)!

Рассмотрим несколько примеров.

Пример №7

Мы видим типичное однородное уравнение, с двумя переменными и суммой степеней \( 2x\). Разделим уравнение на \( <<18>^<2x>>\):

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Пример №8

Разделим уравнение на \( <<16>^<2x>>\):

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Пример №9

На примере этой задачи повторим, что такое однородные уравнения и как их решать.

Здесь можно заметить любопытную вещь: если поделить каждое слагаемое на \( <^<2>>\), получим:

То есть, теперь нет отдельных \( a\) и \( b\), – теперь переменной в уравнении является искомая величина \( \frac\). И это обычное квадратное уравнение, которое легко решить с помощью теоремы Виета: произведение корней равно \( 2\), а сумма \( 3\) – это числа \( 2\) и \( 1\).

Ответ: \( 1;\text< >2.\)

называется однородным.

То есть это уравнение с двумя неизвестными, в каждом слагаемом которого одинаковая сумма степеней этих неизвестных. Например, в примере выше эта сумма равна \( 2\).

Решение однородных уравнений осуществляется делением на одну из неизвестных в этой степени:

И последующей заменой переменных: \( t=\frac\). Таким образом получаем уравнение \( n\) степени с одной неизвестной \( t\):

Чаще всего нам будут встречаться уравнения второй степени (то есть квадратные), а их решать мы умеем:

\( \displaystyle \Leftrightarrow\ a<^<2>>+bt+c=0\).

Отметим, что делить (и умножать) все уравнение на переменную можно только если мы убеждены, что эта переменная не может быть равна нулю!

Например, если нас просят найти \( \displaystyle \frac\), сразу понимаем, что \( y\ne 0\), поскольку на \( 0\) делить нельзя.

В случаях, когда это не так очевидно, необходимо отдельно проверять случай когда эта переменная равна нулю. Например:

Решите уравнение \( <<\sin >^<2>>x+3\sin x\cdot \cos x+2<<\cos >^<2>>x=0\).

Пример №10

Видим здесь типичное однородное уравнение: \( \sin x\) и \( \cos x\) – это неизвестные, а сумма их степеней в каждом слагаемом равна \( 2\).

Но, прежде чем разделить на \( <<\cos >^<2>>x\) и получить квадратное уравнение относительно \( \displaystyle \frac<\sin x><\cos x>\), мы должны рассмотреть случай, когда \( \cos x=0\).

Источник