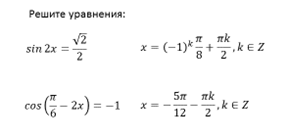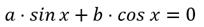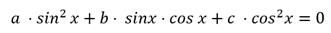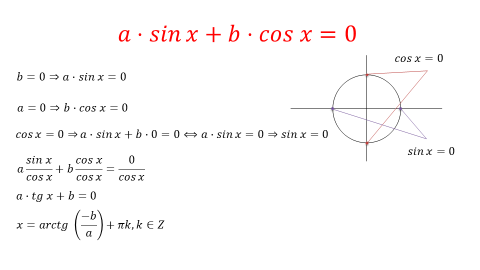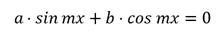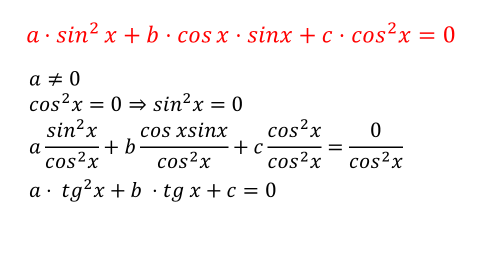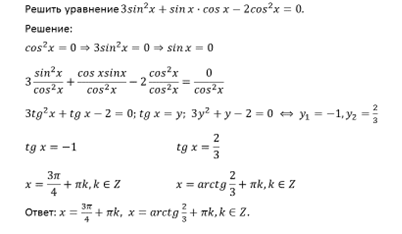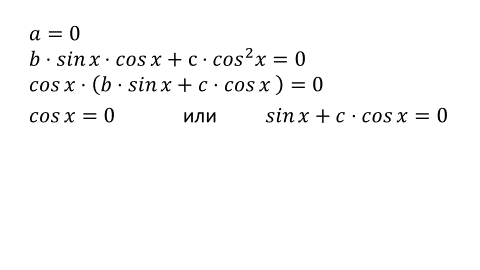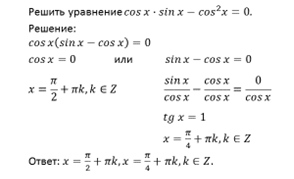- Способы решения тригонометрических уравнений однородные уравнения
- Методы решения тригонометрических уравнений.
- 1. Алгебраический метод.
- 2. Разложение на множители.
- 3. Приведение к однородному уравнению.
- 4. Переход к половинному углу.
- 5. Введение вспомогательного угла.
- 6. Преобразование произведения в сумму.
- Однородные тригонометрические уравнения
- Урок 24. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Однородные тригонометрические уравнения»
- Однородные тригонометрические уравнения: общая схема решения
- Алгоритм решения
- Выделим слагаемые
- Используем формулу основного тригонометрического тождества и записываем окончательное решение
- Решаем реальные задачи
- Задача №1
- Задача №2
- Задача №3
- Полезные советы
- Ключевые моменты
- Общая схема решения
Способы решения тригонометрических уравнений однородные уравнения
Методы решения тригонометрических уравнений.
1. Алгебраический метод.
( метод замены переменной и подстановки ).
2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е . Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
3. Приведение к однородному уравнению.
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
cos ( или sin ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно tan .
П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда
1) tan x = –1, 2) tan x = –3,
4. Переход к половинному углу.
П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
5. Введение вспомогательного угла.
где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos 


6. Преобразование произведения в сумму.
П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .
Р е ш е н и е . Преобразуем левую часть в сумму:
Источник
Однородные тригонометрические уравнения
Урок 24. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Однородные тригонометрические уравнения»
· познакомиться с понятием «однородные тригонометрические уравнения»;
· рассмотреть способы решения однородных тригонометрических уравнений.
Мы продолжаем с вами изучать тему «Тригонометрические уравнения» и сегодня на уроке познакомимся ещё с некоторыми уравнениями и определимся с методами для их решения.
Но прежде чем перейти к изучению нового материала, выполните упражнение.
На практике довольно часто встречаются тригонометрические уравнения вида
Или уравнения вида
Уравнения такого вида называют однородными тригонометрическими уравнениями.
Итак, рассмотрим однородные уравнения первой степени.
С помощью деления на одну из тригонометрических функций решаются и однородные тригонометрические уравнения первой степени вида
Только делить мы будем не на cos x, а на cos mx.
Рассмотрим теперь однородное тригонометрическое уравнение второй степени.
Теперь давайте рассмотрим случай, когда в однородном тригонометрическом уравнении отсутствует слагаемое, содержащее синус квадрат, то есть коэффициент а равен нулю.
Аналогично решаются однородные уравнения второй степени, у которых отсутствует слагаемое косинус квадрат x.
Давайте, объединим все рассмотренные случаи и составим единый алгоритм решения однородного тригонометрического уравнения второй степени в общем виде.
Источник
Однородные тригонометрические уравнения: общая схема решения
15 сентября 2013
Сегодня мы займемся однородными тригонометрическими уравнениями. Для начала разберемся с терминологией: что такое однородное тригонометрическое уравнение. Оно имеет следующие характеристики:
- в нем должно быть несколько слагаемых;
- все слагаемые должны иметь одинаковую степень;
- все функции, входящие в однородное тригонометрическое тождество, должны обязательно иметь одинаковый аргумент.
Алгоритм решения
Выделим слагаемые
И если с первым пунктом все понятно, то о втором стоить поговорить поподробней. Что значит одинаковая степень слагаемых? Давайте рассмотрим первую задачу:
Первое слагаемое в этом уравнении — 3cosx 3\cos x. Обратите внимание, здесь есть только одна тригонометрическая функция — cosx \cos x — и больше никаких других тригонометрических функций здесь не присутствует, поэтому степень этого слагаемого равна 1. То же самое со вторым — 5sinx 5\sin x — здесь присутствует только синус, т. е. степень этого слагаемого тоже равна единице. Итак, перед нами тождество, состоящее из двух элементов, каждое из которых содержит тригонометрическую функцию, и при этом только одну. Это уравнение первой степени.
Переходим ко второму выражению:
4 sin 2 x+sin2x−3=0
Первый член этой конструкции — 4 sin 2 x 4<<\sin >^<2>>x.
Теперь мы можем записать следующее решение:
sin 2 x=sinx⋅sinx
Другими словами, первое слагаемое содержит две тригонометрические функции, т. е. его степень равна двум. Разберемся со вторым элементом — sin2x \sin 2x. Вспомним такую формулу — формулу двойного угла:
\sin 2x=2\sin x\cdot \cos x
И опять, в полученной формуле у нас есть две тригонометрические функции — синус и косинус. Таким образом, степенное значение этого члена конструкции тоже равно двум.
Переходим к третьему элементу — 3. Из курса математики средней школы мы помним, что любое число можно умножать на 1, так и запишем:
А единицу с помощью основного тригонометрического тождества можно записать в следующем виде:
1= sin 2 x⋅ cos 2 x
Следовательно, мы можем переписать 3 в следующем виде:
3=3 ( sin 2 x⋅ cos 2 x ) =3 sin 2 x+3 cos 2 x
Таким образом, наше слагаемое 3 разбилось на два элемента, каждый из которых является однородным и имеет вторую степень. Синус в первом члене встречается дважды, косинус во втором — тоже дважды. Таким образом, 3 тоже может быть представлено в виде слагаемого со степенным показателем два.
С третьим выражением то же самое:
sin 3 x+ sin 2 xcosx=2 cos 3 x
Давайте посмотрим. Первое слагаемое — sin 3 x <<\sin >^<3>>x — это тригонометрическая функция третьей степени. Второй элемент — sin 2 xcosx <<\sin >^<2>>x\cos x.
sin 2 <<\sin >^<2>> — это звено со степенным значением два, умноженное на cosx \cos x — слагаемое первой. Итого, третий член тоже имеет степенное значение три. Наконец, справа стоит еще одно звено — 2 cos 3 x 2<<\cos >^<3>>x — это элемент третьей степени. Таким образом, перед нами однородное тригонометрическое уравнение третьей степени.
У нас записано три тождества разных степеней. Обратите внимание еще раз на второе выражение. В исходной записи у одного из членов присутствует аргумент 2x 2x. Мы вынуждены избавиться от этого аргумента, преобразовав его по формуле синуса двойного угла, потому что все функции, входящие в наше тождество, должны обязательно иметь одинаковый аргумент. И это требование для однородных тригонометрических уравнений.
Используем формулу основного тригонометрического тождества и записываем окончательное решение
С терминами мы разобрались, переходим к решению. Независимо от степенного показателя, решение равенств такого типа всегда выполняется в два шага:
\cos x\ne 0. Для этого достаточно вспомнить формулу основного тригонометрического тождества ( sin 2 x⋅ cos 2 x=1 ) \left( <<\sin >^<2>>x\cdot <<\cos >^<2>>x=1 \right) и подставить в эту формулу cosx=0 \cos x=0. Мы получим следующее выражение:
Подставляя полученные значения, т. е. вместо cosx \cos x — ноль, а вместо sinx \sin x — 1 или -1, в исходное выражение, мы получим неверное числовое равенство. Это и является обоснованием того, что
2) второй шаг логичным образом вытекает из первого. Поскольку
\cos x\ne 0, делим обе наши стороны конструкции на cos n x <<\cos >^
\[\begin
Благодаря этому наша громоздкая исходная конструкция сводится к уравнению n n-степени относительно тангенса, решение которой легко записать с помощью замены переменной. Вот и весь алгоритм. Давайте посмотрим, как он работает на практике.
Решаем реальные задачи
Задача №1
Мы уже выяснили, что это однородное тригонометрическое уравнение со степенным показателем, равным единице. Поэтому в первую очередь выясним, что cosx≠0 \cos x\ne 0. Предположим противное, что
\cos x=0\to \sin x=\pm 1.
Подставляем полученное значение в наше выражение, получаем:
\begin
На основании этого можно сказать, что cosx≠0 \cos x\ne 0. Разделим наше уравнение на cosx \cos x, потому что все наше выражение имеет степенное значение, равное единице. Получим:
3 ( cosx cosx ) +5 ( sinx cosx ) =0 3+5tg x=0 tg x=− 3 5
Это не табличное значение, поэтому в ответе будет фигурировать arctg x arctgx:
x=arctg ( − 3 5 ) + π n,n∈Z
x=arctg\left( -\frac<3> <5>\right)+\text< >\!\!\pi\!\!\text< >n,n\in Z
Поскольку arctg arctg arctg— функция нечетная, «минус» мы можем вынести из аргумента и поставить его перед arctg. Получим окончательный ответ:
x=−arctg 3 5 + π n,n∈Z
Задача №2
4 sin 2 x+sin2x−3=0
Как вы помните, прежде чем приступить к его решению, нужно выполнить некоторые преобразования. Выполняем преобразования:
4 sin 2 x+2sinxcosx−3 ( sin 2 x+ cos 2 x ) =0 4 sin 2 x+2sinxcosx−3 sin 2 x−3 cos 2 x=0 sin 2 x+2sinxcosx−3 cos 2 x=0
Мы получили конструкцию, состоящую из трех элементов. В первом члене мы видим sin 2 <<\sin >^<2>>, т. е. его степенное значение равно двум. Во втором слагаемом мы видим sinx \sin x и cosx \cos x — опять же функции две, они перемножаются, поэтому общая степень снова два. В третьем звене мы видим cos 2 x <<\cos >^<2>>x — аналогично первому значению.
Докажем, что cosx=0 \cos x=0 не является решением данной конструкции. Для этого предположим противное:
\[\begin
Мы доказали, что cosx=0 \cos x=0 не может быть решением. Переходим ко второму шагу — делим все наше выражение на cos 2 x <<\cos >^<2>>x. Почему в квадрате? Потому что степенной показатель этого однородного уравнения равен двум:
sin 2 x cos 2 x +2 sinxcosx cos 2 x −3=0 t g 2 x+2tg x−3=0
Можно ли решать данное выражение с помощью дискриминанта? Конечно можно. Но я предлагаю вспомнить теорему, обратную теореме Виета, и мы получим, что данный многочлен представим в виде двух простых многочленов, а именно:
(tg x+3) (tg x−1) =0 tg x=−3→x=−arctg 3+ π n,n∈Z tg x=1→x= π 4 + π k,k∈Z
\begin
Многие ученики спрашивают, стоит ли для каждой группы решений тождеств писать отдельные коэффициенты или не заморачиваться и везде писать один и тот же. Лично я считаю, что лучше и надежнее использовать разные буквы, чтобы в случае, когда вы будете поступать в серьезный технический вуз с дополнительными испытаниями по математике, проверяющие не придрались к ответу.
Задача №3
sin 3 x+ sin 2 xcosx=2 cos 3 x
Мы уже знаем, что это однородное тригонометрическое уравнение третьей степени, никакие специальные формулы не нужны, и все, что от нас требуется, это перенести слагаемое 2 cos 3 x 2<<\cos >^<3>>x влево. Переписываем:
sin 3 x+ sin 2 xcosx−2 cos 3 x=0
Мы видим, что каждый элемент содержит в себе три тригонометрические функции, поэтому это уравнение имеет степенное значение, равное трем. Решаем его. В первую очередь, нам нужно доказать, что cosx=0 \cos x=0 не является корнем:
Подставим эти числа в нашу исходную конструкцию:
(±1) 3 +1⋅0−2⋅0=0 ±1+0−0=0 ±1=0
Следовательно, cosx=0 \cos x=0 не является решением. Мы доказали, что cosx≠0 \cos x\ne 0. Теперь, когда мы это доказали, разделим наше исходное уравнение на cos 3 x <<\cos >^<3>>x. Почему именно в кубе? Потому что мы только что доказали, что наше исходное уравнение имеет третью степень:
sin 3 x cos 3 x + sin 2 xcosx cos 3 x −2=0 t g 3 x+t g 2 x−2=0
Введем новую переменную:
Перед нами кубическое уравнение. Как его решать? Изначально, когда я только составлял данный видеоурок, то планировал предварительно рассказать о разложении многочленов на множители и прочих приемов. Но в данном случае все намного проще. Взгляните, наше тождество приведенное, при слагаемом с наибольшей степенью стоит 1. Кроме того, все коэффициенты целые. А это значит, что мы можем воспользоваться следствием из теоремы Безу, которое гласит, что все корни являются делителями числа -2, т. е. свободного члена.
Возникает вопрос: на что делится -2. Поскольку 2 — число простое, то вариантов не так уж много. Это могут быть следующие числа: 1; 2; -1; -2. Отрицательные корни сразу отпадают. Почему? Потому что оба они по модулю больше 0, следовательно, t 3 <
˜t=1\to \text< >1+1-2=0\to 0=0
Мы получили верное числовое равенство. Следовательно, t=1 t=1 является корнем.
t=2\to 8+4-2=0\to 10\ne 0
t=2 t=2 не является корнем.
Согласно следствию и все той же теореме Безу, любой многочлен, чьим корнем является x 0 <
В нашем случае в роли x x выступает переменная t t, а в роли x 0 <
t 3 + t 2 −2=(t−1)⋅P (t)
Как найти многочлен P (t) P\left( t \right)? Очевидно, нужно сделать следующее:
P (t)= t 3 + t 2 −2 t−1
t 3 + t 2 +0⋅t−2 t−1 = t 2 +2t+2
Итак, наш исходный многочлен разделился без остатка. Таким образом, мы можем переписать наше исходное равенство в виде:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Первый множитель мы уже рассмотрели. Давайте рассмотрим второй:
Опытные ученики, наверное, уже поняли, что данная конструкция не имеет корней, но давайте все-таки посчитаем дискриминант.
Дискриминант меньше 0, следовательно, выражение не имеет корней. Итого, огромная конструкция свелась к обычному равенству:
Полезные советы
В заключение хотелось бы добавить пару замечаний по последней задаче:
- всегда ли будет выполняться условие cosx≠0 \cos x\ne 0,и стоит ли вообще проводить эту проверку. Разумеется, не всегда. В тех случаях, когда cosx=0 \cos x=0 является решением нашего равенства, следует вынести его за скобки, и тогда в скобках останется полноценное однородное уравнение.
- что такое деление многочлена на многочлен. Действительно, в большинстве школ этого не изучают, и когда ученики впервые видят такую конструкцию, то испытывают легкий шок. Но, на самом деле, это простой и красивый прием, который существенно облегчает решение уравнений высших степеней. Разумеется, ему будет посвящен отдельный видеоурок, который я опубликую в ближайшее время.
Ключевые моменты
Однородные тригонометрические уравнения — любимая тема на всевозможных контрольных работах. Решаются они очень просто — достаточно один раз потренироваться. Чтобы было понятно, о чем речь, введем новое определение.
Однородное тригонометрическое уравнение — это такое, в котором каждое ненулевое слагаемое которого состоит из одинакового количества тригонометрических множителей. Это могут быть синусы, косинусы или их комбинации — метод решения всегда один и тот же.
Степень однородного тригонометрического уравнения — это количество тригонометрических множителей, входящих в ненулевые слагаемые.Примеры:
\sin x+15\text< cos >x=0 — тождество 1-й степени;
2\text< sin>2x+5\sin xcosx-8\cos 2x=0 — 2-й степени;
\sin 3x+2\sin x\cos 2x=0 — 3-ей степени;
\sin x+\cos x=1 — а это уравнение не является однородным, поскольку справа стоит единица — ненулевое слагаемое, в котором отсутствуют тригонометрические множители;
\sin 2x+2\sin x-3=0 — тоже неоднородное уравнение. Элемент sin2x \sin 2x — второй степени (т.к. можно представить
\sin 2x=2\sin x\cos x), 2sinx 2\sin x — первой, а слагаемое 3 — вообще нулевой, поскольку ни синусов, ни косинусов в нем нет.
Общая схема решения
Схема решения всегда одна и та же:
Предположим, что cosx=0 \cos x=0. Тогда sinx=±1 \sin x=\pm 1 — это следует из основного тождества. Подставляем sinx \sin x и cosx \cos x в исходное выражение, и если получается бред (например, выражение 5=0 5=0), переходим ко второму пункту;
Делим все на степень косинуса: cosx,cos2x,cos3x. — зависит от степенного значения уравнения. Получим обычное равенство с тангенсами, которое благополучно решается после замены tg x=t.
tgx=tНайденные корни будут ответом к исходному выражению.
Источник