Старинные задачи и способы их решения
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Содержимое разработки

Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А меня очень заинтересовали старинные задачи, с которыми мы столкнулись на уроке математики. И я решил узнать о них больше. Старинные задачи пришли к нам из глубины веков, от наших предков. Разные народы нашей планеты придумывали их, оттачивали условия и логику заданий. Они неизбежно остроумны и занимательны, в них собраны замечательные находки многих поколений.
Старинные задачи позволяют не только развить смекалку и сообразительность, но и почувствовать прикосновение других эпох, порадоваться пришедшему решению точно так же, как когда-то, быть может, радовались наши предки. Наши предки умели думать и решать задачи. Очень многие сказки воспевают смекалку и скорость мышления, благодаря которым герои обретают счастье. Такие качества, как сообразительность, оригинальность слова и дела, уникальность и мастерство всегда были и будут в цене. Конечно, задач и головоломок за века было придумано неисчислимое множество, и я специально отобрал лучшие из них.
Еще в древние века математика занимала основное место в умах ученых и благодаря сохранившимся рукописям у нас есть возможность проследить за развитием математической мысли и возможность прорешать старинные задачи и сравнить их решение с современным решением.
Цель исследования: выявление роли и места старинных задач в современном мире, рассмотрение различных способов решения старинных задач.
- исследовать решение старинных задач методом перебора; методом подбора; методом предположения, алгебраическим способом; наглядно-геометрическим способом
- исследовать старинный способ решения задач на сплавы и смеси.
Диофант умел решать
очень сложные уравнения,
он применял для этого
Жизнь Диофанта . По преданию, на могильном камне имелась такая надпись:
«Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую- юношей, седьмую- провёл неженатым. Через 5 лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько прожил Диофант?»





Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты. При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве). Существует старинный способ решения задач на смеси и сплавы. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Л.Ф.Магницкого.
После определения числового выражения — переход на следующий слайд (верхняя кнопка)
Попадая повторно на этот слайд повторяем определение буквенных выражений. Далее: Чтобы получить второе определение – нажмите на «Знайку». После определения буквенных выражений нажмите на вторую кнопу и Вы перейдете к практическому заданию.
Лео́нтий Фили́ппович Магни́цкий (9(19)июня 1669- 19(30)октября 1739)
Магницкий Л.Ф. (при рождении Телятин)-
русский математик, педагог;
преподаватель математики в Школе
математических и навигацких наук
в Москве (с 1701 по 1739),
автор первой в России учебной
энциклопедии по математике
(в 1703г. «Арифметика»), которая
более ста лет являлась основным
учебным пособием по математике
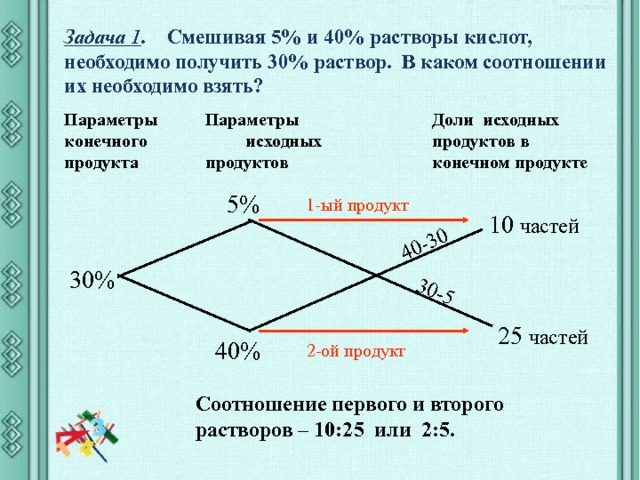
Задача 1 . Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?
Параметры конечного продукта
Параметры исходных продуктов
Доли исходных продуктов в конечном продукте
Соотношение первого и второго растворов – 10:25 или 2:5.
Задача 1а. Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. Сколько грамм каждой кислоты необходимо смешать, чтобы получить 140 г 30%- ого раствора?
- Сколько грамм приходится на одну часть?
- Сколько грамм 5%-го раствора взять?
- Сколько грамм 40%-го раствора взять?
Ответ: для получения 140г 30%-ного раствора нужно
взять 5%-ного раствора 40г, а 40%-ного — 100 г.
Математика в настоящее время все шире проникает в повседневную жизнь, все более внедряется в традиционно далекие от нее области. Компьютеризация общества, внедрение современных информационных технологий требует математической грамотности человека почти на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
Решение задач различными способами способствует углублению знаний, логического мышления, расширяет кругозор.
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (А. Маркушевич)
Ознакомление с историческими фактами позволяет лучше понять роль математики в современном обществе, углубляют понимание изучаемого раздела программы.
В результате изученной темы было выяснено, что существует множество методов различных старинных задач. Естественно, все их виды рассмотреть невозможно. Также мы научились правильно анализировать задачи и решать их разными методами (путём составления уравнений, т.е методом ложного положения, методом полного перебора вариантов и т.д) и разными способами: алгебраическим и арифметическим (старинным). Арифметические способы решения текстовых задач имеют больший развивающий потенциал, чем универсальный алгебраический способ решения. В наше время предпочтение отдаётся алгебраическому способу.
Источник
Способы решения старинных математических задач
Математика предмет очень интересный, но не простой. Не всем людям он дается одинаково. Некоторым дается очень легко, кому – то труднее, а кто — то совсем не умеет решать задачи. А как у вас дела с математикой? Чтобы ответить на этот вопрос проверим вашу логику. Свою работу я хочу начать с задачи- загадки.
Шла баба в Москву и повстречала 3 мужиков. Каждый из них нёс по мешку, в каждом мешке по коту. Сколько существ направлялось в Москву?
Удивительно то, что подобные задачи встречаются в совершенно разных источниках: в папирусах египтянина Ахмеса, у Леонарда Пизанского и в «Школьной арифметике» Даниэля Адамса совсем немного измененные. Значительные преимущества имеет математика перед другими предметами, потому что изучать ее, заниматься ею можно с ранних лет. Многие открытия в математике были сделаны, да и сейчас делаются людьми, еще очень молодыми, не достигшими тридцати, а иногда и двадцати лет.
Выбрана тема о старинных задачах, потому что они показались мне труднее тех, которые мы решаем на уроках. Чтобы справиться с ними, надо проявить сообразительность, смекалку, так как обычных методов тут может и не хватить. Необходимы настойчивость и целеустремленность, без этих качеств нельзя добиться успеха в любом деле, не только в математике.
Цель работы: выбор более удобного способа решения математических задач.
1. Познакомиться с занимательными старинными задачами;
2. Сравнить «старые» и «новые» способы решения задач;
3. Научиться применять в жизненных ситуациях простые арифметические решения.
1. Найти старинные задачи.
2. Узнать способ их решения по-старинному, без букв.
3. Перевести с родного языка на алгебраический.
4. Сравнить эти способы решения.
5. Сделать выводы.
1.Задачи Ахмеса и подобные задачи на Руси.
В древнейших рукописях египтян (около 4 тысяч лет) сохранился папирус Ахмеса. В нём даются решения боле 80 задач на различные вычисления, которые могут понадобиться на практике. Некоторые из этих задач показались бы довольно сложными ученику- старшекласснику нашей школы. Представляете себе, как трудно было их решить 4 тысячи лет назад! Ведь у древних египтян не было ни удобного способа записи чисел, ни наших правил арифметических действий, ни таблицы умножения. Большая часть задач папируса Ахмеса относится к арифметике: задачи на арифметические действия, на пропорциональное деление и т. д. При этом сгруппированы они не по математическому содержанию, а по тому, о чём в них идёт речь.
В Древнем Египте ещё не знали и не подозревали о том, что неизвестные числа можно обозначать буквами, а потом работать с ними как с известными величинами. С дробями у них тоже были сложности. Однако египтяне придумали метод решения таких задач, который назвали «методом кучи».
В папирусе Ахмеса предлагается задача, имеющая отвлечённый характер. Например:В доме 7 кошек, каждая кошка съедает 7 мышей, каждая мышь съедает 7 колосьев, каждый колос даёт 7 растений, на каждом растении 7 мер зерна. Сколько всех вместе?Тут интересно, что в задаче надо ответить на вопрос: сколько всех вместе? Автора задачи не интересует, о каких вещах или предметах идёт речь, однородны они или разнородны,- важно только их общее количество. Значит, очень давно египтяне уже представляли себе не число кошек, или колосьев, или мышей, а именно само по себе число. Но ведь это совсем не так просто. Некоторые задачи были не слишком сложны, но вели к интересным выводам. Такова задача, о которой я сказала только что. В ней надо сосчитать сумму пяти чисел, из которых каждое следующее в 7 раз больше предыдущего. Чтобы решить её, надо было только терпеливо умножать на 7 и складывать.
В XIII веке итальянский математик Леонардо Пизанский, по прозвищу Фибоначчи, привёл в своей книге задачу очень похожую на задачу Ахмеса. Вот ее содержание. Семь старух отправились в Рим. У каждой старухи по семи ослов, каждый осёл несет по семи мешков, в каждом мешке по семи хлебов, в каждом хлебе по семи ножей, каждый нож в семи ножнах. Сколько всего предметов? От задачи Ахмеса она отличается добавлением одного слагаемого.
На Руси также решались похожие задачи. Ещё в XIX веке очень популярной была задача, которую и сейчас загадывают нередко.
«Шли семь старцев.
У каждого старца по семи костылей.
На каждом костыле по семи сучков.
На каждомсучке по семи кошелей.
В каждом кошеле по семи пирогов.
В каждом пирогепо семи воробьёв.
А ведь это та же задача Ахмеса! Прошли тысячи лет, а задачу до сих пор решают. Но такие суммы теперь часто встречаются и получили особое название: сумма геометрической прогрессии и каждый девятиклассник без труда и очень быстро решит ее.
Если сравнить их решения, вы увидите, что современное решение гораздо короче и легче, так как в нем используют формулу и вместо 15 действий, выполняют всего 5. Убедитесь сами.
Старинное решение задач:
7 + 7*7 + 7*7*7 + 7*7*7*7+7*7*7*7*7 =19607.
Современное решение задач:
по формуле суммы первых 5 членов геометрической прогрессии:
7 – 1 Ответ: всех вместе 19607.
2. Особенности ряда математических задач Древней Руси и возможные способы их решения в современной практике решения задач.
В большинстве русских математических рукописей и печатных книг старого времени встречаются занимательные задачи. Много таких задач можно найти в “Арифметике” Л. Ф. Магницкого.
Каждая задача облекается автором в интересную, а чаще практическую форму. Одной из самых ярких характеристик задач «Арифметики» является прикладной характер. Самым главным потребителем арифметических знаний являлось купечество, поэтому практически вся третья часть задач была посвящена тройному правилу и представляла из себя решение задач торговли.
Вспомним о том, что славяне без малого тысячу лет назад уже отлично владели четырьмя действиями арифметики, свободно обращались с довольно большими целыми числами и с маленькими дробями. Думаю, что именно поэтому, все задачи решались путем логических рассуждений. Рассмотрим задачу о цене кафтана, которую не всякий школьник быстро решит.
Задача № 1. “Некий человек нанял работника на год, обещав ему дать 12 рублев и кафтан. Но тот, проработав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном. Он же (хозяин) дал ему по достоинству расчет 5 рублев и кафтан, и знать надлежит, какой цены оный кафтан был”.
I способ. Можно вычислить по действиям, рассуждая логически.
Работник не получил 12 – 5 = 7 (руб.) за 12 – 7 = 5 (месяцев),
поэтому за один месяц ему должны были платить 7:5 = 1,4 (руб.), а за 7 месяцев он должен получил 7 ·1,4 = 9,8 (руб.), так как деньгами он получил 5 рублей, значит кафтан стоил 9,8 – 5 = 4,8 (руб.).
II способ. Решаем, используя пропорции.
Пусть x руб. — стоимость кафтана, (х+12) он должен получить за год, а
(х+12) :12 в месяц. Получил же он (х+5), а в месяц (х+5):7
Получим уравнение, применяя основное свойство пропорции
Решим уравнение Х = 4,8 . Ответ: 4,8 руб. стоит кафтан.
3. «Правило ложного положения»
Одним из способов решения задач часто использовался способ, который основан на предположении. Этим способом сейчас не пользуются или пользуются очень редко. Рассмотрим его на примере двух задач, которые сейчас используют в «Занимательной математике»
Старинные русские задачи из книги Л.Ф.Магницкого «Арифметика»
Задача 1. Летела стая гусей, а навстречу им ещё гусь. Гусь говорит: «Здравствуйте, сто гусей». А ему отвечают: «Нас не сто гусей, а меньше. Если бы нас было столько, да ещё столько, да ещё полстолька, да ещё четверть столька, да ты, гусь вот тогда нас было бы сто гусей». Египетский математик Ахмес, решая эту задачу, сказал бы: «Считай с четырёх». Это значило: «Предположи, что в стае было 4 гуся». Тогда по условию задачи получим:
4 + 4 + 2 + 1 = 11 (гусей).
А так как нужно получить не 11, а 99 гусей (100 – 1 = 99; 99 : 11 = 9),то надо взятое вначале число 4 умножить на 9. Получится правильный ответ 36 гусей.
Поскольку вначале делается неправильное предположение, что число гусей равно 4, этот способ называют теперь «Правилом ложного положения» или «фальшивым правилом».
Рассмотрим перевод задачи с родного языка на алгебраический
Источник