Математические способы решения расчетных задач по химии
Разделы: Химия
Решение расчетных задач – важнейшая составная часть школьного предмета «химия», так как это один из приёмов обучения, посредством которого обеспечивается более глубокое и полное усвоение учебного материала по химии и вырабатывается умение самостоятельного применения полученных знаний.
Чтобы научиться химии, систематическое изучение известных истин химической науки должно сочетаться с самостоятельным поиском решения сначала малых, а затем и больших проблем. Как бы ни были интересны теоретические разделы учебника и качественные опыты практикума, они недостаточны без численного подтверждения выводов теории и результатов эксперимента: ведь химия – количественная наука. Включение задач в учебный процесс позволяет реализовать следующие дидактические принципы обучения: 1) обеспечение самостоятельности и активности учащихся; 2) достижение прочности знаний и умений; 3) осуществление связи обучения с жизнью; 4) реализация предпрофильного и профильного политехнического обучения.
Решение задач является одним из звеньев в прочном усвоении учебного материала, так как формирование теорий и законов, запоминание правил и формул, составление уравнений реакций происходит в действии.
В решении химических задач целесообразно использовать алгебраические приёмы. В этом случае исследование и анализ ряда задач сводятся к преобразованиям формул и подставлению известных величин в конечную формулу или алгебраическое уравнение. Задачи по химии похожи на задачи по математике, и некоторые количественные задачи по химии (особенно на «смеси») удобнее решать через систему уравнений с двумя неизвестными.
Рассмотрим несколько таких задач.
Смесь карбонатов калия и натрия массой 7 г обработали серной кислотой, взятой в избытке. При этом выделившийся газ занял объем 1,344 л (н.у.). Определить массовые доли карбонатов в исходной смеси.
Составляем уравнений реакций:
yл
Обозначим через хг массу карбоната натрия в смеси, а массу карбоната калия – через (7-х)г. Объём газа, выделившегося при взаимодействии карбоната натрия с кислотой, обозначаем через у л, а объём газа, выделившегося при взаимодействии карбоната калия с кислотой, обозначаем через (1,344-у)л.
Над уравнениями реакций записываем введенные обозначения, под уравнениями реакций записываем данные, полученные по уравнениям реакций, и составляем систему уравнений с двумя неизвестными:
Из первого уравнения выражаем у через х:
Решаем уравнение (4) относительно х.
Следовательно, масса карбоната натрия равна 4,24 г.
Массу карбоната калия находим вычитанием из общей массы смеси карбонатов массы карбоната натрия:
Массовые доли карбонатов находим по формуле:
Ответ: массовая доля карбоната натрия равна 60,57%, массовая доля карбоната калия равна 39,43%.
Смесь карбонатов калия и натрия массой 10 г растворили в воде и добавили избыток соляной кислоты. Выделившийся газ пропустили через трубку с пероксидом натрия. Образовавшегося кислорода хватило, чтобы сжечь 1,9 л водорода (н.у.). Напишите уравнения реакций и рассчитайте состав смеси.
Составляем уравнения реакций:
| х г | y л |
| Na2CO3 + 2HCl = 2NaCl + H2O + СО2 (1) | |
| 1моль | 1моль |
| 106г | 22,4л |
| (10-x)г | (1.9-y)л |
| K2CO3 + 2HCl = 2KCl + H2O + CO2^ (2) | |
| 1моль | 1моль |
| 138г | 22,4л |
| х л | 0,95л |
| 2Na2O2 + 2CO2 = 2Na2CO3 + O2 (3) | |
| 2моль | 1моль |
| 44,8л | 22,4л |
| 1,9л | хл |
| 2Н2 + О2 = 2Н2О (4) | |
| 2моль | 1 моль |
| 44,8л | 22,4л |
Обозначим через х г массу карбоната натрия, а масса карбоната калия будет равна (10-х)г.
По уравнению (4) рассчитаем объем кислорода, образовавшегося в процессе реакции (3).
Для этого через х в уравнении обозначим объём кислорода и, исходя из объёма водорода, составим пропорцию и решим её относительно х:
х=0,95л (объём выделившегося кислорода).
Исходя из уравнения (3), рассчитаем объём углекислого газа, образовавшегося при обработке смеси карбонатов натрия и калия избытком соляной кислоты. Для этого составим пропорцию:
Через у л обозначим объём газа, выделившегося в процессе реакции (1), а через (1,9-у)л – объём газа, выделившегося в процессе реакции (2). Составим систему уравнений с двумя неизвестными:
Из уравнения (5) выражаем у через х и подставляем в уравнение (6):
Уравнение (7) решаем относительно х:
х=5,65г (масса карбоната натрия).
Масса карбоната калия находится как разность между массой смеси карбонатов натрия и калия и массой карбоната натрия:
10-5,65=4,35г (масса карбоната калия).
Ответ: массовая доля карбоната натрия равна 56,5%, массовая доля карбоната калия равна 43,5%.
Задачи для самостоятельного решения.
Смесь железа и цинка массой 12,1 г обработали избытком раствора серной кислоты. Для сжигания полученного водорода необходимо 2,24л кислорода (давление 135,6 кПа, температура – 364К). Найдите массовую долю железа в смеси.
Смесь метиловых эфиров уксусной кислоты и пропионовой кислоты массой 47,2г обработали 83,4мл раствора гидроксида натрия с массовой долей 40% (плотность 1,2г/мл). Определите массовые доли эфиров ( в %) в смеси, если известно, что гидроксид натрия, оставшийся после гидролиза эфиров, может поглотить максимально 8,96л оксида углерода (IV).
Эти задачи можно решать и другими способами, но этот способ решения задач по химии способствует развитию логического мышления, даёт возможность показать взаимосвязь математики и химии, формирует умение составлять и применять алгоритмы последовательности действий при решении, дисциплинирует и направляет деятельность на правильное использование физических величин и корректное проведение математических расчётов.
Источник
—> Методика обучения химии —>
В методике обучения химии разработаны различные способы решения расчетных задач. Среди них выделяют следующие:
· физический способ (решение задач с использованием формул математической зависимости);
· решение задач с использованием пропорций;
· метод «приведения к единице»;
· алгебраический способ (решение задач путем составления и решения алгебраических уравнений и неравенств);
3.1. Физический способ
При выборе данного способа решения расчетных задач по химии следует опираться на знания школьников полученные при изучении физики и математики. На уроках физики учащиеся решают задачи с использованием формул математической зависимости величин. При этом они подбирают нужные формулы, решают сначала задачи в общем виде, а затем подставляют числовые значения [3]. В этот блок входят многочисленные типы задач, требующие при решении применения известных формул:
1. 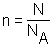
2. 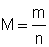
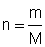
3. 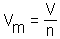
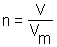
4. 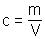
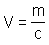
5. 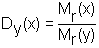
6. w (в-ва)= 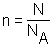
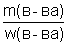
7. c (р.в.)= 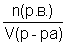
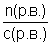
8. φ(газа В)= 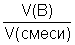
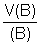
Решение химических задач физическим способом включает следующие этапы: а) подбор формулы для искомой величины; б) преобразование формулы в общем виде; в) подстановка в формулу числовых значений и нахождение ответа.
Пример 1. Какую массу имеет аммиак, занимающий объем 5,6 дм 3 (при н.у.)?
1. Подбираем формулу для нахождения массы m = n • M . В ней неизвестно химическое количество вещества.
2. Подбираем формулу для нахождения химического количеств газа, исходя из условия задачи: n = 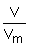
3. Определяем общую искомую формулу для нахождения массы газа: m = 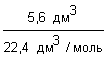
4. Подставляем общую формулу числовые значения и находим массу аммиака.
М r ( NH 3 ) = Ar ( N ) + 3 Ar ( H ) = 14 + 3 · 1 = 17; М( NH 3 ) = 17 г/моль.
m ( NH 3 ) = 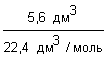
Ответ : аммиак объемом 5,6 дм 3 (при н.у.) имеет массу 4.25 г.
3.2. Решение задач с использованием пропорций
Составление пропорций при решении расчетных задач по химии наиболее часто используется в школьной практике. Этот способ многие учителя считают наиболее понятным учащимся. Однако применение его ограничено, поскольку составление пропорций при решении отдельных типов задач не всегда оправдано. Наиболее рационально применять пропорции при проведении расчетов по химическим уравнениям.
Решение расчетных задач по химии с использованием пропорций включает этапы: а) установление пропорциональной зависимости; б) составление пропорции; в) решение пропорции и нахождение ответа [3].
Пример 2. Какую массу фосфора нужно сжечь для получения оксида фосфора( V ) массой 7,1 г?
1. Составляем уравнение реакции и устанавливаем стехиометрические отношения между известной и искомой величиной:
n 4 моль 2 моль
M 31 г/моль 142 г/моль
2. Составляем пропорцию, рассуждая: при сжигании фосфора массой 124 г образуется оксид фосфора( V ) массой 284 г, а при сжигании фосфора массой x г получается оксид фосфора( V ) массой 7,1 г:
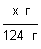
3. Решаем пропорцию: х = 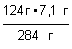
Ответ : для получения оксида фосфора( V ) массой 7,1 г необходимо сжечь фосфор массой 3,1 г.
3.3. Решение задач методом «приведения к единице»
Метод «приведения к единице» при решении расчетных задач по химии близок к предыдущему способу. Он основан на логических рассуждениях, поэтому может быть рекомендован для учащихся старших классов (особенно физико-математического направления).
Рассмотрим решение предыдущей задачи (пример 2) этим способом.
Ход рассуждений: оксид фосфора( V ) массой 142 г содержит химическое количество вещества 1 моль. Следовательно, оксид фосфора( V ) массой 1 г содержит химическое количество вещества 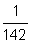
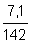
Согласно уравнению реакции при получении оксида фосфора( V ) химическим количеством 4 моль сгорает фосфор химическим количеством 2 моль, а при образовании 0,05 моль оксида фосфора( V ) сгорает 0,1 моль фосфора.
1 моль фосфора имеет массу 31 г, а 0,1 моль фосфора – в 0,1 раза больше, т.е. 31 г · 0,1 = 3,1 г
3.4. Способ подбора
Способом подбора, как правило, решаются химические задачи на расчеты , связанные с нахождением неизвестного элемента или вещества. Рассмотрим этот способ на конкретном примере.
Пример 3. Металл, массой 16 г, взаимодействуя с молекулярным кислородом объемом 4,48 дм 3 (н.у.), образует оксид. Определите, какой это металл.
1. Составляем уравнение реакции получения оксида, приняв за х валентность металла в оксиде.
2. Находим химическое количество прореагировавшего кислорода:
n ( O 2 ) = 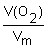
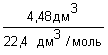
3. Определяем по уравнению реакции химическое количество прореагировавшего металла:
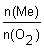
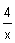
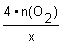
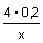
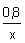
4. Находим молярную массу металла и подбором определяем, какой это металл:
М(Ме) = 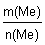
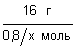
Далее задача решается способом подбора:
если х = I , то М(Ме) = 20 г/моль, такого металла нет;
если х = II , то М(Ме) = 40 г/моль, этот металл – кальций;
если х = III , то М(Ме) = 80, такого металла нет.
Источник