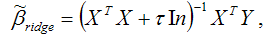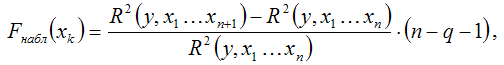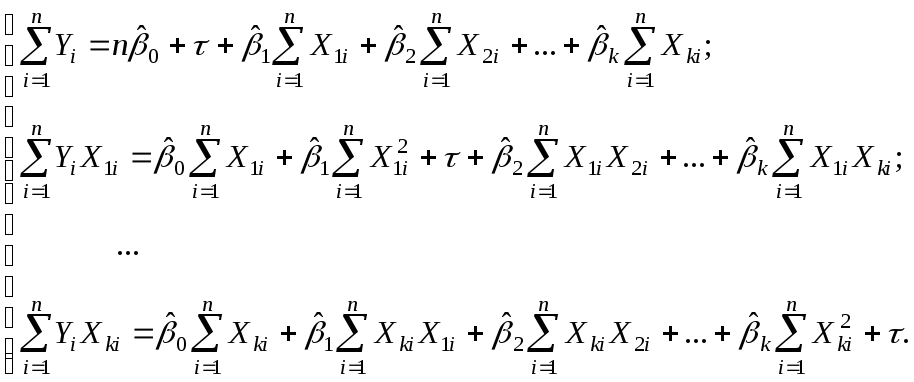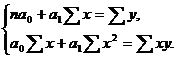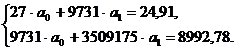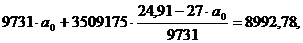Способы решения проблемы мультиколлинеарности

38. Методы устранения мультиколлинеарности

38. Методы устранения мультиколлинеарности

Если оцененную модель регрессии предполагается использовать для изучения экономических связей, то устранение мультиколлинеарных факторов является обязательным, потому что их наличие в модели может привести к неправильным знакам коэффициентов регрессии.

При построении прогноза на основе модели регрессии с мультиколлинеарными факторами необходимо оценивать ситуацию по величине ошибки прогноза. Если её величина является удовлетворительной, то модель можно использовать, несмотря на мультиколлинеарность. Если же величина ошибки прогноза большая, то устранение мультиколлинеарных факторов из модели регрессии является одним из методов повышения точности прогноза.

К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся:

1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна;

2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:

Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов;

Если рассмотренные способы не помогли устранить мультиколлинеарность факторов, то переходят к использованию смещённых методов оценки неизвестных параметров модели регрессии, или методов исключения переменных из модели множественной регрессии.

Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж (ridge).

При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число ?: 10-6 ‹ ? ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:

где ln – единичная матрица.

Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу.

Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.

Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F. При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных xi (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.

Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.

Метод пошагового включения осуществляется по следующему алгоритму:

1) из всех факторных переменных в модель регрессии включаются те переменные, которым соответствует наибольший модуль линейного коэффициента парной корреляции с результативной переменной;

2) при добавлении в модель регрессии новых факторных переменных проверяется их значимость с помощью F-критерия Фишера. При том выдвигается основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии. Обратная гипотеза состоит в утверждении о целесообразности включения факторной переменной xk в модель множественной регрессии. Критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. Наблюдаемое значение F-критерия рассчитывается по формуле:

где q – число уже включённых в модель регрессии факторных переменных.

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии отвергается. Следовательно, включение данной переменной в модель множественной регрессии является обоснованным.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл?Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии принимается. Следовательно, данную факторную переменную можно не включать в модель без ущерба для её качества

3) проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие Fнабл›Fкрит.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

ПЕРЕЧЕНЬ НЕИСПРАВНОСТЕЙ ВИНТОВКИ, ИХ ПОСЛЕДСТВИЯ И СПОСОБ УСТРАНЕНИЯ

ПЕРЕЧЕНЬ НЕИСПРАВНОСТЕЙ ВИНТОВКИ, ИХ ПОСЛЕДСТВИЯ И СПОСОБ УСТРАНЕНИЯ 1. Овальная односторонняя растертость канала ствола с дульной части. В этом случае рассеивание увеличивается, и наблюдается при стрельбах систематическое отклонение пуль в сторону растертости.

§ 229. Основные логические ошибки и способы их устранения

§ 229. Основные логические ошибки и способы их устранения Недостаточное знание законов формальной логики, отсутствие должного логико-смыслового анализа текста ведут к появлению логических ошибок: нарушение причинно-следственных отношений, сопоставление несопоставимых

Упражнения для устранения психической напряженности и нервного раздражения

Упражнения для устранения психической напряженности и нервного раздражения Восточная медицина объясняет, что психической деятельностью управляет не голова, а внутренние органы: энергия — в легких, ум — в сердце, дух — в печени, воля — в селезенке, стремления — в

Для устранения привычных запоров

Для устранения привычных запоров Кое-какие сведения о причине запора необходимы, поскольку правильный процесс выведения отработанных пищевых масс является важным фактором здоровья. Каловые массы застаиваются в сигмовидной кишке, которая расположена вниз и слева от

Глава 4. ЦЕНТРАЛЬНОЕ ОТОПЛЕНИЕ: РАБОТА, НЕИСПРАВНОСТИ И СПОСОБЫ ИХ УСТРАНЕНИЯ

Глава 4. ЦЕНТРАЛЬНОЕ ОТОПЛЕНИЕ: РАБОТА, НЕИСПРАВНОСТИ И СПОСОБЫ ИХ УСТРАНЕНИЯ Неисправности системы и их устранение Система отопления должна обеспечивать расчетную (требуемую по нормам) температуру воздуха в квартире. Расчетная температура воздуха в квартире должна

ГЛАВА V ПРИЧИНЫ НЕИСПРАВНОСТЕЙ И ОТКАЗОВ В РАБОТЕ АВТОМАТИЧЕСКОГО КАРАБИНА И СПОСОБЫ ИХ УСТРАНЕНИЯ

ГЛАВА V ПРИЧИНЫ НЕИСПРАВНОСТЕЙ И ОТКАЗОВ В РАБОТЕ АВТОМАТИЧЕСКОГО КАРАБИНА И СПОСОБЫ ИХ УСТРАНЕНИЯ Автоматический карабин, как и всякое автоматическое оружие, нуждается во внимательном уходе, сбережении и умелом обращении. При соблюдении этих условий является

37. Определение мультиколлинеарности. Последствия мультиколлинеарности. Методы обнаружения мультиколлинеарности

37. Определение мультиколлинеарности. Последствия мультиколлинеарности. Методы обнаружения мультиколлинеарности Наибольшие затруднения в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторных переменных, когда более

Возможные неполадки и способы их устранения

Возможные неполадки и способы их устранения ASIO4ALL представляет себя приложениям как автономный драйвер, но в некоторых конфигурациях фактически таким не является. Поэтому некоторые проблемы могут возникать не по его вине, даже если внешне это выглядит иначе. Особо можно

Задержки при стрельбе из пистолета и способы их устранения

Задержки при стрельбе из пистолета и способы их устранения Пистолет при правильном обращении с ним, внимательном уходе и сбережении, своевременном ремонте и т. п. является надежным и безотказным оружием. Однако, при длительной работе вследствие износа частей и

ГЛАВА СЕДЬМАЯ Причины задержек и способы их устранения

ГЛАВА СЕДЬМАЯ Причины задержек и способы их устранения Перечень задержек Причины появления Способ устранения § 70. Недоходы?незакрывание затвора а) Сильное загрязнение механизма, в особенности патронника ствола Разобрать, прочистить все части, обратив особое

17. Способы устранения дефектов штукатурки

17. Способы устранения дефектов штукатурки Со временем по разным причинам в штукатурке неизбежно появляются трещины, выбоины, царапины. Ремонтнику, приглашенному устранить повреждения, нужно прежде всего установить и устранить причину, вызвавшую это явление.Наиболее

Источник

3.6 Мультиколлинеарность и методы ее устранения

Одним из важнейших этапов построения регрессии является отбор факторов 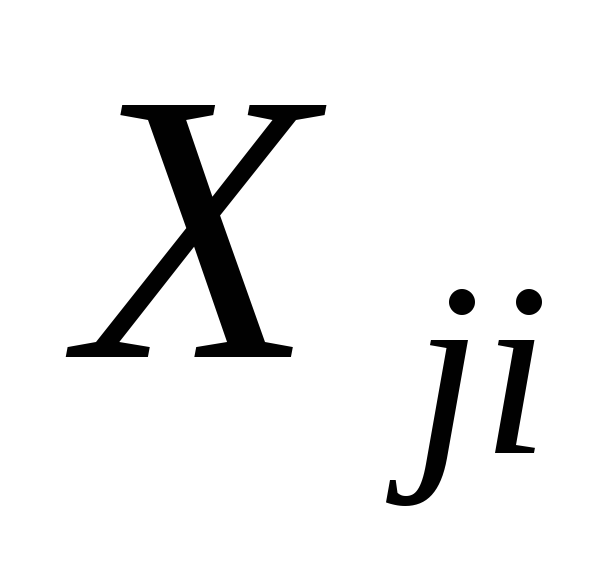,j=1. k, i=1,2,…,n, включаемых в регрессию (3.1). Наибольшее распространение получили следующие методы построения уравнения множественной регрессии: метод исключения, метод включения, шаговый регрессионный анализ. Перечисленные методы дают близкие результаты: отсев факторов из полного их набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый метод).

Наиболее широко используются для решения вопроса об отборе факторов частные коэффициенты корреляции, оценивающие в чистом виде тесноту связи между фактором и результатом.

При включении факторов следует придерживаться правила, согласно которому число включаемых в модель объясняющих переменных должно быть в 5-6 раз меньше объема совокупности, по которой строится регрессия. Иначе число степеней свободы остаточной вариации будет мало, и параметры уравнения регрессии окажутся статистически незначимы.

Иногда при отборе переменных-факторов нарушается предположение (3.5). В этом случае говорят, что объясняющие переменные 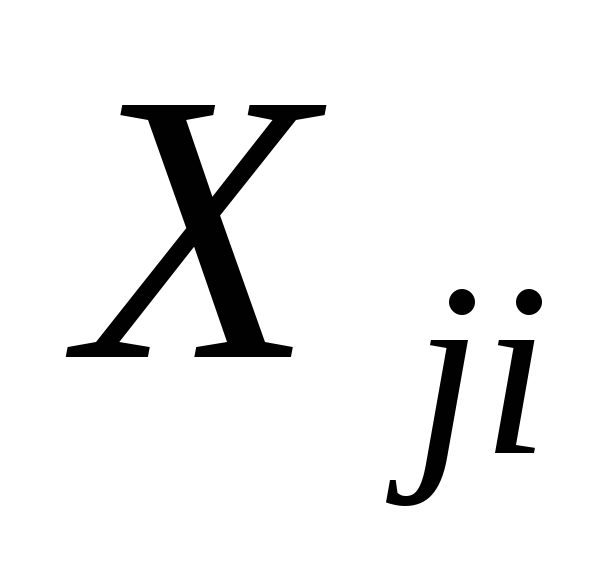,j=1. k,i=1,2,…,n модели характеризуются свойством полной (строгой)мультиколлинеарности. В этом случае система (3.6) не может быть разрешена относительно неизвестных оценок коэффициентов. Строгая мультиколлинеарность встречается редко, так как ее несложно избежать на предварительной стадии отбора объясняющих переменных.

Реальная (частичная) мультиколлинеарность возникает в случаях достаточно сильных линейных статистических связей между переменными 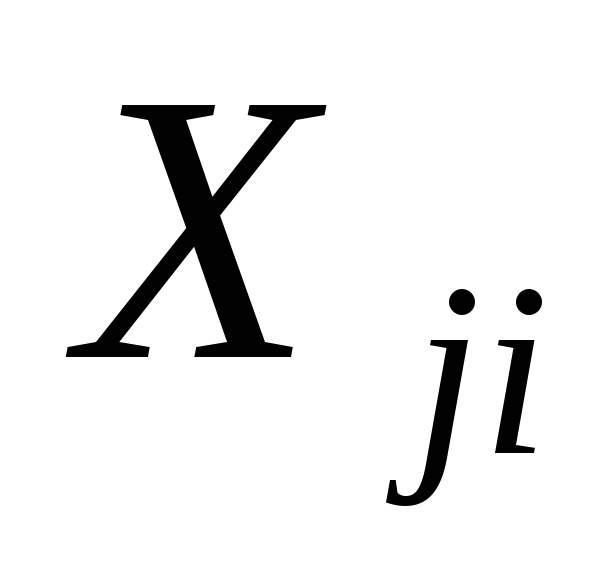,j=1. k,i=1,2,…,n. Точных количественных критериев для проверки наличия мультиколлинеарности не существует, но имеются некоторые практические рекомендации по выявлению мультиколлинеарности.

1. Если среди парных коэффициентов корреляции между объясняющими переменными имеются значения 0,75-0,80 и выше, это свидетельствует о присутствии мультиколлинеарности.

Пример. В примере 2 между переменными K и L коэффициент корреляции равен 0,96, а между lnK и lnL чуть меньше 0,89. 

2. О присутствии явления мультиколлинеарности сигнализируют некоторые внешние признаки построенной модели, являющиеся его следствиями:

— некоторые из оценок 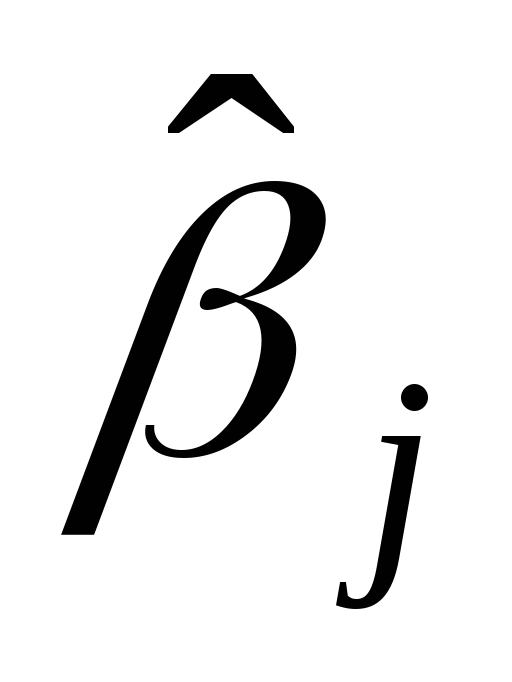,j=1,2,…,k имеют неправильные с точки зрения экономической теории знаки или неоправданно большие по абсолютной величине значения,

— небольшое изменение исходной выборки (добавление или изъятие малой порции данных) приводит к существенному изменению оценок коэффициентов модели вплоть до изменения их знаков,

— большинство оценок коэффициентов регрессии оказываются статистически незначимо отличающимися от нуля, в то время как в действительности многие из них имеют отличные от нуля значения, а модель в целом является значимой при проверке с помощью F-критерия.

Методы устранения мультиколлинеарности.

1. Проще всего удалить из модели один или несколько факторов.

2. Другой путь состоит в преобразовании факторов, при котором уменьшается корреляция между ними. Например, при построении регрессий на основе временных рядов помогает переход от первоначальных данных к первым разностям =Y_t—Y_t-1. В примере 2 переход от переменных K и L к их логарифмам уменьшил коэффициент корреляции с 0,96 до 0,89.

3. Использование в уравнении регрессии взаимодействия факторов, например, в виде их произведения.

4. Использование так называемой ридж-регрессии (гребневой регрессии). В этом случае к диагональным элементам системы (3.6) добавляется «гребень»  (небольшое число, как правило, от 0,1 до 0,4):

Это делает получаемые оценки смещенными, но уменьшает средние квадраты ошибок коэффициентов.

5. Использование метода главных компонент 6 .

6. Отбор наиболее существенных объясняющих переменных на основе методов исключения, включения, шаговой регрессии, которые используют для принятия решения F-критерий.

Источник

Понятие мультиколлинеарности. Методы устранения мультиколлинеарности.

Вариант № 2

ТЕОРЕТИЧЕСКОЕ ЗАДАНИЕ

Понятие мультиколлинеарности. Методы устранения мультиколлинеарности.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной (явной) и стохастической (скрытой) формах.

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица 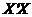особенная, т. к. содержит линейно зависимые векторы – столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа.

В экономических исследованиях мультиколлинеарность чаще проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица 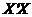в этом случае является неособенной, но ее определитель очень мал.

Точных количественных критериев для определения наличия или отсутствия мультиколлинеарности не существует. Тем не менее некоторые эвристические подходы по ее выявлению.

Один из таких подходов заключается в анализе корреляционной матрицы между объясняющими переменными 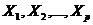и выявлении пар переменных, имеющий высокие коэффициенты корреляции (обычно больше 0,8). Если такие переменные существуют, то говорят о мультиколлинеарности между ними.

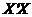
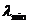
Другой подход состоит в исследовании матрица . Если определитель матрицы либо ее минимальное собственное значение близки к нулю, то говорят о мультиколлинеарности.

Обычно выделяются следующие последствия мультиколлинеарности:

1. Большие дисперсии (стандартные ошибки) оценок. Это затрудняет нахождение истинных значений определяемых величин и расширяет интервальные оценки, ухудшая их точность.

2. Уменьшаются t – статистики коэффициентов, что может привести к неоправданному выводу о существенности объясняющей переменной на зависимую переменную.

3. Оценки коэффициентов по МНК и их стандартные ошибки становятся очень чувствительными к изменениям данных, т. е. становятся неустойчивыми.

4. Затрудняется определение вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.

5. Возможно получение неверного знака у коэффициента регрессии.

Точных количественных критериев для определения наличия (отсутствия) мультиколлинеарности не существует. Тем не менее существуют некоторые рекомендации по выявлению мольтиколлинеарности.

1. В первую очередь анализируют матрицу парных коэффициентов корреляции

,

точнее ту ее часть, которая относится к объясняющим переменным:

.

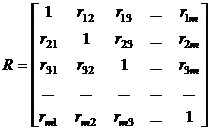
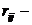
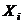
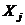
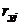
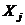
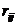
Здесь парный коэффициент корреляции между переменными , ; — парный коэффициент корреляции между Y и . Считается, что наличие коэффициентов превышающих по абсолютной величине 0,75 – 0,8, свидетельствует о наличии мультиколлинеарности.

2. Если определитель матрицы 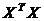близко к нулю (например, одного порядка с накапливающимися ошибками вычислений), то это свидетельствует о наличии мультиколлинеарности.

3. Коэффициент детерминации 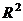достаточно высок, но некоторые из коэффициентов регрессии статистически значимы, т. е. они имеют низкие t – статистики.

4. Высокие частные коэффициенты корреляции свидетельствует о наличии мультиколлинеарности. При изучении многомерных связей необходимо измерять действительную силу линейной связи между двумя переменными, очищенную от влияния на рассматриваемую пару переменных других факторов.

Для устранения или уменьшения мультиколлинеарности используется ряд методов. Самый простой из них состоит в том, что из двух объясняющих переменных, имеющих высокий коэффициент корреляции (больше 0,8), одну переменную исключают из рассмотрения. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании экономических соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из переменных, которая имеет больший коэффициент корреляции с зависимой переменной.

Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещенных оценок, определенных по методу наименьших квадратов, к смещенным оценкам, обладающих меньшим рассеянием относительно оцениваемого параметра.

Отметим, что в ряде случаев мультиколлинеарность не является таким уж «злом», чтобы прилагать существенные усилия по ее выявлению и устранению. В основном все зависит от целей исследования.

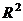
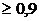
Если основная задача модели – прогноз будущих значений зависимой переменной, то при достаточно большом коэффициенте детерминации ( ) наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели (если в будущем коррелированными переменными будут те же отношения, что и ранее).

Если необходимо определить степень влияния каждой из объясняющих переменных на зависимую переменную, то мультиколлинеарность, приводящая к увеличению стандартных ошибок, скорее всего, исказит истинные зависимости между переменными. В этой ситуации мультиколлинеарность является серьезной проблемой.

Единого метода устранения мультиколлинеарности, годного в любом случае, не существует. Это связано с тем, что причины и последствия мультиколлинеарности неоднозначны и во многом зависят от результатов выборки.

Исключение переменной(ых) из модели

Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных. При применении данного метода необходима определенная осмотрительность. В данной ситуации возможны ошибки спецификации, поэтому в прикладных эконометрических моделях желательно не исключать объясняющие переменные до тех пор, пока Мультиколлинеарность не станет серьезной проблемой.

Получение дополнительных данных или новой выборки

Поскольку мультиколлинеарность напрямую зависит от выборки, то, возможно, при другой выборке мультиколлинеарности не будет либо она не будет столь серьезной. Иногда для уменьшения мультиколлинеарности достаточно увеличить объем выборки. Например, при использовании ежегодных данных можно перейти к поквартальным данным. Увеличение количества данных сокращает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость. Однако получение новой выборки или расширение старой не всегда возможно или связано серьезными издержками. Кроме того, такой подход может усилить автокорреляцию. Эти проблемы ограничивают возможность использования данного метода.

Изменение спецификации модели

В ряде случаев проблема мультиколлинеарности модели может быть решена путем изменения спецификации модели, либо добавляются объясняющие переменные, не учтенные в первоначальной модели, но существенно влияющие на зависимую переменную. Если данный метод имеет основания, то его использование уменьшает сумму квадратов отклонений, тем самым сокращая ошибку регрессии. Это приводит к уменьшению стандартных ошибок коэффициентов.

Использование предварительной информации о некоторых параметрах

Иногда при построении модели множественной регрессии можно воспользоваться предварительной информацией, в частности известными значениями некоторых коэффициентов регрессии. Вполне вероятно, что значения коэффициентов, рассчитанные для каких – либо предварительных (обычно более простых) моделей либо для аналогичной модели по ранее полученной выборке, могут быть использованы для разрабатываемой в данный момент модели.

При обосновании выбора той или иной модели исследователь сталкивается с рядом трудностей, которые можно разделить на несколько групп. Первая группа трудностей вызвана мультиколлинеарностью переменных, которая существенно проявляется при решении системы (6). Мультиколлинеарность переменных означает, что среди объясняющих переменных имеются явно линейно зависимые (коэффициенты парной корреляции близки к единице). Тогда определитель матрицы системы (6) может быть равен или близок к нулю. Отсюда следует, что оценки b * коэффициентов множественной линейной регрессии находятся неустойчиво, имеют большие стандартные ошибки. Это не позволяет сделать достоверных выводов о модели в целом. Простейший способ устранения мультиколлинеарности переменных состоит в отбрасывании одной или нескольких переменных, вызывающих мультиколлинеарность.

Вторая группа трудностей вызвана автокорреляцией остатков. Наличие автокорреляции остатков не позволяет применять МНК в указанной выше форме, иначе говоря, полученными оценками коэффициентов b * пользоваться нельзя. Способ устранения автокорреляции состоит в оценке коэффициентов корреляции между переменными и их явный учет в формулах МНК.

Третья группа трудностей обусловлена наличием гетероскедастичности наблюдений. Она связана с тем, что дисперсия погрешности e_i каждого наблюдения не одинакова и равна D_i. Для устранения этой трудности необходимо оценить D_i и учесть ее в формуле для функции L(b), а именно вычислять L(b), используя соотношение

Одной из причин гетероскедастичности наблюдений является замена переменных в нелинейных моделях. В обоих случаях необходимо изучать выборку остатков.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

Построить зависимость по двум признакам. Оценить полученные результаты. Объяснить экономический смысл полученных результатов.

Объем производства	Фондоотдача	Объем производства	Фондоотдача
348	0,82	359	0,93
349	0,82	360	0,94
350	0,83	361	0,96
351	0,84	362	0,95
352	0,85	361	0,95
352	0,86	366	0,97
353	0,86	369	0,97
354	0,87	370	0,99
355	0,88	372	0,98
356	0,89	372	1,01
358	0,90	376	1,02
359	0,91	374	1,03
357	0,91	379	1,05
356	0,92

Для построения зависимости воспользуемся методом наименьших квадратов. Уравнение регрессии будем искать в виде линейного уравнения .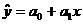

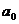
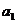
Для оценки параметров и уравнения линейной регрессии по методу наименьших квадратов используем систему нормальных уравнений:

Вычислим все необходимые суммы на основании расчетной таблицы:

№ п/п	Объем производства x	Фондоотдача y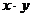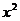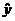
1	348	0,82	285,36	121104	0,8891
2	349	0,82	286,18	121801	0,9143
3	350	0,83	290,50	122500	0,929
4	351	0,84	294,84	123201	0,9311
5	352	0,85	299,20	123904	0,9332
6	352	0,86	302,72	123904	0,9437
7	353	0,86	303,58	124609	0,9584
8	354	0,87	307,98	125316	0,9626
9	355	0,88	312,40	126025	0,9815
10	356	0,89	316,84	126736	0,9899
11	358	0,90	322,20	128164	0,9941
12	359	0,91	326,69	128881	1,0109
13	357	0,91	324,87	127449	1,0151
14	356	0,92	327,52	126736	1,0235
15	359	0,93	333,87	128881	1,0319
16	360	0,94	338,40	129600	1,0193
17	361	0,96	346,56	130321	1,0361
18	362	0,95	343,9	131044	0,9731
19	361	0,95	342,95	130321	0,9521
20	366	0,97	355,02	133956	1,0151
21	369	0,97	357,93	136161	1,0487
22	370	0,99	366,30	136900	1,0529
23	372	0,98	364,56	138384	1,0571
24	372	1,01	375,72	138384	1,0613
25	376	1,02	383,52	141376	1,0739
26	374	1,03	385,22	139876	1,0781
27	379	1,05	397,95	143641	1,0844
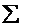	9731	24,91	8992,78	3509175

Система нормальных уравнений будет иметь вид:

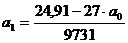
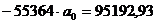
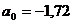
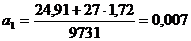
Из первого уравнения выразим: , подставим во второе

, , .

Из полученного уравнения регрессии 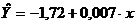следует, что при увеличении объема производства Х на 1 ед. фондоотдача Y увеличится в среднем на 0,007 ед.

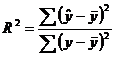
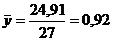
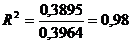
Для оценки параметров полученных результатов вычислим коэффициент детерминации по формуле: . Имеем .

. Это обозначает, что вариация зависимой переменной y – фондоотдачи на 98% объясняется изменчивостью объясняющей переменной х – объемом производства.

Значение коэффициента парной корреляции 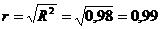значительно приближено к 1 , значит связь между переменными х и y достаточно тесная.

Список использованной литературы

1. Кремер Н. Ш., Путко Б. А. Эконометрика: Учебник для вузов / Под ред. Проф. Н. Ш. Кремера. – М.: ЮНИТИ – ДАНА, 2002

2. Эконометрика: Учебник / Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2003

Источник