Способы решения примеров до 100

Методика сложения и вычитания в пределах 100

Методика изучения сложения и вычитания в пределах 100

— уметь пользоваться порядковыми числительными при счёте предметов

— осознать взаимосвязь порядкового номера от смены предмета

Сравнение численностей множеств.

— сравнение равночисленных множеств

— сравнение неравночисленных множеств

— преобразование неравночисленных множеств в равночисленные и наоборот

4) Пространственные и временные представления :

— вверху, внизу и т. п.

Логические игры и упражнения.

Пример: игры с обручами.

Подготовка к введению и знакомству с арифметическими действиями.

Методика изучения нумерации чисел первого десятка.

Нумерация – способы образования, чтения и записи чисел.

Задачи изучения темы «Нумерация чисел 1-го десятка»:

1) Знать последовательность чисел 0-10:

— считать в прямом и обратном порядке

— уметь назвать число

— знать числа, следующие за, предшествующие, между

— знать место числа 0 в ряду чисел

Знать способы образования чисел 0-10.

— на основе практических действий по добавлению или изыманию одного предмета

Уметь сравнивать числа в пределах 10.

— с опорой на сравнение множеств

— на основе места в натуральном ряду

— на основе знания состава чисел

Уметь обозначать каждое число печатной и письменной цифрой.

Методика изучения сложения и вычитания в пределах десяти

1)Сложение и вычитание в пределах 10 на практической основе (конц. «Десяток»)

2)слож/вычит. в пределах 10 на теоретической основе или непосред. табличное слож/вычит (конц. «Двадцаток») Вычисление на теоретической основе-вычисление без опоры на практическую основу.

Этапы изучения табличного слож/вычит.:

Теоретическая основа: (порядок чисел) свойсвто натурального ряда чисел—каждое следующее число на единицу больше предыдущего и наоборот . 2+1=3

Теоретическая основа: приём прибавления/ вычитания по частям или группами

3) слож. 5,6,7,8,9 [ответ до 10]

Теоретическая основа: (коммутативность) переместительное свойство сложения

· использование приема по частям

· (изучение) знакомство с переместительным свойством сложения

Доказать в начальной школе=показать, сделать очевидным, наглядным=> предматематическое доказательство

к к к з з к-красный кружок з-зеленый

2 способ С использование идеи физического перемещения

3 способ С использование идеи классификации

критерии классификации по цвету : 2+3=5 по размеру : 3+2=5

· использование переместительного свойства

Теоретическая основа : (испол.) взаимосвязь между суммой и слагаемыми

· использование знакомого приема по частям

· знакомство со взаимосвязью между суммой и слагаемыми

· использование этой взаимосвязи

Методика изучения нумерации чисел в пределах ста

Знакомство с числами от 21 до 100 начинают с устной нумерации . Образование и называние чисел 30, 40, 50, 60,70, 80, 90, 100 объясняется в процессе счета десятками : 1 десяток- десять единиц, 2 десятка- двадцать единиц….девять десятков- девяносто единиц, десять десятков –сто единиц. При введении и анализе названий десятков обращается внимание на то, что все они, кроме «сорок» и «сто», образованны по одному принципу.

Освоив счет десятками, учащиеся знакомятся с образованием и именами любых чисел в пределах сотни : 2 десятка и 5 единиц- это двадцать пять; 4 десятка и семь единиц- это сорок семь и т.п. Упражнения на образование чисел чередуются с упражнениями на разложение чисел: пятьдесят шесть- это 5 десятков и 6 единиц; девяносто один- это 9 десятков и 1 единица и т.д.

При изучении письменно нумерации учащиеся знакомятся с понятиями разряда и разрядного числа. Поясняется, что, например, тридцать семь- это 3 десятка и 7 единиц, но можно сказать и по-другому: 3 единицы второго разряда и 7 единиц первого разряда. Здесь полезно использовать карточки с разрядными числами , которые помогают усвоить состав числа, представить его в виде суммы разрядных слагаемых (56=50+6). Эти навыки затем используются при изучении операций над натуральными числами.

Изучая нумерацию в пределах 100, учащиеся выполняют упражнения на сложение и вычитание:

1) прибавление и вычитание числа 1;

2 )прибавление к целому числу десятков однозначного числа;

3) вычитание всех десятков из числа;

4 )прибавление целого числа десятков к однозначному числу:

5) вычитание всех единиц из числа.

Методика вычислений здесь та же, что и для подобных случаев в пределах 20 . При выполнении упражнений на присчитывание и отсчитывание единицы, числе, кратных 10, используется наглядное пособие «лента ста» — метровая лента с обозначенными сантиметрами и дециметрами.

Усвоению последовательности чисел первой сотни в натуральном ряду способствуют также следующие упражнения:

1 )назовите число, предшествующее числу 27 (после какого числа при счете называют число 27?);

2 )назовите число, следующее за числом 27 (перед каким числом при счете называют число 28?);

3) между какими числами называют при счете число 27?

Работа по усвоению нумерации продолжается и при изучении операций сложения и вычитания в пределах 100.

Итак, изучив, нумерацию чисел в пределах 100, учащиеся должны усвоить :

1 .имена двузначных чисел в устной и письменной речи, их десятичный состав;

2 .расположение чисел до 100 в натуральном ряду;

3 .смысл терминов: «единица первого разряда», «единица второго разряда», «разрядное число», «однозначное число», «двузначное число».

Методика изучения сложения и вычитания в пределах 100

Нумерация – способы образования, чтения и записи чисел.

Цифра – символ для записи числа.

“ Нумерация чисел в концентре сотня”:

— устные приёмы сложения/вычитания

1) прибавление числа к сумме (сначала складываются единицы) 56+3=56(50+6)+3=50+(6+3)

2) прибавление суммы к числу (сложение по частям) 9+6=9+6(1+5)=(9+1)+5

3) прибавление суммы к сумме (десятки складываются с десятками, а единицы с единицами) 12+15=12(10+2)+15(10+5)=(10+10)+(2+5)=20+7=27

1) вычитание чисел из суммы (сначала вычитаем единицы, потом прибавляем к десяткам) 47-3=47(40+7)-3=40+(7-3)

2) вычитание суммы из числа (вычитаем по частям) 12-5=12-5(2+3)=(12-2)-3

3) вычитание суммы из суммы (вычитаем десятки, вычитаем единицы, полученные разности складываем 25-12=25(20+5)-12(10+2)=(20-10)+(5-2)=10+3=13

— пишем единицы под единицами, десятки под десятками

— складываем единицы, пишем под единицами

— складываем десятки, пишем под десятками

— пишем единицы под единицами, десятки под десятками

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Мудрая Сова: Здравствуйте, дорогие ребята! Вы меня узнали? Конечно, это я, мудрая Сова!

Я рада приветствовать вас снова в нашей лесной школе. Мои верные друзья : черепашка Маша, кошка Алиса и енот Кузьма отлично отдохнули летом и готовы помогать вам изучать математику в третьем классе.

Вы все помните, что мы с вами изучали в прошлом году? Давайте проверим ваши знания.

В прошлом году наши уроки начинались с устного счета. Напомните, для чего он нужен? Правильно, для того, что разогреть наш мозг и подготовиться решать примеры и задачи.

Кузьма уже подготовил вам задания для устного счета.

1. Задание для устного счета

36 увеличьте на 8.

На сколько 18 больше 9?

Уменьшите 17 на 8.

19 меньше неизвестного числа на 12. Чему равно неизвестное число?

Найдите сумму чисел: 16 и 17.

Вычислите значение разности чисел: 24 и 16.

Сумма каких однозначных чисел равна 16?

Для детского сада купили 16 кукол, а мячей на 9 меньше. Сколько мячей купили для детского сада?

Сыну 22 года. Его отцу 50 лет. На сколько лет сын моложе отца?

Ответы в конце урока!

Повторяем состав чисел

Сова: Хорошо. Посмотрим, как ребята помнят состав чисел. Что такое состав чисел? Правильно. Это два числа, из которых состоит каждое число. А зачем нам нужно знать состав чисел? Чтобы быстро считать удобным способом.

Давайте вспомним, как мы это делали во втором классе. Например, нам нужно найти сумму чисел 23 и 50. Что мы с вами будем делать? Разложим число 27 на два слагаемых: 20 и 7. Теперь нам легче будет сложить десятки и к полученной сумме прибавить три единицы.

Вспомнили? Решите несколько примеров, используя свои знания о составе чисел.

Сова: Молодцы, ребята! О, черепашке Маше уже не терпится решать с вами задачи. Что ты ребятам сегодня приготовила?

Решаем задачи различными способами

Черепашка Маша: Мы сегодня с ребятами вспомним, как решать задачи разными способами.

Задание 2. Найдите из предложенных утверждений правильные:

Задачу можно решить по действиям с пояснениями или по вопросам.

Задачу можно решить, используя свой опыт. V

Задачу можно решить выражением.

Задачу можно решить арифметически. V

Задачу можно решить алгебраически . V

Задачу можно решить графически. V

Ответ в конце урока!

Вспомним, что значит решить задачу, используя свой опыт? Помните, в первом классе мы еще не знали сложение и вычитание, но используя палочки или другой счетный материал, мы решали задачи про птиц, которые прилетели или улетели, про морковки и зайцев, пересчитывая их. Это и есть наш опыт.

Познакомившись с понятием сложение и вычитание, мы стали записывать решение уже арифметически, с помощью примеров.

Задачи на умножение и деление мы решали с помощью чертежа или рисовали схему – это графический способ.

А уравнения мы решаем, каким способом? Правильно, алгебраическим, т.к. неизвестное число обозначали латинской буквой и находили его значение.

Вот вам три задачи, которые нужно решить, выбрав один из известных вам способов и указать его в ответе.

Задача 1. Почтальон разнес 47 писем. Ему осталось разнести еще 15. Сколько всего писем оно должен разнести?

47 + 15 = 62 (письма) – арифметический способ.

Задача 2. Красная шапочка сначала шла до автобусной остановки 10 минут, потом ехала на автобусе 39 минут, и затем, до бабушкиного дома её подвез Буратино. Всего в пути Красная шапочка была час. Сколько минут её катал на велосипеде Буратино?

Решили графическим способом.

Задача 3. В школьную библиотеку из второго класса записалось 46 школьников. Девочек, 24 , остальные мальчики. Сколько мальчиков записалось в школьную библиотеку?

Решили алгебраическим способом.

Сова: Ай да ребята! Ай да молодцы! Как ловко вы решаете задачи различными способами. Пришло время немного отдохнуть.

Определяем верные и неверные равенства

Сова : Продолжаем работать. Вспомним, что такое равенство и неравенство?

Равенство это когда левая часть выражения (примера) равна правой. Например, 12+4 = 16. В равенстве используют знак «=»

А неравенство – левая часть выражения больше или меньше правой. Например, 12+4

Повторили? А теперь, закрепим.

Задача 4. Вам нужно будет выписать только неверные неравенства.

(Правильные ответы выделены курсивом)

А кто у нас тут, рисует различные геометрические фигуры? Алиса!

Геометрические фигуры и задачи

Кошка Алиса: Мур, мур! Да, я люблю рисовать различные геометрические фигуры. А ребята помнят геометрические фигуры?

Задача 5. Назовите все геометрические фигуры, которые видите.

Сова: Ну что скажешь, Алиса, знают ребята геометрические фигуры?

Алиса: Мур, мур, знают. А вот, помнят они, как чертить отрезки, делить их и обозначать буквами?

Сова: А ты проверь. Дай им задачу и посмотри, помнят или забыли за лето?

Алиса: Хорошо. Вот вам геометрическая задача.

Задача 6. Начертите в тетради отрезок АВ длиной 1 дм 2 см. Разделите его точками на три равные части. Обозначьте буквами отмеченные точки. Запишите все полученные отрезки.

Ответ в конце урока!

Алиса: Великолепно! Мур, мур. Молодцы, ребята! Пойду придумывать вам новые геометрические задачи.

Логическая задача от мудрой Совы

Сова: Наш урок подходит к концу. Но у меня для вас есть задача на смекалку.

Задача 7. В записи 8 8 8 8 8 8 поставьте между некоторыми цифрами два знака действия и скобки так, чтобы полученное выражение имело значение

Правильный ответ в конце урока!

Ребята, давайте подведем итоги нашего сегодняшнего урока.

Сегодня мы повторили темы:

-решение задач различными способами;

-верные и неверные равенства;

И давайте сверим ответы:

Задание 1. 44, 9,9,31,33,8,8,7,28

Задание 2. (правильные ответы выделены V )

Первое и третье утверждение о формах записи задачи, а не способ их решения.

Задача 6. АС, СD, DB.

Задача 7.

1. (88-88) х 88 = 0 х 88 = 0

2. (888-88):8 = 800 : 8 = 100

Спасибо моим друзьям: Кузьме, Маше и Алисе за помощь в проведении урока.

Источник

Как быстро считать в уме: приемы устного счета больших чисел

• 12 января 2021 г.
• 15 минут
• 279 307
• 9

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

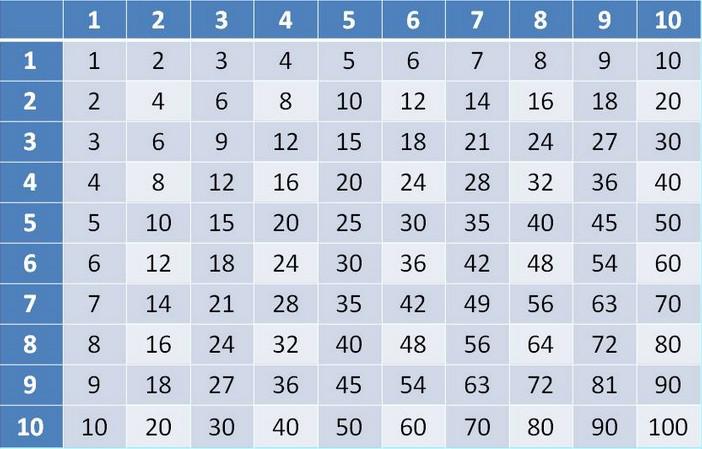
Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник