Видеоурок по математике «Показательные уравнения»
В уроке показаны различные примеры решения показательных уравнений.
Показательное уравнение — это уравнение, в котором неизвестные (иксы) и выражения с ними находятся в показателях каких-то степеней.
Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!
 | Сергей Кравцов рассказал о проекте по обновлению правил русского языка |
 | В Министерстве просвещения разработали меморандум по воспитательной работе в школах |
 | Поздравляем с наступающим Днём учителя! |
 | В Минпросвещения и Рособрнадзоре уже провели работу по снижению количества контрольных работ в школах |
 | Бесплатный вебинар «Дети в Интернете. Все, что нужно знать о контентной фильтрации в образовательных учреждениях» |
Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.
© 2007 — 2021 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте (презентации, конспекты, статьи и пр.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
Администрация сайта готова оказать поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
Источник
Решение показательных уравнений
В этой статье вы познакомитесь со всеми типами показательных уравнений и алгоритмами их решения, научитесь распознавать, к какому типу принадлежит показательное уравнение, которое вам надо решить, и применять для его решения соответствующий метод. Подробное решение примеров показательных уравнений каждого типа вы сможете посмотреть в соответствующих ВИДЕОУРОКАХ.
Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.
Прежде чем начать решать показательное уравнение, полезно сделать несколько предварительных действий , которые могут значительно облегчить ход его решения. Вот эти действия:
1. Разложите все основания степеней на простые множители.
2. Корни представьте в виде степени.
3. Десятичные дроби представьте в виде обыкновенных.
4. Смешанные числа запишите в виде неправильных дробей.
Пользу этих действий вы осознаете в процессе решения уравнений.
Рассмотрим основные типы показательных уравнений и алгоритмы их решения.
1. Уравнение вида
Это уравнение равносильно уравнению 
Посмотрите в этом ВИДЕОУРОКЕ решение уравнения 
этого типа.
2. Уравнение вида
В уравнениях этого типа:
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени равны.
Чтобы решить это уравнение, нужно вынести за скобку множитель в наименьшей степени.
Пример решения уравнения этого типа:
посмотрите в ВИДЕОУРОКЕ.
3. Уравнение вида
Уравнения этого типа отличаются тем, что
а) все степени имеют одинаковые основания
б) коэффициенты при неизвестном в показателе степени разные.
Уравнения такого типа решаются с помощью замены переменных. Прежде чем вводить замену, желательно освободиться от свободных членов в показателе степени. (
, 
, и т.д)
Посмотрите в ВИДЕОУРОКЕ решение уравнения этого типа:
4. Однородные уравнения вида 
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородные уравнения решаются по сходному алгоритму.
Чтобы решить уравнение такого типа, разделим обе части уравнения на 
(можно разделить на 
или на 
)
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
В нашем случае, поскольку выражение не равно нулю ни при каких значениях неизвестного, мы можем делить на него без опаски. Разделим левую часть уравнения на это выражение почленно. Получим:
Сократим числитель и знаменатель второй и третьей дроби:
, причем 
0″ title=»t>0″/> 
при всех допустимых значениях неизвестного.
Получим квадратное уравнение:
Решим квадратное уравнение, найдем значения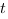 
, которые удовлетворяют условию 0″ title=»t>0″/>, а затем вернемся к исходному неизвестному.
Смотрите в ВИДЕОУРОКЕ подробное решение однородного уравнения:
При решении этого уравнения будем исходить из того, что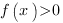 
0″ title=»f(x)>0″/>
Исходное равенство выполняется в двух случаях:
1. Если 
, поскольку 1 в любой степени равна 1,
или
2. При выполнении двух условий:
0>
Посмотрите в ВИДЕОУРОКЕ подробное решение уравнения
Источник
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Источник
Видеолекция «Решение показательных уравнений и неравенств»
В видеолекции «Решение показательных уравнений и неравенств»показаны основные принципы решения всех типов показательных уравнений и неравенств. Я подробно рассказываю, как распознавать тип показательного уравнения и какие алгоритмы применять при решении уравнений и неравенств данного типа.
В видеолекции решены 13 уравнений и неравенств, начиная с не сложных, и заканчивая задачами уровня Задания 15.
Решение каждого задания представляет собой пошаговый разбор с подробными комментариями. Для самостоятельного освоения этой темы желательно сначала посмотреть видеолекцию, а потом попробовать решить эти же уравнения самостоятельно, используя презентацию. С помощью презентации вы можете продолжить решение задачи самостоятельно с любого шага решения.
В видеолекции подробно объяснено решение уравнений и неравенств:
1. Решить уравнение:
2. Решить неравенство:
=0,2″ title=»5^<
3. Решить уравнение:
4. Решить неравенство:
5. Решить уравнение:
6. Решить неравенство:
7. Решить уравнение:
8. Решить неравенство:
=4*9^<
9. Решить уравнение:
10. Решить неравенство:
=<<(sqrt<5>-1)^<2x+1>>/<16^x>>» title=»4*(sqrt<5>+1)^<<6x-3>/
11. Решить неравенство:
12. Решить неравенство:
=3^
13. Решить неравенство:
=0″ title=»sqrt<8-2x-x^2>(4^x-4^<4-x>-68)>=0″/>
Источник
