Способы решения олимпиадных задач физике

10 шагов до высшего балла: алгоритм решения олимпиадных задач по физике

Экзамены и итоговые проверочные будут ждать школьников ещё целый год, а олимпиады ждать не будут. К ним тоже надо готовиться. Наш блогер, учитель физики Филипп Белов, делится своим алгоритмом решения задач повышенной сложности по физике.

Когда школьники седьмого класса, заинтересовавшись физикой, начинают путь по дороге олимпиадного движения, они сталкиваются с тем, что задачи, предлагаемые на всех уровнях разных олимпиад, чаще всего серьёзно отличаются от обычных задач на уроках. Их структура, постановка вопросов и требований чаще всего не вписываются в стандартную схему решения и оформления задач, с которой знакомят учителя физики на первом этапе изучения предмета.

Эта особенность требует специального внимания руководителя кружка по физике. Оставляя общий подход решения и оформления олимпиадных задач без комментариев и сосредотачиваясь исключительно на решении как можно большего объёма вариантов олимпиад прошлых лет, мы рискуем получить олимпиадника, который умеет решать нестандартные задачи, но не в состоянии грамотно выразить свои мысли на бумаге.

Можно выделить некоторую последовательность действий, которую стоит показать детям на первых занятиях кружка и учитывать при разборе отдельных задач, демонстрируя варианты реализации отдельных пунктов.

1. Записываем краткое условие, размышляем над размерностями

Запись краткого «Дано», как в обычных задачах, на олимпиаде, безусловно, не требуется. Можно сразу приступать к решению, но перевод текстового условия в математический вид нельзя считать бесполезным. Структурирование, выбор обозначений для отдельных величин и анализ текста задачи — важный первый шаг на пути к решению.

Перевод размерностей в СИ тоже не только не обязателен, но часто вреден. Иногда удобнее задачу решать во внесистемных единицах. Тем не менее решить, стоит ли переводить размерности или нет, необходимо на первом этапе анализа задачи.

2. Делаем чертёж, если это возможно

Большинство задач разных разделов физики допускает возможность изображения какого-либо графического варианта описания задачи. Даже если в условии этого не требуется, рисунок часто оказывается полезным.

3. Выделяем основную идею (идеи)

Для выбора методов решения и подходящих законов необходимо осознать основную идею, которой посвящена задача. Это могут быть особенности какого-то конкретного процесса, интегральные связи между различными разделами физики или принципы работы какого-то устройства.

4. Записываем базовые формулы или законы, которые планируем использовать

Желательны ссылки на названия законов. Перечисление тех соотношений, которые будут использоваться для решения, убережёт от ошибок алгебраических преобразований, тем более обидных в случае, когда правильна вся физика задачи, но ошибочна математика.

5. Описываем введение новых и неизвестных переменных

Иногда школьники об этом забывают. Вводя нестандартные обозначения используемых величин, при первом упоминании следует указать, что именно этой буквой обозначается. При проверке работы, безусловно, эксперт в состоянии догадаться о смысле неописанных величин, но когда этих переменных много, а их формат сильно разнится с общепринятым, то необходимость догадок не только серьёзно затрудняет проверку, но и порой вводит в заблуждение.

6. Работаем с алгебраическими преобразованиями

В редких случаях, когда они не нужны, сразу делаем расчёты. Ребята серьёзного уровня подготовки многие преобразования могут делать устно. Однако пропуск важных логических переходов допустим только при крайне объёмном решении и не должен влиять на восприятие решения в целом.

7. Получаем итоговые результаты в численном виде

Расчеты искомой величины — важный, но не последний этап решения. Оставшиеся позиции представленного алгоритма могут быть опущены для решения задач базового курса физики, но при работе с примерами повышенного уровня сложности после получения ответа следует перейти к его анализу.

8. Рассуждаем о разумности (адекватности, соответствии условию задачи) результата

По возможности ищем второй способ решения с целью проверки. Если второго способа решения нет, то, как минимум, делаем проверку любым доступным путём.

9. Размышляем, сколько возможно вариантов решения в поставленных условиях

Нет ли иных вариантов протекания процесса? В случае, если задача подразумевает несколько возможных веток решения, то полный балл за её решение можно получить только в случае описания всех направлений.

10. Записываем ответ

Только после выполнения первых девяти пунктов переходим к записи ответа и завершению задачи.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Источник

Методика решения олимпиадных задач

Просмотр содержимого документа
«Методика решения олимпиадных задач»

Методика подготовки учащихся к олимпиадам по физике.

В период ускорения научно-технического прогресса на каждом рабочем месте необходимы умения ставить и решать задачи науки, техники, жизни. Поэтому, целью физического образования является формирование умений работать со школьной учебной задачей. Решение же конкурсных задач по физике основано на практико-ориентированном подходе. Знание теорий необходимо, но не достаточно, и причина этого в том, что умение решать задачи по физике требует не только конкретных знаний, но в большей степени знаний обобщённых, которые приобретаются только на опыте, в процессе решения большого количества задач. Отсюда, и это едва ли не главное условие обучения,- необходимо время для приобретения этого опыта. Практика показывает, что не менее года систематических дополнительных специальных занятий необходимо провести с ребёнком, прежде чем можно будет с надеждой на успех направить его на олимпиаду по физике. Поэтому начинать подготовку к олимпиаде по физике учащегося, у которого определился интерес и способности к изучению физики, желательно уже с 7 класса. Причём дополнительные занятия с одарёнными ребятами должны быть не только постоянными в течение всего учебного времени, не должны они прерываться и во время школьных каникул. Дополнительные занятия с одарёнными ребятами должны проводиться в строгом соответствии с составленной программой. Бессистемные занятия по решению задач повышенной трудности чаще всего ничего или почти ничего не дают. Отличительной особенностью подготовки к олимпиаде по физике является её комплексность. Это не просто дополнительные занятия по углубленной программе. В отличие от других предметов, подготовка к олимпиаде по физике требует обязательного расширения и углубления знаний практически всех, изучаемых в школе разделов математики, знания основ строения вещества, изучаемого в химии, основ информатики, а также приёмов развития памяти и методов запоминания.

Это должен быть комплекс взаимосвязанных тематикой и временем изучения программ по математике, физике, химии и информатике. Именно такое сочетание даёт достаточно быстрое и качественное овладение приёмами и методами решения физических задач. Любое решение физической задачи предполагает три обязательныхэтапа:

— физический – он заключается в анализе процесса или явления и составлении замкнутой системы уравнений;

— математический – получение решения этой системы в общем и числовом виде;

— заключительный – анализ решения с физической точки зрения.

Поэтому решение задач по физике требует очень глубоких знаний практически всех разделов математики. Все проводимые олимпиады по физике показывают, что учащиеся не справляются с математической частью физических задач, в особенности, если требуется знание геометрии или тригонометрии.

Олимпиады различного уровня предназначены для выявления одарённых учащихся. В олимпиадах выигрывают те учащиеся, которые могут нестандартно мыслить, отходить от общепринятых методик решения задач, находить оригинальные подходы для выявления истины. Однако без соответствующей теоретической и практической подготовки олимпиаду не осилить.

Олимпиадные задания можно разделить на два типа:

К данной группе относятся качественные задания и задачи, решаемые стандартным способом с помощью формул и математических преобразований. Здесь требуются хорошая теоретическая подготовка учащихся, а также умение быстро делать математические преобразования, приводящие к получению расчётной формулы. В школе мы решаем задачи с большими погрешностями и допусками. Например, пренебрегаем трением, не учитываем сопротивление проводов, используем понятие идеального газа, в олимпиадной же физике часто встречаются задачи, где рассматриваются реальные физические объекты. При решении таких задач от учеников требуются навыки исследовательской работы, а также умения субъективно оценивать происходящие процессы, описанные задачи.

Экспериментальные задания можно разделить на несколько групп:

задачи с «чёрным ящиком». Требуется по каким – то исследованиям

узнать, что находится в закрытой коробке;

измерение параметров и расчёта какой-то физической величины;

исследование функциональных зависимостей физических величин;

конструирование действующей модели технического устройства.

Для решения экспериментального задания от учащихся требуются знания

о свойствах материалов, умения работать с инструментами и приборами. Необходимо научить школьников работать с приборами, которые в школе не применяются. Например: штангенциркуль, микрометр, ареометр, мультиметр и т.д.

Рассмотрим пример решения теоретического задания:

С какой скоростью и по какому курсу должен лететь самолёт, чтобы за 2 ч. пролететь на север 300 км, если во время полёта дует северо-западный ветер под углом 30° к меридиану со скоростью 27 км/ч?

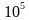
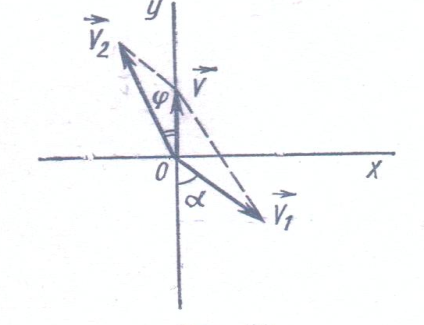
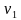
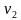
3* м

рис. 1

= 27км/ч

– ?, φ — ?

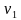
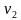
Рассмотрим движение самолёта в системе отсчёта, с землёй. Проведём ось ОХ в направлении на восток, а ось ОY – на север (рис. 1). Тогда скорость движения самолёта в выбранной системе отсчёта v = + ,где v = l/t.

Запишем уравнение в проекциях на оси ОХ и ОY:

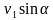
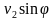
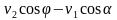
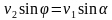
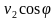
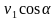
0 = — ,v = ,

, = + v.

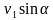
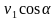
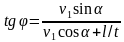
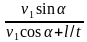
Разделив полученные уравнения, получим tgφ = / ( + v), или с учётом v = l/t

; φ = arctg ;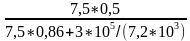

φ = arctg ≈ 0,078 рад.

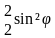
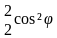
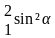
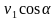
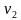
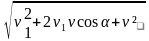
Возводя в квадрат правые и левые части уравнений, и складывая полученные выражения, находим v + v = v + ( + v)², откуда

= ,

или с учётом v = l/t

≈

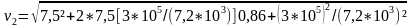
Среди теоретических задач можно выделить задачи на применение формул. Часто оказывается, что какая-либо тема очень проста с точки зрения физики, а это значит, что её изучают в школе очень подробно, на множестве примеров и со множеством (достаточно простых) формул. Типичный пример такой темы: кинематика тела, брошенного под углом к горизонту. К сожалению, зачастую у учащегося создаётся впечатление «мешанины формул», и он не понимает, какие именно из кучи известных формул надо записывать в том или ином случае. Задачи из этой серии как раз проверяют способность школьника чувствовать, что стоит за каждой формулой, какие формулы относятся к предложенной задаче, а какие нет. Обычно такие задачи не представляют математической сложности: после записи нужной системы уравнений задачи решаются быстро. Трудность заключается в аккуратном выписывании формул.

Тело брошено вертикально вверх с некоторой скоростью. В тот момент, когда оно достигло наивысшей точки, которая располагается на высоте h над землёй, вслед за ним с той же самой начальной скоростью было брошено второе тело. На какой высоте тела столкнуться? Размерами тел и сопротивлением воздуха пренебречь.

Движение тела, брошенного вертикально вверх,- равно ускоренное движение повертикальной прямой с ускорением g, направленным вниз (то есть в обычной системе координат, где ось y направлена вверх, ускорение отрицательное). Уравнение движения такого тела, брошенного с высоты со скоростью

Пишем уравнения движения для обоих тел, причём оба эти уравнения должны выражаться через одно и то же время. Проще всего взять за начало отсчёта времени тот момент, когда было выпущено второе тело.

Тогда = h — gt²/2; = *t-gt²/2.

Столкновение тел происходит в тот момент, когда координаты тел совпадут. Так что нам осталось приравнять , найти t, затем подставит его в любое из двух уравнений и найти искомую высоту. 3/4 h.

Или можно поступить чуть хитрее и воспользоваться тем, что движение обоих тел абсолютно одинаковое, но только сдвинутое по времени на величину τ= . Тогда =h — gt²/2; = h – g (t- τ)²/2.

Приравнивание сразу даёт t=τ/2, а подстановка в любое из уравнений даёт ответ 3/4 h.

Эта задача довольно простая, поскольку она касается равноускоренного одномерного движения, и как олимпиадную её можно предлагать на уровне школьных или городских олимпиад.

Задачи на физический смысл и применимость законов.

Как правило, те или иные законы выполняются не всегда, а при соблюдении некоторых условий. Эти условия школьнику сообщаются мимоходом, и зачастую он их забывает, запоминая лишь формулу. Задачи на применимость законов – это как раз задачи на проверку того, понимает ли школьник физический смысл и границы применимости тех или иных законов. Часто такие задачи формулируются в виде «парадокса», и от школьника требуется его распутать.

По дороге с постоянной скоростью едут две машины. Они едут по инерции: никакого сопротивления своему движению они не испытывают. Одна из машин тратит определённое количество бензина и разгоняется до скорости 2v, и снова едет по инерции с этой новой скоростью. В процессе разгона химическая энергия, запасённая в бензине, тратится на изменение кинетической энергии автомобиля. Однако в одной системе отсчёта (связанной с неподвижным пешеходом) это изменение равно 3/2mv², тогда как в другой системе отсчёта (связанной со вторым автомобилем) она равна mv²/2. Но ведь химическая энергия, запасённая в бензине, не зависит от системы отсчётов. Как разрешить парадокс?

Опыт показывает, что многие не понимают, в чём тут проблема. Говорят, ну так это понятно: в одной системе отсчёта кинетическая энергия одна, в другой – другая, в чём проблема? Проблема в том, что в задаче речь идёт не про саму кинетическую энергию, а про её изменение. А оно, в силу закона сохранения полной энергии, не должно меняться при переходе от одной инерциальной системы отсчёта в другую.

Для того, чтоб ещё сильнее почувствовать парадокс, можно рассмотреть процесс разгона машины в третей системе отсчёта, которая всегда двигалась со скоростью 2v. Тогда в этой системе отсчёта машина тратит какое-то количество химической энергии для того, чтобы уменьшить свою кинетическую энергию. Законом сохранения энергии и не пахнет. В чём же дело?

Дело в том, что закон сохранения энергии справедлив лишь для замкнутой системы, т.е. системы, не взаимодействующей с внешним миром. Никто не требует сохранения энергии для части системы. Наша машина-незамкнутая система, потому что она разгоняется. Замкнутая система разгоняться не может по первому закону Ньютона.

С чем же взаимодействует машина? С тем, от чего она отталкивается при разгоне (ведь разгон, т.е. ускорение, возникает, согласно второму закону Ньютона, из-за внешних сил). Поскольку машина разгоняется из-за того, что её колеса имеют сцепление с Землёй, то отталкивается она от Земли. Итак, становится ясно, сто машина – это лишь часть взаимодействующей системы «Земля – машина», и потому кинетическая энергия одной только машины не обязана сохраняться, что мы и видим в нашем «парадоксе».

А сохраняется ли энергия всей системы «Земля – машина»? Разумеется, да, поскольку это замкнутая система.

Часто встречаются задачи, в которых, казалось бы, ничего не дано, а что-то требуется найти. Эти задачи могут легко поставить школьника в тупик: с чего начинать решение, если ничего не дано?!

Метод решения стандартен: необходимо научиться преодолевать страх перед неизвестным. Это значит, что в начале решения надо ввести все

необходимые параметры. Да, они не даны, и ответ выражать через них нельзя,

но никто нам не запрещает их использовать в процессе решения! Оказывается,

что в ответе все неизвестные введенные величины сокращаются.

Такие задачи красивы с точки зрения физики, поскольку они используют

Неочевидную симметрию системы: ответ не зависит от конкретного выбора

параметров, а значит годится для целого класса систем. Составление таких

задач — чрезвычайно хорошая проверка для преподавателя-физика, поскольку

он обязан почувствовать, увидеть систему со скрытой симметрией.

Оцените длину шкурки, которую снимают, почистив один килограмм картошки. Килограмм какой картошки можно быстрее почистить: крупной или мелкой? Отдельно рассмотрите предельный переход к случаю очень мелкой картошки.

Вначале проанализируем задачу в общем виде.

Пусть картофелины имеют форму шара радиус R и плотность ρ, ширина снимаемой шкурки h. Тогда длинна шкурки, снимаемой с одной картофелины =4πR²/ h, а с одного килограмма – l= / πρR³ = 3/ρRh.

Таким образом, длина снимаемой с одного килограмма картофеля шкурки обратно пропорционально радиусу (т.е. характерному размеру) картофелины. Поэтому килограмм мелкой картошки очистить дольше, чем крупной. Из этой формулы следует, что в случае очень мелкой картошки длина снимаемой шкурки должна становиться бесконечно большой (для оценки можно использовать следующие числовые значенияρ=1000кг/м³, R=3см, h=1см, то получаем l=10м).

Ответ: 10 метров.

На столе лежит книга размером 1х1. Наименьшая работа, необходимая для того, чтобы раскрыть её на середине равна А. Сколько вести книга?

Минимальная работа, необходимая для раскрытия книги посередине равна работе подъёма половины массы книги на высоту h/2. А= *g* . Отсюда находим массу книги m= .

Методика решения качественных задач.

Под качественными задачами, понимают задачи, решение которых не требует математических операций и вычислений.

Это задачи на объяснение. Они отличаются от количественных или расчётных задач тем, что в них меньше ориентиров для выдвижения гипотез.

Выявление ориентиров, т.е. существенных признаков объектов и явлений, осуществляется с помощью переформулирования и перемоделирования. Если эти операции в процессе обучения не развивают должным образом, качественные задачи воспринимаются как более трудные.

Прямой вопрос качественной задачи – это в большинстве случаев вопрос о соотношении каких – либо величин.

Дайте физическое обоснование пословице: «Коси коса пока роса, роса долой и мы домой».

Роса увеличивает массу стебля. Поэтому, при ударе косой он в меньшей мере изгибается, и коса сразу срезает его.

Роса создаёт смазку и уменьшает силу трения, когда при обратном движении косы она скользит по траве.

Почему нельзя прикасаться к неизолированным электрическим проводам голыми руками?

Влага на руках всегда содержит раствор различных солей и является электролитом. Поэтому она создаёт хороший контакт межу проводами и кожей.

Почему радуга имеет форму дуги?

Радуга возникает в следствие полного отражения и дисперсии лучей в дождевых каплях. При этом цветные лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей. Геометрическое место точек, дающих лучи, направленные под углом 42° представляют дугу окружности.

В олимпиаде по физике обязательно включаются задачи, приближенные к практике, родившиеся под влиянием реального физического эксперимента при наблюдении природы и т.д. В таких задачах, как правило, рассматриваются физические объекты; их решения часто имеют одиночный характер. Они чрезвычайно важны для развития физического способа мышления. И зачастую вызывают у школьников большие затруднения, чем теоретические задачи.

На какую глубину в водоёме надо погрузить детский резиновый мячик, чтобы он начал тонуть?

При постоянной температуре: pv= , где = π * R³ — объём мяча.

P = ρgh+ 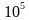— давление на глубине h;

m = * =– масса резинового мяча.

Условие равновесия: mg = ρg ( +v), тогда h= = , где

= 1,5* 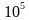Па, ρ = 10³ кг/м³ , m = 0,5кг, R = 0,1м, h = 240м.

Источник