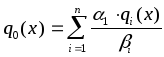Способы решения однокритериальных задач

1.5.1. Однокритериальные задачи принятия решений.

Критерию q(x) может придаваться различный смысл, но почти всегда его можно интерпретировать как выигрыш или проигрыш, который получает лицо, выбравшее альтернативу х из множества альтернатив Х. Если последствия выбора альтернативы х известны точно, т.е. выбор детерминированный, то сравнение альтернатив в этом случае сводится к сравнению соответствующих чисел. Заметим, что введенное соответствие задает функцию q(x) на множестве альтернатив Х.

В этом случае принятие решения сводится к выбору оптимальной (наилучшей) альтернативы х из множества альтернатив Х.

Определение 1: Наилучшей (оптимальной) альтернативой xX называется такая альтернатива, которая обеспечивает минимальное значение критерия (проигрыша) при выборе альтернативы х:

x = argmin q(x), xX

Если по своему содержанию критерий q(x) характеризует выигрыш, то наилучшей должна быть альтернатива, которая обеспечивает максимум критерия выигрыша.

Такие задачи принятия решений называются оптимизационными. Для их решения разработано множество различных методов одномерной и многомерной оптимизации, которые достаточно подробно описаны в литературе. Укажем наиболее распространенные из них. Среди методов одномерной оптимизации к самым распространенным относятся методы бисекции, золотого сечения, ломаных. При решении задач многомерной оптимизации обычно используют методы линейного программирования (в том числе различные модификации симплекс-метода), различные варианты градиентных методов, вариационные методы, методы динамического программирования. Все эти методы математически формализованы. Их разработкой и обоснованием занимается специальный раздел математики, который называют обычно “методами решения экстремальных задач” или “методами оптимизации”.

В случае, если последствия выбора альтернативы х из множества альтернатив Х точно не известны, но известны вероятности их появления p(x), то принятие решений обычно сводится к выбору альтернативы х, удовлетворяющей принципу «наименьшего гарантированного проигрыша» или «наибольшего гарантированного выигрыша». Разработкой методов принятия решений в таких ситуациях занимаются в разделах математики, называемых «теорией игр» и «исследованием операций».

1.5.2. Многокритериальные задачи принятия решения.

В случае многокритериальной задачи принятия решения совсем не тривиально определить, что есть «оптимальное» решение. Поясним это на примере. Пусть мы покупаем подарок, который характеризуется тремя критериями: ценой, временем, затрачиваемым на его покупку, полезностью. Естественно, что нам хотелось бы, чтобы цена и время были минимальными, а полезность — максимальной. Но в случае многокритериальных задач, критерии могут быть противоположны друг другу (как в нашем случае, например, время – деньги). Поэтому бессмысленно принимать за оптимальное решение ту альтернативу, на которой достигается экстремальное значение всех критериев.

К сожалению, единой трактовки термина «оптимальное» решение в случае многокритериальных задач не существует. Однако существует четыре основных подхода к введению понятия «оптимальный» в этом случае.

Разделим все задачи многокритериального выбора на два класса: задачи принятия решений с равнозначными критериями и задачи принятия решений с неравнозначными критериями (т.е. существует некоторый приоритет одних критериев над другими).

Рассмотрим вначале более простой в некотором отношении случай — неравнозначных критериев.

Предположим, что есть n критериев: q₁. q_n. Эти критерии можем упорядочить. Причём каждому критерию мы можем приписать не только порядковый номер, но и вес, т.е. некоторое числовое значение, определяющее превосходство этого критерия над остальными. В этом случае на основе существующих критериев мы можем ввести новый критерий q₀, который принято называть суперкритерием. Самым распространенным способом введения суперкритерия является аддитивный:

Здесь _i – вес критерия q_i(x), а _i — коэффициент, снимающий размерность (чтобы можно было складывать «землекопов» с «лопатами»).

Пример.В задаче выбора подарка оставим два критерия:q₁— цена подарка, главный критерий;q₂— время. Договоримся, что 1 час = 60 руб. В нашем случаеq₀(x) =q₁(x)/руб. + 60q₂(x)/час. Допустим, что нам надо выбрать наилучший из трех подарков: цена первого, второго и третьего соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин. Посчитаем значение суперкритерия для каждого из подарков:

q₀(x1) = 300 + 60*2 = 420;

q₀(x2) = 350 + 60*1 = 410;

q₀(x3) = 400 + 60*0,5 = 430

Из сравнения суперкритериев видно, что наилучшим будет второй подарок.

После введения суперкритерия многокритериальная задача стала фактически однокритериальной задачей. Примеры введения суперкритерия мы часто можем наблюдать в спортивных состязаниях. Например, лыжные двоеборцы сначала прыгают на лыжах с трамплина (результат меряется в метрах, а потом в баллах), а потом бегут на лыжах дистанцию 15 км. (результат меряется в сек.) При определении победителя приравнивают 1 балл к 1 сек. У биатлонистов в гонке на 20 км. у мужчин 1 промах (критерий точности стрельбы) приравнивается к 1 мин. штрафа в беге по дистанции (критерий – скорость). Можно встретиться с таким подходом при определении, например, лучшего ученого года в Оренбургской области: 1 изданный учебник приравнивается в баллах к 3 защищенным под руководством данного ученого кандидатским диссертациям или к 1 докторской диссертации.

простота вида суперкритерия.

этот метод и само оптимальное решение существенно зависят от точности определения весовых коэффициентов _i;

вводится дополнительный критерий – суперкритерий, который иногда сложно интерпретировать содержательно.

Последнее легко пояснить на рассмотренном выше примере. Если бы мы оценили 1 час времени в 40 руб., то значение суперкритериев было бы следующим:

q₀(x1) = 300 + 40*2 = 380;

q₀(x2) = 350 + 40*1 = 390;

q₀(x3) = 400 + 40*0,5 = 420

Как видно, в этом случае наилучшим был бы первый подарок. А если бы 1 час времени оценивался в 100 руб., то наилучшим был бы третий подарок.

Метод условной оптимизации.

Этот метод, также как и метод суперкритерия, предполагает, что критерии не равнозначны. Мы можем выбрать самый значимый для нас критерий, но не можем оценить вес каждого критерия численно (не можем сказать, сколько рублей стоит 1 час). В этом случае в качестве единственного критерия мы оставляем самый значимый для нас критерий, а остальные критерии считаем ограничениями (условиями). Далее различают два случая введения ограничений: типа равенств и типа неравенств. Первый случай проще осуществляется технически, но менее адекватен реальности. Второй более адекватен реальности, но труднее осуществляется технически.

Пример. Как и в предыдущем примере будем выбирать лучший подарок по двум критериям: q₁ — цена подарка, главный критерий; q₂ — время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение, 2 часа, 1 час и 30 мин.

Рассмотрим случай ограничений типа равенств. Зададим ограничение по времени (так как это не главный для нас критерий): время, затрачиваемое на приобретение подарка q₂ = 1 час. 20 мин. Выберем теперь из всех подарков такие, у которых q₂ = 1 час. 20 мин. Видим, что таких подарков в нашем списке нет. Таким образом, далее мы осуществляем выбор на пустом множестве альтернатив. Это значит, что мы отвергли все предложенные альтернативы.

Естественно, что в реальных ситуациях принятия решений ограничения типа равенств встречаются не часто. Более адекватный случай – ограничения типа неравенств. Зададим в нашем примере ограничения типа неравенств. Будем считать, что нам надо купить подарок не ровно за 1 час. 20 мин. (как это было в ограничении типа равенств), а не более, чем за 1 час 20 мин., т.е. 0 мин. q₂ 1 час 20 мин. Выбираем из всего множества подарков те, которые покупаются не более, чем за 1 час 20 мин. В это множество вошли второй и третий подарок. Теперь мы выбираем из них наилучший на основании только главного критерия – цены. Наилучшим будет второй подарок, т.к. у него меньшая цена (350 руб.)

не вводится никаких новых критериев;

выявляется только самый значимый критерий, но численные значения весов не определяются.

ограничения типа равенств часто являются неадекватными реальным ситуациям принятия решений;

с ограничениями типа неравенств часто технически сложно решать задачу принятия решений.

На практике при решении многокритериальных задач выбора при неравнозначных критериях часто пользуются методом уступок. Как и в методе условной оптимизации, выбирают главный критерий. Далее задают значение вспомогательного критерия. После этого при фиксированном значении вспомогательного критерия ищут альтернативу с оптимальным значением главного критерия. Если значение главного критерия удовлетворяет лицо, принимающее решение, то найденная альтернатива принимается. Если значение главного критерия не удовлетворяет лицо, принимающее решение, то он пытается «уступить», т.е. снизить значение второстепенного критерия в надежде получить выигрыш в значении главного критерия. Если при сделанной уступке лицо, принимающее решение не выигрывает в значении главного критерия, то он либо продолжает процесс уступок, либо принимает какое-то решение из предыдущих, либо отвергает все альтернативы.

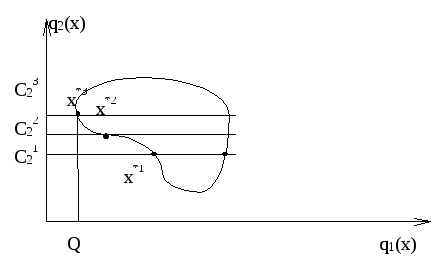
Поясним суть этого метода на рисунке. Пусть q₁(x) — главный критерий. Зафиксируем значение второстепенного критерия q₂(x) = C₂ 1 . При данном фиксированном значении этого критерия (на рисунке это нижняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q₁(x). Это точка x₁ *1 . Предположим, что значение главного критерия q₁(x₁ *1 ) нас не удовлетворяет.

Мы делаем уступку в значении второстепенного критерия q₂(x), полагая его значение q₂(x) = C₂ 2 > C₂ 1 . Далее при этом значении критерия q₂(x) (на рисунке это средняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q₁(x). Это точка x₁ *2 . Предположим, что значение главного критерия q₁(x₁ *1 ) нас не удовлетворяет.

Мы готовы сделать еще уступку в значении второстепенного критерия q₂(x), полагая его значение q₂(x) = C₂ 3 > C₂ 2 . Далее при этом значении критерия q₂(x) (на рисунке это верхняя из горизонтальных прямых) найдем альтернативу с минимальным значением критерия q₁(x). Это точка x₁ *3 . Значение главного критерия q₁(x₁ *3 ) = Q нас теперь удовлетворяет. На этом процесс поиска решения прекращается. Найденная альтернатива x₁ *3 считается принятой.

Пример. Выбираем лучший подарок по двум критериям: q₁ — цена подарка, главный критерий; q₂ — время, затрачиваемое на его приобретение. Допустим, что цена первого, второго и третьего подарков соответственно 300 руб., 350 руб. и 400 руб.; время, затрачиваемое на их приобретение 2 часа, 1 час и 30 мин.

Зафиксируем значение второстепенного критерия q₂(x) = 20 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это множество пусто. Такое положение нас не удовлетворяет. Сделаем уступку по времени. Положим q₂(x) = 30 мин. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок третий. Посмотрим значение главного критерия – цену. Допустим, что его цена 400 руб. нас не устраивает. Вновь делаем уступку по времени. Положим q₂(x) = 1 час. При этом значении второго критерия выберем подарок с наименьшей ценой. Это подарок второй. Посмотрим значение главного критерия – цену. Допустим, что его цена 350 руб. нас устраивает, т.е. мы считаем цену нашей уступки по времени (30 мин.) адекватной цене нашего выигрыша в главном критерии (50 руб.). Тогда процесс выбора окончен. Мы выбираем второй подарок.

идея метода уступок крайне проста;

метод прост в реализации.

метод не гарантирует, что за достаточно большое число шагов найдётся удовлетворяющее решение. Это возможно из-за того, что цена уступок не будет адекватной цене нашего выигрыша.

Все предыдущие методы относились к случаю, когда критерии были неравнозначные. Остановимся теперь на случае равнозначных критериев. В этом случае критерии нельзя не только упорядочить между собой, но даже выделить главный среди них. В этой ситуации оптимальные решения образуют паретовское множество (множество оптимальных по Парето решений), т.е. множество альтернатив, не сравнимых между собой.

Альтернативы x, y называются несравнимыми между собой, если по одному критерию q₁ первая альтернатива хуже второй (q₁(x) > q₁(y)), а по другому критерию q₂ первая альтернатива лучше второй (q₂(x) 27 / 30 27 28 29 30 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Однокритериальные и многокритериальные задачи оптимизации

Задача выработки решения в условиях определенности характеризуется отсутствием случайных и неопределенных факторов. Поэтому каждая стратегия u приводит к вполне определенному исходу g = W(u) и схема модели проблемной ситуации приобретает вид

Одни исходы с точки зрения лица, принимающего решение, могут быть лучше или хуже других. Поэтому будем считать, что на множестве исходов G существует структура предпочтений ЛПР, представленная отношениями нестрогого предпочтения R, строгого предпочтения Р и безразличия I. В общем случае R — частичный квазипорядок, Р — строгий частичный порядок, I — эквивалентность. Как уже отмечалось, эта структура может окончательно сложиться в ходе анализа рассматриваемой задачи принятия решения, и исследователю заранее обычно неизвестна (или известна не полностью). Предположим, что на основе полученной информации W о предпочтениях ЛПР построена модель его предпочтений P в виде отношений нестрогого предпочтения R(W), строгого предпочтения P(W) и безразличия I(W) на множестве исходов G. Поскольку каждой стратегии соответствует вполне определенный исход, то эти отношения естественным образом порождают аналогичные по смыслу отношения R_W , Р_W и I_W во множестве стратегий U:

Например, во второй из этих трех строк записано, что стратегия u предпочтительнее стратегии u, когда исход Y(u) предпочтительнее исхода Y(u). Если же во множестве G на основе информации W удалось построить функцию ценности f W (g), то и на множестве стратегий оказывается заданной функция ценности F W (u)=f W (Y(u)).

Таким образом, в задачах принятия решений в условиях определенности задание отношения R(W) позволяет естественно и просто ввести следующий принцип оптимальности: оптимальной может быть лишь Р_W — максимальная (т.е. неулучшаемая по Р_W) стратегия. Если отношение R_W оказывается связным, то этот принцип выделяет множество U_W стратегий, наилучших по R_W, любая из которых может быть взята в качестве оптимальной. В частности, при наличии функции ценности f W оптимальной будет всякая стратегия u * , максимизирующая F W :

F W (u * ) = F W (u)

Если же R_W несвязно, то не все P_W — максимальные стратегия могут быть эквивалентными, и тогда для осмысленного выбора оптимальной стратегии из множества U_W всех Р_W -максимальных необходимо использовать дополнительную информацию о предпочтениях.

Однокритериальные задачи оптимизации.

Если на множестве исходов G задан критерий эффективности K(g), то с его помощью можно характеризовать непосредственно сами стратегии: стратегии и будет соответствовать значение критерия K(Y(u)). Поэтому в задачах выработки решений в условиях определенности под критерием можно понимать числовую функцию К(u), определенную на множестве стратегий U.

Если эффективность стратегий удается достаточно полно оценить при помощи одного критерия, то такие задачи называются однокритериальными.

Выбор (построение) единственного критерия эффективности должен осуществляться с учетом ряда специальных требований. Обычно считается, что должны выполняться следующие требования.

а) Соответствие. Критерий должен соответствовать смыслу (существу) поставленной задачи.

б) Полнота. Критерий должен обладать функциональной полнотой (т.е. учитывать все существенные для решения поставленной задачи военно-технические, экономические и другие факторы).

в) Критичность. Критерий должен быть достаточно чувствительным к переменным параметрам задачи.

г) Содержательность. Критерий должен иметь «физический смысл» (это упрощает анализ и интерпретацию полученных результатов и формулировку рекомендаций).

д) Вычислимость. Значения критерия должны достаточно просто вычисляться (это обеспечивается, например, представлением критерия относительно простым аналитическим выражением).

В большинстве практических задач в качестве критерия выбираются такие функции, для которых либо большее значение всегда предпочтительнее меньшего, либо, наоборот, меньшее значение предпочтительнее большего. В первом случае критерий часто имеет смысл прибыли, дохода и т.п., выражает степень достижения поставленной цели (например, процент выполнения планового задания) или же отражает «технические» характеристики, которые желательно увеличивать (скажем, удобство работы оператора, которое может оцениваться экспертами в баллах). Во втором случае критерий имеет смысл издержек, расхода ресурсов и т.п. или же описывает «технические» характеристики, которые желательно минимизировать (скажем, шумы двигателя подводной лодки).

В однокритериальной задаче при указанном направлении предпочтительного изменения значений критерия фактически оказывается введенной функция ценности, и понятие оптимальной стратегии определяется очень просто: если большие значения критерия предпочтительнее меньших, то оптимальной является стратегия u * , максимизирующая критерий

;

(1.2)

если же, наоборот, меньшие значения критерия предпочтительнее больших, то оптимальной является стратегия, минимизирующая критерий

.

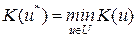(1.3)

Типичным примером однокритериальной задачи выработки решения в условиях определенности является транспортная задача, состоящая в отыскании плана перевозок некоторых грузов за минимальное время (К — время перевозок) или же с минимальной стоимостью (К — стоимость перевозок).

Таким образом, определение понятия оптимальной стратегии в однокритериальных задачах выработки решений в условиях определенности в большинстве случаев никаких принципиальных трудностей не вызывает. Однако это не значит, конечно, что практическое отыскание оптимальной стратегии всегда осуществляется достаточно просто. Наоборот, реальные задачи нахождения (1.2) и (1.3) в вычислительном отношении оказываются обычно весьма сложными, и для их решения приходится использовать ЭВМ и специальные методы оптимизации, выбор которых определяется конкретными особенностями задачи, требованиями к точности решения, наличием времени и т.п.

Не следует, однако, думать, что всякая однокритериальная задача легко представляется в виде задачи максимизации или же минимизации путем задания единого направления возрастания предпочтений для всей шкалы критерия. Иногда для такого представления может потребоваться более тонкая информация о предпочтениях. Для иллюстрации разберем следующий пример.

Пусть t * — установленное время выполнения боевой задачи, причем нежелательно ни преждевременное ее выполнение, ни выполнение с опозданием. В этом случае на шкале критерия K=t имеются два направления возрастания предпочтений (рис. 1.1) и поэтому необходима дополнительная информация о предпочтениях для сопоставления отклонений t-t * разных знаков. В частности, если установлено, что отклонения, различающиеся лишь знаками, одинаковы по предпочтительности, то исходную задачу с критерием K=t можно представить в виде задачи минимизации нового критерия К‘ = |t — t * |.

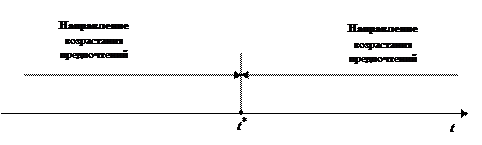Многокритериальные задачи оптимизации.

На практике далеко не всегда удается найти единственный критерий, удовлетворяющий перечисленным выше требованиям (и даже всего лишь первым двум из них). Поэтому во многих задачах выработки решений ограничиться одним критерием эффективности не удается, и приходится рассматривать целую совокупность критериев K₁, . К_m, образующих векторный критерий К = (K₁, . К_m). Такие задачи называются многокритериальными, а критерии K_i — частными (или локальными) критериями.

В многокритериальной форме естественным образом формулируются задачи, когда понятие эффективности оказывается сложным (составным) и расчленяется на ряд более простых понятий, с каждым из которых оказывается связанным свой критерий.

Векторные критерии естественным образом появляются:

— при необходимости определения как потребного количества ресурса (средств), так и рационального способа его использования в таких задачах один критерий (пусть К₁) характеризует количество ресурса, другой (К₂) — результат его использования. Примером может служить задача проектирования автомашины для перевозки спецгруза, характеризуемой стоимостью производства и эксплуатации (К₁) и максимальной длиной пробега (К₂);

— при неоднородности ресурсов, требующихся для достижения поставленных целей: К_i — количество «ресурса» i-го типа. Примером является задача планирования комплексной научно-исследовательской работы специалистов разных профилей;

Для примера рассмотрим более подробно источники многокритериальности задач целераспределения. На практике применяются Различные математические постановки таких задач. С методической точки зрения удобно выделять прямые и обратные задачи целераспределения. Прямые задачи заключаются в отыскании наилучшего плана удара заданными средствами поражения. Обратные задачи состоят в определении наименьшего потребного Расхода средств (снарядов, мин, ракет и т.п.) для поражения заданного объекта или группы объектов. Очень часто как прямые, так и обратные задачи естественным образом ставятся как многокритериальные. Это связано с целым рядом причин, к основным из которых относятся следующие:

а) сложность и разнородность объектов поражения;

б) необходимость соизмерения ущерба, наносимого противнику, с ущербом, наносимым противником;

в) разнородность средств поражения.

Сложность и разнородность объектов поражения приводят к многокритериальности прямых задач целераспределения. Действительно, прямая задача фактически заключается в отыскании плана нанесения противнику наибольшего ущерба. Поэтому, если величину ущерба удается охарактеризовать одним числом, то задача сводится к максимизации единственного критерия эффективности, в роли которого выступает функция ущерба противнику. Так, для группы однородных малых целей ущерб можно измерять числом пораженных целей. Поэтому в качестве критерия эффективности удара по такой группе можно использовать, например, среднее число пораженных целей. Однако, если объекты поражения неоднородны, то для оценки ущерба приходится использовать, как правило, векторные показатели. Например, если множество всех объектов разбито на m групп однородных объектов, а эффективность удара по i-й группе оценивается одним критерием K_i, то задача целераспределения оказывается многокритериальной.

Необходимость соизмерения ущербов, наносимых в ходе боя противнику и планирующей стороне, приводит к постановке прямых задач целераспределения, особенно крупномасштабных, в многокритериальной форме. Предположим, что ущерб противнику удается оценить всего одним показателем K₁, а ущерб, причиняемый противником планирующей стороне, — одним показателем K₂. При планировании желательно обеспечить возможно большее значение K₁ и возможно меньшее значение K₂. Ясно, однако, что чем больше средств будет выделено для подавления активных объектов (средств поражения) противника, тем меньшее значение примет K₂, но тем меньше будет и значение К₁. Таким образом, задача целераспределения оказывается двухкритериальной.

Требования к набору критериев.

При построении многокритериальной модели проблемной ситуации множество критериев формируется в результате анализа задачи и выявления всех тех свойств исходов, которые характеризуют степень достижения поставленных целей. Построение перечня критериев осуществляется исследователем на основе информации, получаемой от принимающего решение и экспертов. Независимо от конкретного способа формирования набор критериев К₁, . К_m должен удовлетворять определенным требованиям.

а) Соответствие. Набор критериев должен соответствовать смыслу (существу) поставленной задачи.

б) Полнота. Набор из m критериев считается полным, если каждый исход (стратегия) ясно и четко характеризуется совокупностью соответствующих значений критериев. Введение дополнительных критериев в полный набор не должен приводить к изменению решения задач.

в) Минимальность. Набор должен содержать как можно меньшее число критериев. Следовательно, различные критерии не должны характеризовать одно и то же свойство исходов.

г) Операциональность. Каждый критерий должен иметь понятную для принимающего решение формулировку, однозначный и ясный смысл, характеризовать вполне определенное свойство исходов.

д) Измеримость. Каждый критерий должен допускать получение оценки (количественной или хотя бы качественной) интенсивности характеризуемого им свойства.

е) Декомпозируемость. Набор критериев должен обеспечивать возможность упрощения задачи выявления и описания предпочтений на множестве m-мерных векторов, составленных из оценок по всем критериям, путем ее расчленения на отдельные более простые подзадачи.

Очевидно, что перечисленные требования являются противоречивыми в том смысле, что они не могут быть удовлетво­рены все одновременно в наибольшей степени. Например, требование минимальности ориентирует на использование более общих, «агрегированных» критериев, но такие критерии имеют обычно менее ясный и понятный смысл, что противоречит требованию операциональности. Поэтому при формировании набора критериев в практических задачах для удовлетворения сформулированных требований приходится идти на разумные компромиссы.

ГЛАВА 2.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВЫБОРА АЛЬТЕРНАТИВ

Бинарные отношения

Простейшая ситуация, которая позволяет сделать обоснованный выбор из нескольких объектов, возникает, когда задан один «критерий качества», позволяющий сравнить любые два объекта, четко указать, какой из них лучше, и выбрать тот (или те), на котором этот критерий достигает максимального значения. Однако в большинстве реальных ситуаций выделить один такой критерий не удается; более того, часто вообще трудно выделить критерии. Тем не менее для некоторых пар объектов можно указать, какой из объектов пары лучше (предпочтительней другого. В таких случаях говорят, что эти два объекта находятся в бинарном отношении. Понятие бинарного отношения позволяет формализовать операции попарного сравнения. Поэтому оно широко используется в теории принятия решений.

Понятие бинарного отношения

Что такое отношение, проще всего пояснить примерами. Рассмотрим суждения, которые выражают взаимосвязи между не­которыми объектами: «Иван — брат Петра»; «Татьяна старше Александра»; «Киев южнее Москвы»; «Железо тяжелее воды»; «Слово «ночь» и слово «день» содержат одинаковое число букв». Эти пять предложений выражают отношения разного типа. Однако можно заметить сходство в характере отношений, утверждаемых первым и пятым предложениями. Они говорят о том, что некие два объекта принадлежат общему классу: сыновей общих родителей, слов с фиксированным числом букв. Второе, третье и четвертое отношения имеют то общее, что выражают некоторый порядок объектов в системе.

В дальнейшем эта разница между отношениями того и другого типа будет четко определена. Первый и пятый пример — это отношения эквивалентности, определяющие разбиения множества объектов на классы подобных друг другу. Остальные три примера — это отношения порядка, устанавливающие относительное расположение объектов в системе.

Важно обратить внимание на тот факт, что во всех пяти примерах четко выделяются названия объектов (Иван, Киев и т.д.) и названия отношений (брат, старше, южнее и др.). Если вместо названия данного объекта подставить в предложение название другого объекта, то возможны следующие ситуации: 1) отношение опять будет выполнено; 2) отношение перестанет выполняться; 3) отношение потеряет смысл. Так, если в четвертое предложение вместо слова «железо» подставить слово «свинец», то суждение останется справедливым. Если в третье предложение вместо слова «Москва» подставить «Ашхабад», то оно перестанет быть верным. Если же в третье предложение вместо слова «Москва» подставить «железо», то суждение потеряет смысл. В отличие от первых четырех, в пятое предложение можно подставить любые слова, поскольку для любого слова имеет смысл говорить о числе букв. Здесь сама форма суждения ограничивает класс объектов — объектами отношения могут быть только слова.

Итак, говорить об отношении можно только тогда, когда мы умеем выделять множество объектов, на которых это отношение определено. Отношение может быть определено не только для пар объектов, но и для троек, четверок и т.д. Например, отношение «составлять экипаж лодки-восьмерки» выполняется для некоторых групп из восьми людей. Это отношение следует отличать от отношения «входить в экипаж одной и той же лодки-восьмерки», определенного для пар людей. Пример трехместных (или тернарных) отношений дают алгебраические операции. Отношение «образовывать произведение» имеет смысл для троек чисел и выполняется в том случае, когда x×y = z.

Мы будем рассматривать бинарные отношения, т.е. отношения, которые могут выполняться (или не выполняться) между двумя объектами из одного и того же множества. Поэтому в дальнейшем будем говорить об отношениях, имея в виду только бинарные отношения.

После выяснения содержательного смысла понятия отношения можно перейти к его точному определению, способам задания, свойствам и классификации отношений.

Отношением R на множестве W называется подмножество R множества WxW, т.е. R Í WxW. Содержательный смысл такого определения состоит в том, что задание подмножества R в множестве WxW определяет, какие пары находятся в отношении R. Это подчеркивается следующим соглашением об обозначениях. Если пара входит в R, т. е. Î R, то пишут xRy, что читается: «x находится в отношении R с у».

Подчеркнем, что отношение — это не просто множество соответствующих пар, а подмножество пар WxW при фиксированном множестве W. Множество W называется областью задания отношения. В тех случаях, где существенна область задания отношения, будем пользоваться для его обозначения парой .

Пусть W₁ — множество студентов группы, W₂ — множество студентов факультета, W₃ — множество студентов всего института. Естественно определяются три разных отношения: , , ; отношение R_i-множество таких пар , что «х знаком с у», но при i = 1 областью задания отношения является множество студентов одной, группы; при i = 2 — факультета, при i = 3 — института.

Таким образом, рассмотрение разных множеств приводит к разным отношениям.

2.1.2. Способы задания отношений

Для того чтобы задать отношение на множестве W, нужно указать все пары ÎWхW, которые содержатся в R, т.е. пары ÎW 2 , для которых выполняется отношение R.

Кроме непосредственного указания всех пар, для которых выполняется отношение R, существуют три основных способа задания отношения: задание отношения матрицей; задание отношения графом; задание отношения сечениями.

Остановимся подробнее на каждом из них, так как они необходимы далее для пояснения способов описания задач выбора и способов представления требуемой для их решения информации.

Задание матрицей. Рассмотрим пример. Пусть W — множество участников шахматного турнира. Будем говорить, что , для которых выполнено отношение «быть победителем», можно просто выписать турнирную таблицу, заменив половинки нулями (если участники х и у сыграли вничью, то никто из них не является победителем другого; в этом случае не выполнены оба соотношения: «х — победитель у» и «у — победитель х»). Приведем откорректированную таким образом таблицу турнира в Тилбурге в сентябре 1980 г. (табл. 1.1). Она иллюстрирует способ задания отношения на конечном множестве, который называется матричным.

А. Карпов

Л. Портиш

Я- Тимман

Г. Сосонко

Б. Спасский

М. Таль

В. Горт

Б. Ларсен

У. Андерсен

3. Рибли

Р. Хюбнер

Л. Кавалек

Задание графом. Поставим во взаимно однозначное соответствие элементам конечного множества W вершины графа x₁, . х_n (при некоторой нумерации). Проведем дугу от х_i к x_j тогда и только тогда, когда выполнено x_iRx_j (при i = j дуга (x_i, x_j) превращается в петлю при вершине x_i).

Изобразим в виде графа (рис. 2.1) турнирную табл. 2.1. Ясно, что петель в этом графе нет. Номера вершин соответствуют номерам участников в таблице.

Если задан произвольный граф G c n вершинами и выбрана нумерация на множестве W, то тем самым на W задается некоторое отношение R = R(G) такое, что x_iRx_j выполняется тогда и только тогда, когда в графе G есть дуга (x_i,x_j).

Граф является геометрическим представлением отношения, аналогично тому, как график является геометрическим представлением функции. Геометрический язык полезен, когда граф достаточно прост (либо у него мало вершин, либо он имеет простую структуру). Наоборот, изучать и описывать сложные графы с большим числом вершин часто удобнее в терминах отношений. В дальнейшем будем говорить о графе отношения R, обозначая его G(R).

Задание сечениями. Этот способ менее распространен, чем предыдущие. Однако, в отличие от них, он пригоден и для задания отношений на бесконечных множествах.

Рассмотрим отношение R на множестве Q.

Верхним сечением R + (x) называется множество элементов у Î W таких, что Î R:

R + (x)=<yÎWï ÎR>;

(2.1)

аналогично определяется нижнее сечение:

R — (x)=<yÎWï ÎR>;

(2.2)

Таким образом, множество R — (х) — это множество всех элементов yÎW, с которыми фиксированный элемент хÎW находится в отношении R. Множество R + (х) — это множество всех элементов yÎW, которые находятся в отношении R с фиксированным элементом хÎW.

Пусть W — множество участников шахматного турнира в Тилбурге. Запишем рядом с каждым элементом х_iÎW соответствующее верхнее сечение R + (x_i), т.е. множество номеров всех участников турнира, выигравших у х_i:

1-<8>,	5-<1,6>,	9-<1,5>,
2-0,	6-<2>,	10-<1,4,5>,
3-<1>,	7-<8>,	11-<1,3,8>,
4-0,	8-<2,3,5,10>,	12-<2,3,11>.

Приведенная запись полностью определяет отношение «у — победитель х».

В общем случае отношение R полностью задано, если для каждого xÎW задано множество R + (х) (или для каждого xÎW задано множество R — (x)).

Проиллюстрируем введенные способы задания отношений на четырех отношениях специального вида.

Отношение называется пустым (обозначается Æ), если оно не выполняется ни для одной пары ÎW 2 .

Для пустого отношения Æ справедливо:

1) матрица A(Æ) — такая, что a_ij(Æ) = 0 для всех i и j;

2) граф G (Æ) не имеет дуг;

3) R + (x) = R — (х) = Æ для любого xÎW . Отношение называется полным (обозначается U), если оно выполняется для всех пар ÎW 2 .

Для полного отношения U справедливо:

2) граф G (U) — такой, что дуги соединяют любую пару вершин;

Отношение называется диагональным или отношением равенства (обозначается Е), если оно выполняется для всех пар ÎW 2 , состоящих из совпадающих элементов: хЕу, если х и y — один и тот же элемент множества W.

Для диагонального отношения Е справедливо:

1) матрица А(Е) — такая, что

2) граф G(Е) — такой, что присутствуют только петли при всех вершинах, а других дуг нет;

Отношение называется антидиагональным (обозначается ), если оно выполняется для всех пар ÎW 2 , состоящих из несовпадающих элементов.

Для антидиагонального отношения справедливо:

1) матрица А ( ) — такая, что

2) граф G ( ) — такой, что присутствуют все дуги при i¹j (отсутствуют только петли);

Операции над отношениями

Рассмотрим основные операции над отношениями. Поскольку любое отношение R есть подмножество множеств; пар Ω 2 , то для отношений можно определить все те операции которые определены для подмножеств фиксированного множества: пересечение, объединение, дополнение и т.д.

1. Объединением R₁ÈR₂ отношений R₁ и R₂ называется бинарное отношение, которое включает все пары (x,y), содержащиеся в R₁ или R₂.

2. Пересечением R₁ÇR₂ называется бинарное отношение, которое содержит только общие для R₁ и R₂ пары (x,y). Если R₁ и R₂ не имеют общих пар, то говорят, что их пересечение пусто и записывают R₁ÇR₂ = Æ.

3. Разностью R₁\R₂ отношений R₁ и R₂ называют бинарное отношение, составленное из тех пар (x,y), которые содержатся в R₁ и не содержатся в R₂.

5. Дополнением 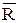к отношению R называют бинарное отношение, содержащее те и только те пары (x,y) из W, которые не входят в R, т.е. = W\R. ясно, что пересечение ÇR = Æ.

6. Композицией (произведением) R₁ ° R₂ отношений R₁ и R₂ называют бинарное отношение, которое содержит пару (x,y) тогда и только тогда, когда существует zÎW, такое, что (x, z) Î R₁, (z, y) Î R₂.

7. Обратным отношением R -1 к отношению R называют бинарное отношение, содержащее пару (x,y) в том и только в том случае, когда (x,y)ÎR, т.е. xR -1 y Û yRx.

Функции выбора

Ранее уже были рассмотрены математические конструкции для описания результатов выбора из конечного множества. Наиболее общая из таких конструкций функция выбора. Менее общей конструкцией является бинарное отношение. Между названными конструкциями существует взаимосвязь, которая позволяет описать результаты произвольных выборов из конечного множества любой из этих конструкций. Для выявления такой взаимосвязи потребуется понятие декомпозиции (разложения) функции выбора.

Общими декомпозициями называются такие конструкции, которые применимы к любой функции выбора, а частными декомпозициями — такие, которые применимы к функциям выбора только из некоторого класса.

Понятие функции выбора

Подмножество возможных в некоторой ситуации решений, каждое из которых является «хорошим» решением для соответствующей задачи называется выбором.

Функция выбора – это многозначное отображение, определяющее зависимость выбора от предъявления.

Предъявление – ситуация описанная в терминах определяемых его возможных решений.

Примером функции выбора являются действия опытного командира в условиях быстроменяющейся обстановки.

Функция выбора, записанная для достаточно большого количества ситуаций определенного класса, может служить основанием для автоматизации процесса выбора решений в соответствующем классе задач.

Обозначим через G множество возможных решений для всех задач класса, через X Í G множество возможных решений для конкретной задачи X, а через С(X) Í X – множество «хороших» решений задачи X. Отображение

представляет собой функцию выбора.

Более просто функция выбора определят понятия: «рациональный», справедливый, выбор в ситуации X, принадлежащей заданному классу.

Другое фундаментальное понятие ТПР – механизм выбора – указывает, как произвести выбор, рациональный с точки зрения заданной функции выбора. Механизм выбора обычно реализуется в виде алгоритма или организационной системы помогающих в заданной ситуации обеспечить выбор решения.

Различают частные и полные функции выбора. Первые определяют рациональное решение не для всех ситуаций изучаемого класса и отображают накопленный опыт и знания. Полные функции выбора определяют расширенные множества ситуаций на которых определен рациональный выбор и проводится за счет дополнительного экспериментирования.

Функция выбора непосредственно приводит в соответствие каждой ситуации выбора «рациональное» решение независимо от механизма выбора и от условий, определяющих «рациональный» выбор.

Формальное определение функции выбора:

Пусть множество G представляет собой множество альтернатив, а b — семейство некоторых подмножеств множества G. Пара (G,b) называется обстановкой, а элемент хсемейства b- предъявлением.

Выбор в обстановке (G,b) соответствует предъявлению хÎbего подмножество Y = C(X) Í X – множество альтернативхÎb отобранных ЛПР в предъявлении х.

b Ì 2 G – для частной функции выбора,

b = 2 G – для полной функции выбора.

Функция выбора может быть задана таблицей, набором свойств (аксиом), механизмом выбора или гибридным путем.

Источник