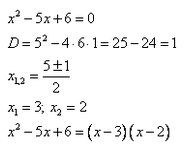Способы решения неравенства егэ

Задание 14. Неравенства — профильный ЕГЭ по математике

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства

1. Решите неравенство:

Решим неравенство относительно t методом интервалов:

Вернемся к переменной x:

Показательные неравенства

2. Решите неравенство

Сделаем замену Получим:

Умножим неравенство на

Дискриминант квадратного уравнения

Значит, корни этого уравнения:

Разложим квадратный трехчлен на множители.

. Вернемся к переменной x.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,

3. Решите неравенство

Сделаем замену Получим:

Вернемся к переменной

Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х?

Оценим Для этого рассмотрим функцию

Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом

Мы получили, что

Тогда , и это значит, что Значение не достигается ни при каких х.

Логарифмические неравенства

4. Решите неравенство

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство:

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,

Согласно методу замены множителя, выражение заменим на

Решить ее легко.

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ.

Источник

Решение неравенств

Решите неравенство \[x+10

Перенесем слагаемые в левую часть: \[-3x^2+x+10 Разложим на множители выражение \(-3x^2+x+10\) : \[-3x^2+x+10=0 \quad \Rightarrow \quad x_1=2\quad\text<и>\quad x_2=-\dfrac53\] Следовательно, \(-3x^2+x+10=-3(x-2)\left(x-\frac53\right)=-(x-2)(3x+5)\) .
Тогда неравенство примет вид \[-(x-2)(3x+5) 0\] Решим его методом интервалов:

Таким образом, подходят \(x\in \left(-\infty;-\frac53\right)\cup(2;+\infty)\) .

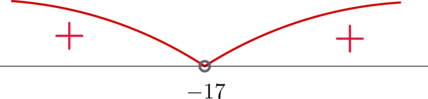
Решите неравенство \[x^2+34x+289>0\]

Заметим, что по формуле квадрата суммы \(x^2+34x+289=(x+17)^2\) , следовательно, неравенство принимает вид: \[(x+17)^2>0\] Решим его методом интервалов:

Таким образом, нам подходят \(x\in(-\infty;-17)\cup(-17;+\infty)\) .

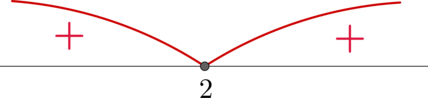
Решите неравенство \[x^2-4x+4\leqslant 0\]

Заметим, что по формуле квадрата разности \(x^2-4x+4=(x-2)^2\) , следовательно, неравенство принимает вид: \[(x-2)^2\leqslant 0\] Решим его методом интервалов:

Таким образом, нам подходят \(x\in\<2\>\) .

Решите неравенство \[x^2+3x+3\geqslant 0\]

Разложим на множители выражение \(x^2+3x+3\) , для этого решим уравнение \(x^2+3x+3=0\) . Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех \(x\) . Проверить его знак можно, подставив вместо \(x\) любое число, например, \(x=0\) : получим \(3\) , следовательно, выражение всегда \(>0\) .

Таким образом, нам подходят \(x\in \mathbb\) .

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения \[(x — 1)(x + 2) = 0\] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: \[x = 1,\qquad\qquad x = -2\]

2) Найдём нули знаменателя: \[(x — 3)(x + 4) = 0\qquad\Leftrightarrow\qquad \left[ \begin x = 3\\ x = -4 \end \right.\]

По методу интервалов:

откуда \[x\in(-4; -2]\cup[1; 3)\,.\] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения \[(x + 1)(x — 2) = 0\] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: \[x = -1,\qquad\qquad x = 2\]

2) Найдём нули знаменателя: \[(x + 3)(x^2 + 4) = 0\] так как \(x^2\geqslant 0\) , то \(x^2 + 4\geqslant 4\) , следовательно, нули знаменателя: \[x = -3\]

По методу интервалов:

откуда \[x\in(-\infty; -3)\cup[-1; 2]\,.\] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Источник

Метод интервалов, решение неравенств

О чем эта статья:

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
3. D

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.

Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.

Когда квадратный трехчлен корней не имеет (D

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.

Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

Отобразим эти данные на чертеже:

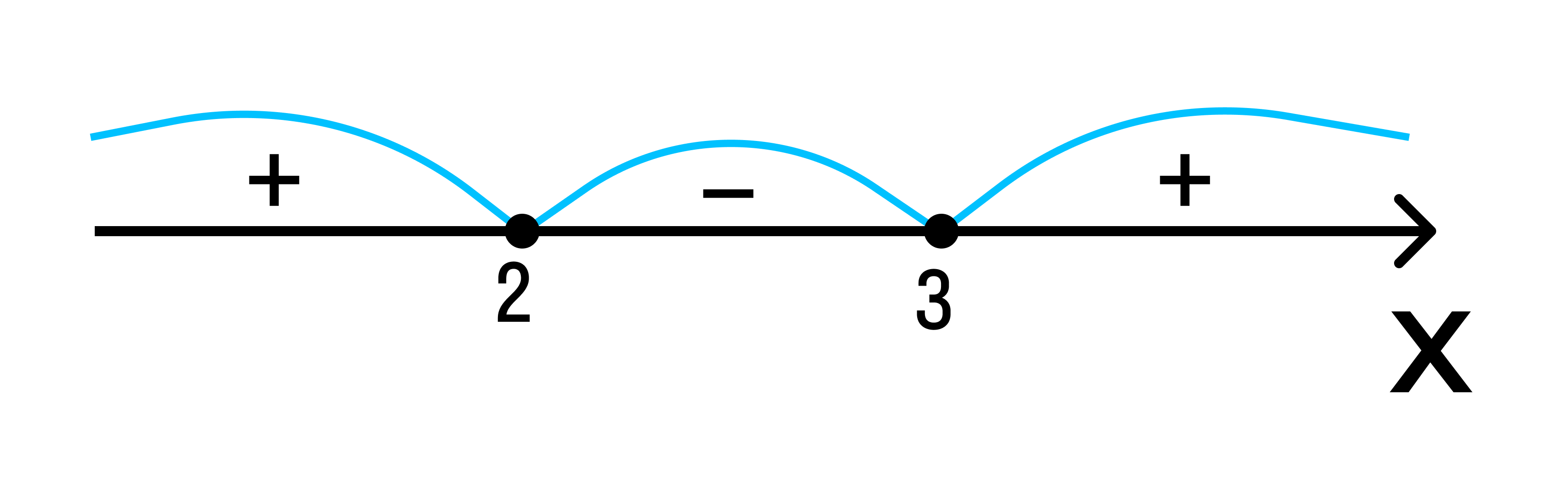
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• (25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Методы решения неравенств при подготовке к ЕГЭ

Методы решения неравенств при подготовке к ЕГЭ

Решить неравенство значит найти множество всех решений неравенства или доказать, что оно решений не имеет. При решении неравенств мы пользуемся равносильными преобразованиями в рамках ОДЗ. С помощью равносильных преобразований мы сводим неравенство к рациональному. Основным методом решения рациональных неравенств является метод интервалов.

Рассмотрим решение задания 13 одного из вариантов ЕГЭ нашего региона.

Задание одного из вариантов было другого типа

Такие неравенства эффективнее решать методом рациональных замен.

Монотонность – ключ к замене.

Выражение при ( — возрастающая функция) имеет тот же знак, что и и противоположный, если ( — убывающая функция)

Оба варианта можно объединить в один , имеющий тот же знак, что и исходное выражение .

Решить неравенство :

Решение. Заменим неравенство равносильной системой, где учитывается область определения логарифмической функции.

,

Решить неравенство :

Решение.

Выражение и имеют один знак.

Заменим исходное неравенство равносильной системой, где учитывается область определения логарифмической функции.

.

Ответ:

Полезная таблица замены показательных и логарифмических неравенств на равносильные

Источник

Читайте также:  Эссе способы разрешения конфликтов как инструмент эффективности управления персоналом