Способы решения неравенств со степенями

Основные положения и примеры решения простейших показательных неравенств.

Показательные неравенства содержат переменную в показателе степени. В случае, если вам встретилось неравенство, в котором переменная не только в показателе, но и в основании степени, попробуйте применить метод рационализации, о котором несколько слов в конце статьи. Если же неизвестная величина только в основании степени, а показатели фиксированы, то это неравенство относится к рациональным и содержит не показательные, а степенные функции.

Чтобы решать показательные неравенства нужно вспомнить, что мы знаем о показательной функции.

Область определения показательной функции D = R, то есть всё множество действительных чисел. Иначе записывают \(x\in(-\infty; +\infty)\). Область значений функции \(E = (0; +\infty)\), т.е. результат может принимать только положительные значения.
Функция монотонна: одному значению аргумента соответствует только одно значение функции.

При a > 1 функция возрастающая,

Поэтому для решения простейших показательных неравенств достаточно свести обе части неравенства к степени с одинаковым основанием (выравнять основания) и затем сравнить показатели степени. Т.е. как бы сравнивать функцию с самой собой при разных значениях её аргумента. При этом, если основание степени больше единицы, то знак неравенства для показателей будет таким же, как знак исходного неравенства, что характерно для возрастающих функций – большему значению аргумента соответствует большее значение функции. Если основание степени меньше единицы, то знак неравенства для показателей будет обратным по отношению к знаку исходного неравенства, что характерно для убывающих функций – большему значению аргумента соответствует меньшее значение функции.

Пример 1.

Решить неравенство \[\left(\frac<1><3>\right)^ > \frac<1><9>\]

Решение.

Представим одну девятую как одну третью в квадрате, тогда \[\left(\frac<1><3>\right)^ > \left(\frac<1><3>\right)^2\] Основанием степени в обоих частях неравенства является \(\dfrac<1><3>\). Одна третья меньше единицы, показательная функция является убывающей, большему значению аргумента соответствует меньшее значение функции, следовательно при переходе к сравнению показателей знак неравенства развернётся. Получим \[x-8 5.\]

Решение.

На первый взгляд числа 3 и 5 таковы, что выражения не могут быть сведены к одному основанию в какой-либо степени. На этот случай у нас определена обратная к показательной логарифмическая функция. Мы говорим, что обе части неравенства нужно прологарифмировать по одному основанию. Однако, на мой взгляд, именно для решения неравенств лучше всего использовать следующее свойство логарифма, вытекающее из его определения \(b = a^<\log_ab>\). Здесь основания степени и логарифма совпадают, поэтому при вычислении логарифма как бы «сокращаются», значит «восстановить» можно любые допустимые значения, нужные для решения конкретного неравенства. Этим приёмом мы и будем пользоваться в дальнейшем, чтобы разбираться со знаком неравенства по той же схеме, что и в предыдущих двух примерах.

Итак, представим правую часть неравенства следующим образом \(5 = 3^<\log_35>,\) тогда \[ 3^ > 3^ <\log_35>\\ x+5 > \log_3 <5>\\ x > -5 + \log_3<5>.\] Можно вычислить примерное значение \(-5 + \log_3<5>\) с помощью калькулятора, оно составляет ≈ −3,535. Но точный ответ неравенства, если он получается с иррациональными числами, так и записывают через логарифм.

Ответ: \(x \in [-5 + \log_3<5>;\; +\infty). \)

Итак, при решении простейших неравенств следует выравнять основания степеней, а затем их отбросить и перейти к сравнению показателей. При этом очень важно следить за отношением основания степени к единице. Если \(a > 1\) при переходе к сранению показателей знак неравенства сохраняется, если \(a x 2 − 8x 7

Решение.

Заметим, что 0,2 = \(\dfrac<1><5>\) и уравняем основания левой и правой части. \[\left(\frac<1><5>\right)^ -7; \\x^2 — 8x + 7 > 0.\] Корни квадратного трёхчлена те же, ветви параболы направлены вверх, но так как теперь требуется, чтобы они находились выше оси абсцисс, то интервалы выполнения неравенства будут теми же: \((-\infty;1)\) и \((7; +\infty;)\).

Ответ: x ∈ (−∞;1) ∪ (7;+∞).

Введение вспомогательной переменной

Решение.

Преобразуем левую часть, используя свойства степеней. \[3^4\cdot3^ <-3x>— 35\cdot\frac<1^<2 - 3x>><3^<2 - 3x>> + 6 \ge 0; \\ \frac<3^4><3^<3x>> — 35\cdot\frac<1><3^2\cdot3^<- 3x>> + 6 \ge 0; \\ \frac<3^4><3^<3x>> — 35\cdot\frac<3^<3x>> <3^2>+ 6 \ge 0. \]

В последнем неравенстве неизвестная величина встречается дважды и только в показателе степени тройки, причем оба раза в одинаковой форме, поэтому можно продолжить решение методом введения вспомогательной переменной.

Пусть \(y = 3^<3x>\). Причём по определению показательной функции мы должны рассматривать только положительные значения y. Тогда неравенство принимает вид \[\frac<3^4> — 35\cdot\frac <3^2>+ 6 \ge 0. \] Известные степени тройки вычислим и всё выражение приведём к общему знаменателю. \[\frac<81> — 35\cdot\frac <9>+ 6 \ge 0; \\ \frac<81\cdot9 - 35\cdot y^2 + 6\cdot9\cdot y > <9y>\ge 0;\\ \frac<729 - 35y^2 + 54y> <9y>\ge 0. \] Учитывая, что знаменатель этой дроби может быть лишь положительным, так как \(y > 0\), то остаётся решить квадратное неравенство \[729 — 35y^2 + 54y \ge 0.\] Проделайте это самостоятельно. Должен получиться следующий результат \[-\frac<27> <7>\le y \le \frac<27><5>.\] Из этого ответа берём только положительную часть \(0 1), окончательно получаем \[3x \le \log_3<\frac<27><5>> \\ x \le \frac<1><3>\log_3\frac<27><5>. \]

Ответ: \(x \in (-\infty; \;\dfrac<1><3>\log_3\dfrac<27><5>) \).

Замечание: При желании этот ответ можно преобразовать, используя формулу для логарифма дроби. \[\frac<1><3>\log_3\frac<27> <5>= \frac<1><3>(\log_327 — \log_35) = \frac<1><3>(3 — \log_35) = 1 — \frac<1><3>\log_35. \]

Разложение на множители

Решение.

Здесь в правой и левой частях неравенства разные основания и привести выражение к одному основанию, пользуясь только свойствами степени не получится, потому что свойства относятся к операциям умножения, деления и возведения в степень, а мы имеем с обоих сторон суммы показательных функций. В этом случае надо стараться разложить выражения на множители. Здесь это можно будет сделать вынесением общего множителя за скобки, а вообще для решения подобных неравенств очень рекомендую повторить различные способы разложения на множители, особенно формулы сокращенного умножения. \[ 3^ + 3^ + 3^ \le 2^x + 2^ + 2^; \\ 3^ + 3^\cdot3^1 + 3^\cdot3^2 \le 2^x + 2^\cdot2^ <-1>+ 2^\cdot2^<-2>; \\ 3^ + 3^\cdot3 + 3^\cdot9 \le 2^x + 2^\cdot\frac<1> <2>+ 2^\cdot\frac<1><4>; \\ 3^(1 + 3 + 9) \le 2^x(1 + \frac<1> <2>+ \frac<1><4>); \\ 3^\cdot13 \le 2^x\cdot\frac<7><4>.\] Чтобы все величины, содержащие переменную х, оказались в левой части неравенства, а все числа – в правой, разделим обе его части на \(2^x\cdot13\) и проведём необходимые сокращения дробей. Это не приведёт к изменению знака неравенства, так как нам заведомо известно, что делим на положительное выражение. \[\frac<3^x\cdot13><2^x\cdot13>\le\frac<2^x\cdot7><4\cdot2^x\cdot13>;\\ \frac<3^x> <2^x>\le \frac<7><4\cdot13>;\\ \left(\frac<3><2>\right)^x \le \frac<7><52>.\] Пользуясь определением логарифма выравниваем основания \[\left(\frac<3><2>\right)^x \le \left(\frac<3><2>\right)^ <\log_<\frac<3><2>><\frac<7><52>>>.\] Учитывая, что \(\dfrac<3> <2>> 1\), получим \[x \le \log_<\frac<3><2>><\frac<7><52>>.\]

О методе рационализации.

Метод рационализации для показательных неравенств сводится к следующему:

неравенство вида \[(h(x))^<\large>\geqslant (h(x))^<\large>\] равносильно системе \[\begin (h(x)-1)(f(x)-g(x))\geqslant 0\\[1ex] h(x)>0 \end\] Например, чтобы получить решение показательного неравенства \(3^ 0 \end\]

Очевидно, что в случае числового основания степени это решение не является более простым и более понятным, чем решение предыдущих примеров. Метод рационализации существенно сокращает объём рассуждений и выкладок, когда в основании степени также как и в её показателе находятся неизвестные переменные величины. И хотя такие неравенства относятся к более сложным типам, чем те, которые бывают на ЕГЭ даже профильного уровня, рассмотрим пример.

Решение.

Обратите внимание – для решения показательных неравенств методом рационализации тоже нужно выравнивать основания степеней или, как в этом примере, иметь их одинаковыми по условию задачи.

Заменяем неравенство на равносильную систему \[\begin \left(\dfrac-1\right)\Large(\normalsize(x-1)-(2x)\Large)\normalsize\le 0;\\[1ex] \dfrac>0 \end\] Далее решаем каждое неравенство системы методом интервалов.

\[\left(\frac-1\right)\Large(\normalsize(x-1)-(2x)\Large)\normalsize\le 0;\\ \left(\frac\right)(x-1-2x)\le 0;\\ \left(\frac<- x^2+x+1><(x-1)(x+1)>\right)(-x-1)\le 0;\\ \frac<(x^2-x-1)(x+1)><(x-1)(x+1)>\le 0.\] Чтобы разложить квадратный трёхчлен на множители нужно решить уравнение \(x^2-x-1=0\).
Решив, получим корни \(\dfrac<1-\sqrt<5>> <2>\approx -0,62\) и \(\dfrac<1+\sqrt<5>> <2>\approx 1,62\).

Обратите внимание – дробь с неизвестными в знаменателе можно сокращать только после того, как записали ОДЗ. Мы ОДЗ не записывали, поэтому сокращать не будем. Тот факт, что на 0 делить нельзя, отметим непосредственно на числовой оси.

Общее решение системы

Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания? Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Источник

Решение показательных неравенств: основные способы

Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое. И что научиться их решать — чуть ли не великое искусство, постичь которое способны лишь Избранные.

Полная брехня! Показательные неравенства — это просто. И решаются они всегда просто. Ну, почти всегда.:)

Сегодня мы разберём эту тему вдоль и поперёк. Этот урок будет очень полезен тем, кто только начинает разбираться в данном разделе школьной математики. Начнём с простых задач и будем двигаться к более сложным вопросам. Никакой жести сегодня не будет, но того, что вы сейчас прочитаете, будет достаточно, чтобы решить большинство неравенств на всяких контрольных и самостоятельных работах. И на этом вашем ЕГЭ тоже.

Как всегда, начнём с определения. — это любое неравенство, содержащее в себе показательную функцию. Другими словами, его всегда можно свести к неравенству вида

Где в роли $b$ может быть обычное число, а может быть и что-нибудь пожёстче. Примеры? Да пожалуйста:

Конечно, в некоторых случаях неравенство может выглядеть более сурово. Вот, например:

Решение простейших показательных неравенств

Рассмотрим что-нибудь совсем простое. Например, вот это:

Очевидно, что число справа можно переписать в виде степени двойки: $4=<<2>^<2>>$. Таким образом, исходное неравенство перепишется в очень удобной форме:

И вот уже руки чешутся «зачеркнуть» двойки, стоящие в основаниях степеней, дабы получить ответ $x \gt 2$. Но перед тем как что там зачёркивать, давайте вспомним степени двойки:

Как видим, чем большее число стоит в показателе степени, тем больше получается число на выходе. «Спасибо, кэп!» — воскликнет кто-нибудь из учеников. Разве бывает по-другому? К сожалению, бывает. Например:

Тут тоже всё логично: чем больше степень, тем больше раз число 0,5 умножается само на себя (т.е. делится пополам). Таким образом, полученная последовательность чисел убывает, а разница между первой и второй последовательностью состоит лишь в основании:

Суммируя эти факты, мы получаем самое главное утверждение, на котором и основано всё решение показательных неравенств:

Другими словами, если основание больше единицы, его можно просто убрать — знак неравенства при этом не поменяется. А если основание меньше единицы, то его тоже можно убрать, но при этом придётся поменять и знак неравенства.

Обратите внимание: мы не рассмотрели варианты $a=1$ и $a\le 0$. Потому что в этих случаях возникает неопределённость. Допустим, как решить неравенство вида $<<1>^> \gt 3$? Единица в любой степени снова даст единицу — мы никогда не получим тройку или больше. Т.е. решений нет.

С отрицательными основаниями всё ещё интереснее. Рассмотрим для примера вот такое неравенство:

На первый взгляд, всё просто:

Правильно? А вот и нет! Достаточно подставить вместо $x$ парочку чётных и парочку нечётных чисел, чтобы убедиться что решение неверно. Взгляните:

Как видите, знаки чередуются. А ведь есть ещё дробные степени и прочая жесть. Как, например, прикажете считать $<<\left( -2 \right)>^<\sqrt<7>>>$ (минус двойка в степени корень из семи)? Да никак!

Поэтому для определённости полагают, что во всех показательных неравенствах (и уравнениях, кстати, тоже) $1\ne a \gt 0$. И тогда всё решается очень просто:

В общем, ещё раз запомните главное правило: если основание в показательном уравнении больше единицы, его можно просто убрать; а если основание меньше единицы, его тоже можно убрать, но при этом поменяется знак неравенства.

Примеры решения

Итак, рассмотрим несколько простых показательных неравенств:

Что здесь можно сделать? Ну, слева у нас и так стоит показательное выражение — ничего менять не надо. А вот справа стоит какая-то хрень: дробь, да ещё и в знаменателе корень!

Однако вспомним правила работы с дробями и степенями:

Что это значит? Во-первых, мы легко можем избавиться от дроби, превратив её в степень с отрицательным показателем. А во-вторых, поскольку в знаменателе стоит корень, было бы неплохо превратить и его в степень — на этот раз с дробным показателем.

Применим эти действия последовательно к правой части неравенства и посмотрим, что получится:

Не забываем, что при возведении степени в степень показатели этих степеней складываются. И вообще, при работе с показательными уравнениями и неравенствами совершенно необходимо знать хотя бы простейшие правила работы со степенями:

Собственно, последнее правило мы только что и применили. Поэтому наше исходное неравенство перепишется следующим образом:

Теперь избавляемся от двойки в основании. Поскольку 2 > 1, знак неравенства останется прежним:

Вот и всё решение! Основная сложность — вовсе не в показательной функции, а в грамотном преобразовании исходного выражения: нужно аккуратно и максимально быстро привести его к простейшему виду.

Рассмотрим второе неравенство:

Так, так. Тут нас поджидают десятичные дроби. Как я уже много раз говорил, в любых выражениях со степенями следует избавляться от десятичных дробей — зачастую только так можно увидеть быстрое и простое решение. Вот и мы избавимся:

Перед нами вновь простейшее неравенство, да ещё и с основанием 1/10, т.е. меньшим единицы. Что ж, убираем основания, попутно меняя знак с «меньше» на «больше», и получаем:

Получили окончательный ответ: $x\in \left( -\infty ;-1 \right)$. Обратите внимание: ответом является именно множество, а ни в коем случае не конструкция вида $x \lt -1$. Потому что формально такая конструкция — это вовсе не множество, а неравенство относительно переменной $x$. Да, оно очень простое, но это не ответ!

Важное замечание. Данное неравенство можно было решить и по-другому — путём приведения обеих частей к степени с основанием, большим единицы. Взгляните:

После такого преобразования мы вновь получим показательное неравенство, но с основанием 10 > 1. А это значит, что можно просто зачеркнуть десятку — знак неравенства при этом не поменяется. Получим:

Как видите, ответ получился точь-в-точь такой же. При этом мы избавили себя от необходимости менять знак и вообще помнить какие-то там правила.:)

Идём далее. Рассмотрим чуть более сложное неравенство — в нём в показателе появляется квадратичная функция:

Однако пусть вас это не пугает. Чтобы ни находилось в показателях, технология решения самого неравенства остаётся прежней. Поэтому заметим для начала, что 16 = 2 4 . Перепишем исходное неравенство с учётом этого факта:

Ура! Мы получили обычное квадратное неравенство! Знак нигде не менялся, поскольку в основании стоит двойка — число, большее единицы.

Далее можно воспользоваться теоремой Виета, либо просто решить уравнение $<^<2>>-7x+10=0$ через дискриминант. В любом случае корни будут $<_<1>>=2$ и $<_<2>>=5$. Отметим их на числовой прямой:

Нули функции на числовой прямой

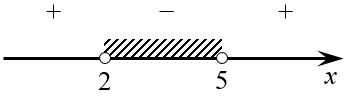
Расставляем знаки функции $f\left( x \right)=<^<2>>-7x+10$ — очевидно, её графиком будет парабола ветвями вверх, поэтому по бокам будут «плюсы». Нас интересует та область, где функция меньше нуля, т.е. $x\in \left( 2;5 \right)$ — это и есть ответ к исходной задаче.

Наконец, рассмотрим ещё одно неравенство:

Опять видим показательную функцию с десятичной дробью в основании. Переводим эту дробь в обыкновенную:

В данном случае мы воспользовались приведённым ранее замечанием — свели основание к числу 5 > 1, чтобы упростить себе дальнейшее решение. Точно так же поступим и с правой частью:

Перепишем исходное неравенство с учётом обоих преобразований:

Основания с обеих сторон одинаковы и превосходят единицу. Никаких других слагаемых справа и слева нет, поэтому просто «зачёркиваем» пятёрки и получаем совсем простое выражение:

Вот тут надо быть аккуратнее. Многие ученики любят просто извлечь квадратный корень их обеих частей неравенства и записать что-нибудь в духе $x\le 1\Rightarrow x\in \left( -\infty ;-1 \right]$. Делать этого ни в коем случае нельзя, поскольку корень из точного квадрата — это модуль, а ни в коем случае не исходная переменная:

Однако работать с модулями — не самое приятное занятие, правда? Вот и мы не будем работать. А вместо этого просто перенесём все слагаемые влево и решим обычное неравенство методом интервалов:

Вновь отмечаем полученные точки на числовой прямой и смотрим знаки:

Обратите внимание: точки закрашены

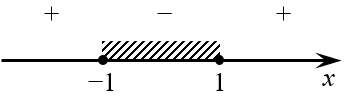
Поскольку мы решали нестрогое неравенство, все точки на графике закрашены. Поэтому ответ будет такой: $x\in \left[ -1;1 \right]$ — не интервал, а именно отрезок.

В целом хотел бы заметить, что ничего сложного в показательных неравенствах нет. Смысл всех преобразований, которые мы сегодня выполняли, сводится к простому алгоритму:

По сути, это универсальный алгоритм решения всех таких неравенств. А всё, что вам ещё будут рассказывать по этой теме — лишь конкретные приёмы и хитрости, позволяющие упростить и ускорить преобразования. Вот об одном из таких приёмов мы сейчас и поговорим.:)

Метод рационализации

Рассмотрим ещё одну партию неравенств:

Ну и что в них такого особенного? Они же лёгкие. Хотя, стоп! Число π возводится в какую-то степень? Что за бред?

А как возвести в степень число $2\sqrt<3>-3$? Или $3-2\sqrt<2>$? Составители задач, очевидно, перепили «Боярышника» перед тем, как сесть за работу.:)

Получается, что все эти «устрашающие» неравенства ничем не отличаются решаются от простых, рассмотренных выше? И решаются точно так же? Да, совершенно верно. Однако на их примере я хотел бы рассмотреть один приём, который здорово экономит время на самостоятельных работах и экзаменах. Речь пойдёт о методе рационализации. Итак, внимание:

Вот и весь метод.:) А вы думали, что будет какая-нибудь очередная дичь? Ничего подобного! Но этот простой факт, записанный буквально в одну строчку, значительно упростит нам работу. Взгляните:

Вот и нет больше показательных функций! И не надо помнить: меняется знак или нет. Но возникает новая проблема: что делать с грёбаным множителем \[\left( \text< >\!\!\pi\!\!\text< >-1 \right)\]? Мы ведь не знаем, чему равно точное значение числа π. Впрочем, капитан очевидность как бы намекает:

\[\text< >\!\!\pi\!\!\text< >\approx 3,14. \gt 3\Rightarrow \text< >\!\!\pi\!\!\text< >-1 \gt 3-1=2\]

В общем, точное значение π нас особо-то и не колышет — нам лишь важно понимать, что в любом случае $\text< >\!\!\pi\!\!\text< >-1 \gt 2$, т.е. это положительная константа, и мы можем разделить на неё обе части неравенства:

Как видите, в определённый момент пришлось разделить на минус единицу — при этом знак неравенства поменялся. В конце я разложил квадратный трёхчлен по теореме Виета — очевидно, что корни равны $<_<1>>=5$ и $<_<2>>=-1$. Дальше всё решается классическим методом интервалов:

Решаем неравенство методом интервалов

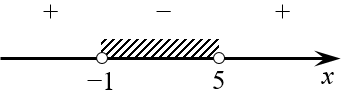
Все точки выколоты, поскольку исходное неравенство строгое. Нас интересует область с отрицательными значениями, поэтому ответ: $x\in \left( -1;5 \right)$. Вот и всё решение.:)

Перейдём к следующей задаче:

Тут вообще всё просто, потому что справа стоит единица. А мы помним, что единица — это любое число в нулевой степени. Даже если этим числом является иррациональное выражение, стоящее в основании слева:

Что ж, выполняем рационализацию:

Осталось лишь разобраться со знаками. Множитель $2\left( \sqrt<3>-2 \right)$ не содержит переменной $x$ — это просто константа, и нам необходимо выяснить её знак. Для этого заметим следующее:

\[\begin \sqrt <3>\lt \sqrt<4>=2 \\ \Downarrow \\ 2\left( \sqrt<3>-2 \right) \lt 2\cdot \left( 2-2 \right)=0 \\\end\]

Получается, что второй множитель — не просто константа, а отрицательная константа! И при делении на неё знак исходного неравенства поменяется на противоположный:

Теперь всё становится совсем очевидно. Корни квадратного трёхчлена, стоящего справа: $<_<1>>=0$ и $<_<2>>=2$. Отмечаем их на числовой прямой и смотрим знаки функции $f\left( x \right)=x\left( x-2 \right)$:

Случай, когда нас интересуют боковые интервалы

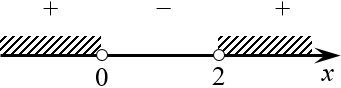
Нас интересуют интервалы, отмеченные знаком «плюс». Осталось лишь записать ответ:

\[x\in \left( -\infty ;0 \right)\bigcup \left( 2;+\infty \right)\]

Переходим к следующему примеру:

Ну, тут совсем всё очевидно: в основаниях стоят степени одного и того же числа. Поэтому я распишу всё кратко:

Далее «причёсываем» выражения с обеих частей неравенства и применяем метод рационализации:

Как видите, в процессе преобразований пришлось умножать на отрицательное число, поэтому поменялся знак неравенства. В самом конце я вновь применил теорему Виета для разложения на множители квадратного трёхчлена. В итоге ответ будет следующий: $x\in \left( -8;4 \right)$ — желающие могут убедиться в этом, нарисовав числовую прямую, отметив точки и посчитав знаки. А мы тем временем перейдём к последнему неравенству из нашего «комплекта»:

Как видим, в основании снова стоит иррациональное число, а справа снова стоит единица. Поэтому перепишем наше показательное неравенство следующим образом:

Однако совершенно очевидно, что $1-\sqrt <2>\lt 0$, поскольку $\sqrt<2>\approx 1,4. \gt 1$. Поэтому второй множитель — вновь отрицательная константа, на которую можно разделить обе части неравенства:

\[\begin \left( 3x-<^<2>>-0 \right)\cdot 2\left( 1-\sqrt <2>\right) \lt 0 \\ \Downarrow \\\end\]

Далее всё просто: находим корни, отмечаем их на числовой прямой, смотрим знаки. Ответ будет следующим: $x\in \left( 0;3 \right)$.

Переход к другому основанию

Отдельной проблемой при решении показательных неравенств является поиск «правильного» основания. К сожалению, далеко не всегда при первом взгляде на задание очевидно, что брать за основание, а что делать степенью этого основания.

Но не переживайте: здесь нет никакой магии и «секретных» технологий. В математике любой навык, который нельзя алгоритмизировать, можно легко выработать с помощью практики. Но для этого придётся решать задачи разного уровня сложности. Например, вот такие:

Сложно? Страшно? Да это же проще, чем цыплёнка об асфальт! Давайте попробуем. Первое неравенство:

Ну, я думают, тут и ежу всё понятно:

Переписываем исходное неравенство, сводя всё к основанию «два»:

Да, да, вы всё правильно поняли: я только что применил метод рационализации, описанный выше. Теперь нужно работать аккуратно: у нас получилось дробно-рациональное неравенство (это такое, у которого в знаменателе стоит переменная), поэтому прежде чем что-то приравнивать к нулю, необходимо привести всё к общему знаменателю и избавиться от множителя-константы.

Теперь используем стандартный метод интервалов. Нули числителя: $x=\pm 4$. Знаменатель обращается в ноль только при $x=0$. Итого три точки, которые надо отметить на числовой прямой (все точки выколоты, т.к. знак неравенства строгий). Получим:

Более сложный случай: три корня

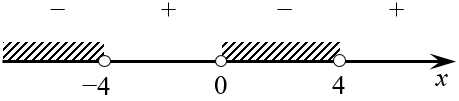
Как нетрудно догадаться, штриховкой отмечены те интервалы, на которых выражение слева принимает отрицательные значения. Поэтому в окончательный ответ пойдут сразу два интервала:

\[x\in \left( -\infty ;-4 \right)\bigcup \left( 0;4 \right)\]

Концы интервалов не входят в ответ, поскольку исходное неравенство было строгим. Никаких дополнительных проверок этого ответа не требуется. В этом плане показательные неравенства намного проще логарифмических: никаких ОДЗ, никаких ограничений и т.д.

Переходим к следующей задаче:

Здесь тоже никаких проблем, поскольку мы уже знаем, что $\frac<1><3>=<<3>^<-1>>$, поэтому всё неравенство можно переписать так:

Обратите внимание: в третьей строчке я решил не мелочиться и сразу разделить всё на (−2). Минул ушёл в первую скобку (теперь там везде плюсы), а двойка сократилась с множителем-константой. Именно так и стоит поступать при оформлении реальных выкладок на самостоятельных и контрольных работах — не надо расписывать прям каждое действие и преобразование.

Далее в дело вступает знакомый нам метод интервалов. Нули числителя: а их нет. Потому что дискриминант будет отрицательный. В свою очередь знаменатель обнуляется лишь при $x=0$ — как и в прошлый раз. Ну и понятно, что справа от $x=0$ дробь будет принимать положительные значения, а слева — отрицательные. Поскольку нас интересуют именно отрицательные значения, то окончательный ответ: $x\in \left( -\infty ;0 \right)$.

Идём далее. В следующем задании нас поджидают десятичные дроби:

А что нужно делать с десятичными дробями в показательных неравенствах? Правильно: избавляться от них, переводя в обыкновенные. Вот и мы переведём:

Ну и что мы получили в основаниях показательных функций? А получили мы два взаимно обратных числа:

Таким образом исходное неравенство можно переписать так:

Разумеется, при умножении степеней с одинаковым основанием их показатели складываются, что и произошло во второй строчке. Кроме того, мы представили единицу, стоящую справа, тоже в виде степени по основанию 4/25. Осталось лишь выполнить рационализацию:

Заметим, что $\frac<4><25>-1=\frac<4-25> <25>\lt 0$, т.е. второй множитель является отрицательной константой, и при делении на неё знак неравенства поменяется:

Наконец, последнее неравенство из текущего «комплекта»:

В принципе, идея решения тут тоже ясна: все показательные функции, входящие в состав неравенства, необходимо свести к основанию «3». Но для этого придётся немного повозиться с корнями и степенями:

С учётом этих фактов исходное неравенство можно переписать так:

Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:

Вот и всё. Окончательный ответ: $x\in \left( -\infty ;3 \right)$.

Выделение устойчивого выражения и замена переменной

В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. Чтобы справиться с ними, необходимо вспомнить правила работы со степенями. В частности — вынесение общих множителей за скобки.

Но самое главное — научиться понимать: что именно можно вынести за скобки. Такое выражение называется устойчивым — его можно обозначить новой переменной и таким образом избавиться от показательной функции. Итак, посмотрим на задачи:

Начнём с самой первой строчки. Выпишем это неравенство отдельно:

Заметим, что $<<5>^>=<<5>^>=<<5>^>\cdot 5$, поэтому правую часть можно переписать:

Заметим, что никаких других показательных функций, кроме $<<5>^>$, в неравенстве нет. И вообще, нигде больше не встречается переменная $x$, поэтому введём новую переменную: $<<5>^>=t$. Получим следующую конструкцию:

Возвращаемся к исходной переменной ($t=<<5>^>$ ), а заодно вспоминаем, что 1=5 0 . Имеем:

Вот и всё решение! Ответ: $x\in \left[ -1;+\infty \right)$. Переходим ко второму неравенству:

Здесь всё то же самое. Заметим, что $<<3>^>=<<3>^>\cdot <<3>^<2>>=9\cdot <<3>^>$. Тогда левую часть можно переписать:

Вот примерно так и нужно оформлять решение на настоящих контрольных и самостоятельных работах.

Что ж, попробуем что-нибудь посложнее. Например, вот такое неравенство:

В чём тут проблема? Прежде всего, основания показательных функций, стоящих слева, разные: 5 и 25. Однако 25 = 5 2 , поэтому первое слагаемое можно преобразовать:

Как видите, сначала мы всё привели к одинаковому основанию, а затем заметили, что первое слагаемое легко сводится ко второму — достаточно лишь разложить показатель. Теперь можно смело вводить новую переменную: $<<5>^<2x+2>>=t$, и всё неравенство перепишется так:

И вновь никаких трудностей! Окончательный ответ: $x\in \left[ 1;+\infty \right)$. Переходим к заключительному неравенству в сегодняшнем уроке:

Первое, на что следует обратить внимание — это, конечно, десятичная дробь в основании первой степени. От неё необходимо избавиться, а заодно привести все показательные функции к одному и тому же основанию — числу «2»:

Отлично, первый шаг мы сделали — всё привели к одному и тому же основанию. Теперь необходимо выделить устойчивое выражение. Заметим, что $<<2>^<4x+8>>=<<2>^<4x+6+2>>=<<2>^<4x+6>>\cdot 4$. Если ввести новую переменную $<<2>^<4x+6>>=t$, то исходное неравенство можно переписать так:

Естественно, может возникнуть вопрос: каким это образом мы обнаружили, что 256 = 2 8 ? К сожалению, тут нужно просто знать степени двойки (а заодно степени тройки и пятёрки). Ну, или делить 256 на 2 (делить можно, поскольку 256 — чётное число) до тех пор, пока не получим результат. Выглядеть это будет примерно так:

\[\begin & 256=128\cdot 2= \\ & =64\cdot 2\cdot 2= \\ & =32\cdot 2\cdot 2\cdot 2= \\ & =16\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =8\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =4\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2= \\ & =<<2>^<8>>.\end\]

То же самое и с тройкой (числа 9, 27, 81 и 243 являются её степенями), и с семёркой (числа 49 и 343 тоже было бы неплохо запомнить). Ну, и у пятёрки тоже есть «красивые» степени, которые нужно знать:

Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.

Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)

Источник