Способы решения неполных квадратных уравнений 8 класс

Содержание

Неполные квадратные уравнения
Основные понятия
Решение неполных квадратных уравнений
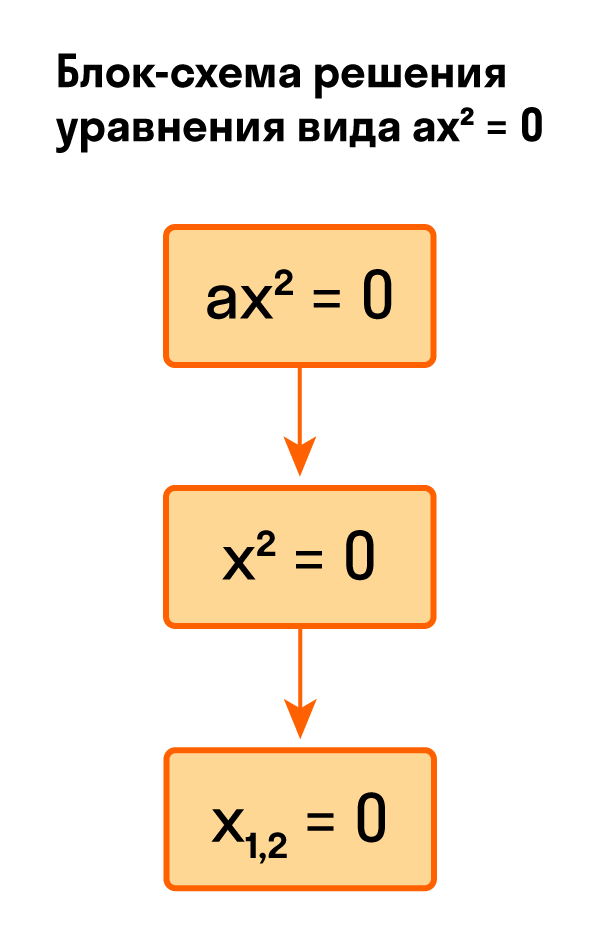
Как решить уравнение ax² = 0
Как решить уравнение ax² + с = 0
В двух словах
Как решить уравнение ax² + bx = 0
Неполные квадратные уравнения
теория по математике 📈 уравнения
Неполное квадратное уравнение при b=0: ax 2 +c=0
Неполное квадратное уравнение при с=0: ax 2 +bx=0
Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0
Конспект урока по алгебре в 8 классе по теме «Решение неполных квадратных уравнений»
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Оставьте свой комментарий
Безлимитный доступ к занятиям с онлайн-репетиторами
Подарочные сертификаты

Неполные квадратные уравнения

О чем эта статья:

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:

Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса!

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а 0.

Пример 1. Найти решение уравнения 9x² + 4 = 0.

Разделим обе части на 9:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Разделим обе части на -1:

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² — 32x = 0

Это уравнение равносильно х = 0 и 2x — 32 = 0.

Решить линейное уравнение:

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² — 12x = 0

Разложить левую часть уравнения на множители и найти корни:

Источник

Неполные квадратные уравнения

теория по математике 📈 уравнения

Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где х – переменная, a, b, c некоторые числа, причем a≠0. Обычно его называют полным квадратным уравнением.

Если в таком уравнении один из коэффициентов b или c равен нулю, либо оба одновременно равны нулю, то такое уравнение называется неполным квадратным уравнением.

Неполное квадратное уравнение при b=0: ax 2 +c=0

Для решения такого вида уравнения надо выполнить перенос коэффициента с в правую часть, затем найти квадрат переменной (делим обе части на одно и то же число), найти два корня уравнения, либо доказать, что корней нет (если х 2 равен отрицательному коэффициенту; знаем, что квадрат любого числа равен только положительному числу).

Пример №1. Решить уравнение:

Выполним перенос числа –45 в правую часть, изменяя знак на противоположный: 5х 2 =45; найдем переменную в квадрате, поделив обе части уравнения на 5: х 2 =9. Видим, что квадрат переменной равен положительному числу, поэтому уравнение имеет два корня, находим их устно, извлекая квадратный корень из числа 9, получим –3 и 3. Оформляем решение уравнения обычным способом:

Ответ: х=±3 или можно записать ответ так: х₁=–3, х₂=3 (обычно меньший корень записывают первым). Пример №2. Решить уравнение:

Выполним решение уже известным способом: –6х 2 =90. х 2 =–15 Здесь видим, что квадрат переменной равен отрицательному числу, а это значит, что уравнение не имеет корней. Ответ: нет корней. Пример №3. Решить уравнение:

Здесь мы видим в левой части уравнения формулу сокращенного умножения (разность квадратов двух выражений). Поэтому, можем разложить данное выражение на множители, и найти корни уравнения: (х–10)(х+10)=0. Соответственно, вспомним, что произведение двух множителей равно нулю тогда, когда хотя бы один из множителей равен нулю, то есть х–10=0 или х+10=0. Откуда имеем два корня х₁=10, х₂=–10.

Неполное квадратное уравнение при с=0: ax 2 +bx=0

Данного вида уравнение решается способом разложения на множители – вынесением за скобки переменной. Данное уравнение всегда имеет два корня, один из которых равен нулю. Рассмотрим данный способ на примерах.

Пример №4. Решить уравнение:

Выносим переменную х за скобки: х(х+8)=0. Получаем два уравнения х=0 или х+8=0. Отсюда данное уравнение имеет два корня – это 0 и –8.

Пример №5. Решить уравнение:

Здесь кроме переменной можно вынести за скобки еще и коэффициент 3, который является общим множителем для данных в уравнении коэффициентов. Получим: 3х(х–4)=0. Получаем два уравнения 3х=0 и х–4=0. Соответственно и два корня – нуль и 4.

Неполное квадратное уравнение с коэффициентами b и с равными нулю: ax 2 =0

Данное уравнение при любых значениях коэффициента а будет иметь один корень, равный нулю.

Пример №6. Решить уравнение:

Обе части уравнения делим на (–14) и получаем х 2 =0, откуда соответственно и единственный корень – нуль. Пример №6. Решить уравнение:

Также делим обе части на 23 и получаем х 2 =0. Значит, корень уравнения – нуль.

Источник

Конспект урока по алгебре в 8 классе по теме «Решение неполных квадратных уравнений»

Научиться решать неполные квадратные уравнения различных видов.

Составить алгоритм для решения неполных квадратных уравнений.

Научиться находить уравнение равносильное данному.

Отработать алгоритм решения неполных квадратных уравнений.

Тип урока: урок открытия нового знания.

Познавательные: анализировать, делать выводы, сравнивать объекты по способам действий.

Регулятивные: определять цель, проблему, выдвигать версии, планировать деятельность.

Коммуникативные: излагать свое мнение, использовать речевые средства,

Личностные: осознавать свои эмоции, вырабатывать уважительное отношение к одноклассникам.

Предметные: умение на выполнении задания построить алгоритм для решения уравнений каждого вида.

Метапредметные : умение выдвигать гипотезы, предположения, видеть различные способы решения задачи.

Личностные: умение правильно излагать свои мысли, понимать смысл поставленной задачи

Учебник, компьютер, проектор, презентация, карточки для творческого задания и самостоятельной работы.

Организационный момент 1. Приветствие 2. Проверка наличия всех нужных учебных пособий для урока

Какое уравнение называется квадратным?

Как называются коэффициенты квадратного уравнения?

Может ли коэффициент а равняться нулю?

Какое квадратное уравнение называется неполным?

Какое уравнение называется приведённым квадратным уравнением?

Определите коэффициент уравнения.

а) 6х 2 – х + 4 = 0

б) 12х — х 2 + 7 = 0

Укажите, какие из данных уравнений являются квадратными.

а) 2х 2 + 7х – 3 = 0;

в) – х 2 – 5х – 1 = 0.

Разложите на множители и укажите правильный ответ.

Восстановите квадратные уравнения по его коэффициентам.

5) а = 3 b = -4 c = 0

На основании материала устной работы учащиеся формулируют тему, цель и задачи урока.

Постановка проблемной ситуации.

У вас на столах есть карточки с заданиями, которые я попрошу вас выполнить.

Задание для первой группы:

х ₁ = ; х ₂ = —.

х 2 = — нет корней.

Задание для второй группы:

х ₁ = 0 или 4х + 9 = 0

х ₂ =

Задание для третьей группы:

Создают общую таблицу для решения всех видов уравнений и таблицу видов неполных квадратных уравнений.

Решение заданий № 518(а,б), № 515(д) стр. 120-121 учебника.

х ₁ = 0 или 2х + 3 = 0

2х = -3; х ₂ = — 1,5. Ответ: 0; -1,5.

х 2 =

х ₁ = ; х ₂ = .

6 v 2 = — 24 – нет корней.

Самостоятельная работа с самопроверкой.

а) ;

б) ;

в) .

а) ;

б) ;

в) .

а) ;

б) ;

в) .

Ответы к самостоятельной работе.

п. 21; № 515 (б, г, е); № 521 (а, в). Дополнительно: № 522 (б, г).

Что вы нового узнали на уроке?

Как мы решали поставленные задачи?

Что мы для этого использовали?

Что вы еще хотите для себя узнать нового на следующих уроках?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 832 человека из 77 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 297 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 609 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-517725

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Пензенские родители смогут попасть в школы и детсады только по QR-коду

Время чтения: 1 минута

Минобрнауки разработало концепцию преподавания истории российского казачества

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник