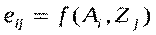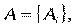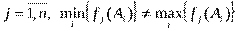Лекция 5.Многокритериальные методы принятия управленческих решений
1. Принятие управленческих решений в условиях полной определенности.
2. Принятие управленческих решений в условиях неопределенности и риска.
1. Принятие управленческих решений в условиях полной определенности.
Проблема управления деятельностью предприятия заключается в определении различных альтернатив действий и выборе оптимальной альтернативы, т. е. такой, которая позволяет получить наилучший результат в достижении поставленной цели.
В качестве альтернатив могут выступать новые целевые области (товарные рынки), виды выпускаемой продукции, инвестиции в различные сферы деятельности предприятия и т. д. Как правило, они не могут быть реализованы одновременно.
Целенаправленный выбор среди подобных альтернатив представляет собой принятие управленческого решения.
Реализация (осуществление) любой возможной альтернативы ведет к одному или нескольким последствиям (результатам). Ожидаемыми результатами могут быть выручка от реализации товаров, издержки производства, доля удовлетворения спроса, прибыль, затраты на продвижение товара, доля рынка и др.
На значение результата обычно оказывают влияние разнообразные факторы. Возможное положение дел, не зависящее напрямую от воздействия руководства предприятия, называется ситуацией внешней или окружающей среды. Состояние внешней среды складывается, как правило, в результате имеющейся политической обстановки (стабильная, нестабильная), поведения конкурирующих фирм (реактивное. нереактивное поведение), социально-экономических условий (платежеспособного спроса, правительственного регулирования экономики и т. д.). Состояния внешней среды в теории принятия решений называют обычно гипотезами.
Каждой реализуемой альтернативе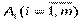 
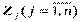
соответствуют некоторые состояния окружающей среды 
. Ожидаемый результат eij при выборе альтернативы Aiи принятии гипотезы Zjполучается, если применить функцию предпочтения, или, как чаще всего говорят, функцию полезности f, т.е.:
Значения функции fнаглядно представляются в виде так называемой матрицы ожидаемых результатов. При этом могут задаваться вероятности появления ситуаций внешней среды (гипотез)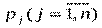 
, которые при принятии решений считаются рисками.
Таким образом, проблема принятия решения может быть сведена к получению необходимой информации, размещению ее в виде таблиц, например в виде табл. 1. представляющих собой по существу основные модели задач теории принятия решений, и выбору оптимальной альтернативы.
Матрица описания задач принятия решений
| Альтернативы, Аi | Состояния внешней среды, Zj (гипотезы) | |||
| Z1 | Z2 | …. | Zn | |
| А1 | e11 | e12 | …. | e1n |
| А2 | e21 | e22 | …. | e1n |
| …. | …. | |||
| Аm | em1 | em2 | …. | emn |
| Вероятности гипотез, pj | p1 | p2 | …. | Pn |
Здесь eijозначает ожидаемый результат от применения альтернативы Ai при наступлении состояния внешней среды Zj.
Если в матрице решений имеется доминирующая альтернатива, то она и выбирается в качестве оптимального решения.
Однако, как правило, доминирующие альтернативы отсутствуют и, кроме того, решение приходится принимать в условиях риска и неопределенности. Здесь нужны специальные принципы принятия решений, или решающие правила, или критерии принятия решений, которые используются иногда как синонимы.
Ниже рассмотрим методы принятия решений:
а) в условиях полной определенности, когда известны все составляющие и характеристики проблемы управления;
б) в условиях вероятностной определенности (риска);
в) в условиях неопределенности.
Необходимо различать однокритериальные и многокритериальные методы выбора управленческих решений.
1. Однокритериальные методы выбора управленческих решений.
• исходное множество альтернатив 
• оценки результатов выбираемых альтернатив f(Ai);
· критерий выбора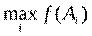 
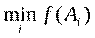
или 
.
Следовательно, выбор характеризуется однозначной связью между принятым решением Ai и его результатом f(Ai). В процессе решения задачи определяется альтернатива A*, для которой f(A*)=max f(Ai) или f(A*)=min f(Ai).
2. Многокритериальные методы выбора управленческих решений.
В достаточно большом количестве практических случаев принятия решений при планировании действий приходится учитывать не один, а несколько критериев. Можно считать, что все критерии стремятся к максимуму, так как если некоторые критерии минимизируются, то путем умножения их на (-1) они будут стремиться к максимуму, причем решение при этом не изменяется.
Матрица исходных данных принятия решений имеет вид (табл. 2).
Матрица исходных данных для многокритериальных методов выбора
| Альтернативы, Аi | Критерии (цели) | |||
| Z1 | Z2 | …. | Zn | |
| А1 | e11 | e12 | …. | e1n |
| А2 | e21 | e22 | …. | e1n |
| …. | …. | |||
| Аm | em1 | em2 | …. | emn |
| Значимость критерия, αj | α1 | α2 | …. | αn |
В случае многокритериальной оптимизации возникают три проблемы.
Первая проблема связана с выбором принципа оптимальности. В математическом отношении эта проблема эквивалентна задаче упорядочения векторных множеств, а выбор принципа оптимальности — выбору отношений порядка.
Вторая проблема связана с нормализацией векторного критерия F(х). Дело в том, что частные критерии имеют различные единицы измерения, поэтому их необходимо привести к единому масштабу измерения, т. е. нормализовать(обычно приводят к безразличным величинам).
Третья проблема связана с учетом приоритета (степени важности) частных критериев. Часто для учета приоритета вводится вектор распределения важности или значимости критериев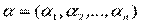 
.
Рассмотрим методы многокритериальной оптимизации:
1. Метод равномерной оптимизации:
(1)
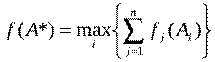
Он применяется, если глобальное качество альтернативы представляет собой сумму локальных (частных) качеств и, кроме того, все критерии имеют одну и ту же единицу измерения, например денежное выражение либо безразмерные величины. Главный недостаток метода -это возможность компенсации малых значений некоторых критериев достаточно большими значениями других.
2. Метод справедливого компромисса:
(2)
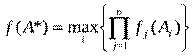
3. Метод свертывания критериев:
(3)
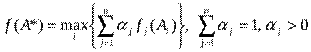
Здесь каждому из критериев приписываются весовые коэффициенты αj
4. Метод главного критерия:
(4)
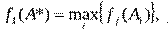
Здесь f1(х) — главный (наиболее важный из всех) критерий.
5. Метод идеальной точки. Ищется план, удовлетворяющий условию:
(5)
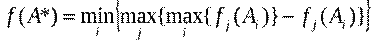
На первом этапе применяется метод нормализации критериев (получение безразмерной формы критериев).
Так как критерии могут иметь различные масштабы и шкалы измерения, то прежде, чем приступить к решению многокритериальной задачи, их необходимо привести к одной единице измерения (обычно к безразмерному виду). Этот процесс называется нормализацией. Существуют различные методы нормализации, Предлагается следующий способ получения безразмерной формы критериев:
(6)
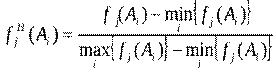
где 
Рассмотрим пример многокритериальной задачи управления. Пусть фирма имеет возможность реализовывать свои товары на 4-х различных рынках (альтернативы А1, А2, А3, А4). При этом ставятся одновременно следующие цели: минимизация затрат на рекламу, завоевание максимальной доли рынка и максимальный объем продаж в течение планируемого периода. Исходные данные приведены в табл. 3.
Источник
Многокритериальный выбор управленческих решений
В задачах принятия решений часто возникает необходимость оценки выбора по многим показателям, характеризующим различные стороны их качества и конкретизирующим понятие «достижение целей».
Формулировка целей решения проблем производится обычно в общей содержательной форме. Поэтому конкретизация целей осуществляется путем введения совокупности показателей достижения целей. Важным требованием, предъявляемым к показателям, является их измеримость.
Формулировка критерия выбора в виде максимальной степени достижения целей конкретизируется, как достижение экстремальных (max или min) значений показателя.
Следовательно, критериями выбора оптимального решения становятся экстремальные значения показателей достижения целей.
В связи с этим для случая индивидуального ЛПР рассматриваемая задача получила название многокритериального выбора. Для группового ЛПР эта задача называется групповым многокритериальным выбором.
При построении многокритериальных моделей принятия решений должны учитываться следующие основные положения [33]:
· модель создается исследователем для структуризации и уточнения лица, принимающего решения, которое непосредственно участвует в ее разработке;
· модель должна быть логически непротиворечива;
· модель должна давать возможность использовать реальную информацию о задаче, полученную от экспертов, ЛПР;
· модель должна быть достаточно простой и удобной для анализа и использования ЛПР.
Под критериями принимают такие показатели, которые:
· признаются ЛПР в качестве характеристик степени достижения поставленной цели;
· являются общими и измеримыми для всех допустимых решений;
· характеризуют общую ценность решений таким образом, что у ЛПР имеется стремление получать по ним наиболее предпочтительные оценки (то есть в качестве критериев не следует использовать ограничения).
Критерии, применяемые для решения многокритериальных задач, должны отвечать следующим принципам:
· минимальности – постановочная часть задачи должна содержать как можно меньшее число критериев, а отбрасывание хотя бы одного из них меняет результат;
· измеримости – каждый критерий должен допускать возможность количественной (в крайнем случае, качественной) оценки степени достижения соответствующей цели;
· неповторимости, то есть разные критерии не должны учитывать одну и ту же сторону решения;
· четкости, при которой каждый критерий должен иметь понятную для ЛПР формулировку, ясный и однозначный смысл, характеризовать определенный аспект решения.
Эти требования, конечно, противоречивы, но ясное представление о них позволяет строить полноценный набор критериев. При этом есть необходимость указать на некоторые частные и типичные пробелы, наблюдаемые в анализе многокритериальных задач принятия решений:
· нет полного списка допустимых решений;
· нет полного списка критериев, характеризующих качества решений;
· не построены все или некоторые шкалы критериев;
· нет оценок вариантов решений по шкалам критериев;
· нет решающего правила, позволяющего получить требуемое в задаче упорядочение вариантов решения (решающее правило, метод принятия решения, представляет собой принцип сравнения векторных оценок и формирования суждения о предпочтительности одних из них по отношению к другим).
Известно, что возможности человека по переработке многомерной информации очень ограничены, поэтому вероятность ошибочных действий ЛПР достаточно велика. В рамках рассматриваемого подхода были предложены два варианта проверки действий ЛПР.
Первый – критерий непротиворечивости: в аналогичных ситуациях оценки или сравнения альтернатив руководитель должен принимать одинаковые решения. Этот критерий основан на предположении о существовании у ЛПР определенной, непротиворечивой политики. Отметим, что при всей естественности такого предположения, при всей очевидной его справедливости в реальных ситуациях так бывает не всегда.
Второй критерий для оценки деятельности ЛПР – критерий транзитивности, который для трех альтернатив А, В, С можно записать так:
1) Если А > В, B > C, то A>C (для отношения предпочтения);
2) Если А=В, В=С, то А=С (для отношения безразличия).
При нарушении транзитивности возникает порочный круг типа A>B, B>C, C>A и выделить предпочтительный вариант невозможно.
Как и в случае с первым критерием, надо сказать, что в реальных ситуациях появление нетранзитивности в предпочтениях ЛПР вполне возможно.
В специальной литературе обсуждаются как причины появления противоречивости и нетранзитивности, так и способы выхода из этих достаточно сложных ситуаций. Здесь же отметим, что для ЛПР имеет смысл сознательно избегать нарушения указанных критериев.
Известно, что для человека сложными являются:
· задачи с большой нагрузкой на понятийный аппарат;
· задачи, требующие параллельной обработки многомерной информации;
· задачи сравнения альтернатив с малыми уровнями различимости;
· задачи, имеющие значительное число критериев (5-6-7 и больше);
· показатели со значительным числом оценок на шкалах критериев (5 и больше);
· показатели с большим числом результирующих классов решений (5-6 и больше).
Характерными для такого подхода, о котором сейчас идет речь, являются следующие особенности. Для описания ситуаций принятия решения используется естественный язык данной организации: понятия хуже» и «лучше» для каждого критерия формулируются в виде развернутых словесных определений.
При сборе информации используются лишь такие вопросы, для которых заранее была установлена возможность получения надежных, непротиворечивых ответов. На основе опыта и интуиции ЛПР определены общие правила оценки вариантов, определен перечень критериев оценивания.
Во многих случаях целесообразно использовать шкалы качественных критериев со словесными оценками градаций качества. При этом можно ввести в рассмотрение достаточно сложные понятия: описать большое число факторов, имеющих отношения к рассматриваемой ситуации; можно учесть неопределенность, связанную с неполным знанием последствий принимаемых решений, и риск, связанный с выбором некоторых альтернатив.
Критерии с качественными шкалами, оценки по которым четкие, однозначные, хорошо различимые, являются эффективным средством получения информации от экспертов, повышают достоверность этой информации, так как эксперт рассматривает альтернативные варианты через призму предпочтения ЛПР.
Словесные шкалы оценок соответствуют изменению качества от лучшего к худшему значению. Эти шкалы – порядковые. Надо заметить, что использование этих шкал не исключает перехода к количественным оценкам, скажем, с использованием аппарата размытых, нечетких множеств, о котором речь шла выше.
При использовании шкал качественных критериев человек обычно может последовательно и непротиворечиво определять превосходство среди объектов, отличающихся оценками по двум критериям. Если по остальным критериям оценки объектов одинаковы и являются либо лучшими, либо худшими (число критериев при этом может достигать 7-8 штук, а число оценок по каждому из них может достигать 5-6 штук).
С помощью экспертов обычно получают ответ на вопрос, какая ситуация хуже при поочередном ухудшении качества по каждому из рассматриваемых критериев.
По результатам ответов можно построить единую шкалу оценок для данной пары критериев. Эту процедуру можно повторить для всех других пар критериев, причем одновременно идет проверка предпочтения на непротиворечивость и транзитивность.
Полученная информация представляет собой соответствующие двум ситуациям (сначала лучшие оценки по фиксированным критериям, затем худшие) системы линейных неравенств и равенств, отображающие сравнения падений качества вдоль осей разных критериев. В результате возникает множество доминирующих или несравнимых альтернатив. Если их исключить из множества всех альтернатив, то среди оставшихся можно снова выделить доминирующие или несравнимые и т.д.
В итоге получают группы лучших, средних, худших альтернатив, которые позволяют ЛПР принять решение.
Конечно, использование формальных методов, в частности ИСО (исследование операций), существенно повышает качество принимаемых решений.
В случае, если все показатели могут быть измерены в одной и той же шкале и приведены к одной единице измерения, например, денежной оценке, то решение такой задачи является элементарной. Здесь задача характеризуется набором вариантов решений, предпочтения которых оцениваются одним обобщенным показателем. Значения этого показателя упорядочивают решения по предпочтительности, поэтому оптимальное решение определяется на основе одного критерия, соответствующего экстремуму обобщенного показателя.
В большинстве случаев не удается достаточно просто свести показатели достижения целей к одному обобщенному. Поэтому задача выбора заключается в определении оптимального решения с учетом всей совокупности показателей. В связи с этим возникает необходимость их согласования с целью выработки наилучшего решения.
В таких случаях попытки конкретизировать цель выливаются обычно в составление некоторого списка требований, состоящего из набора Ui (х,у), (i=1,2, …, n) частных показателей эффективности (критериев), совокупное увеличение которых и представляется оперирующей стороне целью операции (оптимизации). Однако эти частные показатели (критерии), как правило, оказываются несогласованными, то есть увеличение одних из них может привести к уменьшению других, что делает проблему оптимального выбора противоречивой и неоднозначной.
Например, разработчикам приходится оценивать некоторый план только по двум критериям (если показателей больше, то сложность оценки увеличивается): прибыль и трудоемкость.
Если какое-то изменение плана улучшает некий показатель, но при этом ухудшает какой-то другой показатель, то планы не сопоставимы. Зато они становятся сопоставимыми, если все показатели одного плана лучше (или скорее не хуже) всех показателей другого плана. Иначе говоря, вполне возможно считать оптимальным такой план, в котором нельзя улучшить ни один показатель, не ухудшив при этом какого-то другого показателя. Скажем, найден план с прибылью 10 тыс. у.е. и трудоемкостью 15 тыс. чел.-дн. И всякая попытка изменить этот план или снижает прибыль или увеличивает трудоемкость. По Парето, такой план оптимален.
Однако, с другой стороны, почти в любой задаче планирования много оптимумов Парето и вопрос равнозначен решению первоначальной задачи, то есть дело по сути не сдвинулось с места.
В теории ИСО, в которых цель операции выражается столь неопределенно, что не может быть отражена в едином критерии эффективности, обычно называют многокритериальными.
Одним из распространенных, но, к сожалению, малоэффективных способов борьбы с многокритериальностью является так называемое свертывание частных критериев в некоторый единый критерий.
Наиболее распространенные способы свертывания частных критериев следующие:
· способ формирования цели качественного типа;
· обобщенное логическое свертывание;
1. Способ формирования цели качественного типа. Под качественными целями понимаются цели, которые могут быть только или достигнуты, или не достигнуты. все результаты операции, приводящие к достижению, одинаково хороши; точно так же все результаты, не приводящие к достижению цели, одинаково неудовлетворительны.
Критерий эффективности в этом случае принимает два значения, например: 1 – в случае успеха и 0 – в противоположном случае.
Свертывание частных критериев в качественный тип осуществляется разбиением множества значений частных критериев на удовлетворительные и неудовлетворительные.
Назначаются некоторые числа Ui ° (I=1,2, …, n), и удовлетворительными значениями объявляются только такие, для которых
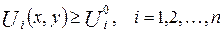 . | (6.7) |
При этом критерий–свертка может быть выражен через некоторый функционал W — критерий эффективности*:
 . | (6.8) |
Этот способ образования единого критерия наиболее доступен пониманию оперирующей стороны, так как ближе всего отражает смысл требований, налагаемых на значения частных критериев. Однако трудности корректного назначения чисел 
так, чтобы не потерять наиболее эффективные способы действий или не попасть в область недостижимых значений, делают эту процедуру не менее противоречивой и неоднозначной, чем стремление к одновременному увеличению значений всех частных критериев.
2. Логическое свертывание. Если частные критерии Ui(x,y) являются критериями качественного типа, принимающими только значения 0 или 1, то для их свертывания можно использовать два подхода логических операций:
а) конъюнкция. Единая цель состоит в выполнении всех частных целей:
 ; | (6.9) |
б) дизъюнкция. Единая цель состоит в выполнении хотя бы одной из частных целей:
 . | (6.10) |
Это наиболее конструктивный способ свертывания частных критериев. Однако он имеет ограниченное применение, так как годен для качественных целей.
1. Обобщенное логическое свертывание. Прямым обобщением действий предыдущего пункта является вместо (6.9) следующее выражение:
 | (6.11) |
и вместо (6.10) выражение:
 | (6.12) |
где li – значения весовых коэффициентов критериев.
Эти способы свертывания применимы для любых типов критериев. Выражение (6.11) немедленно превращается в (6.9), если все Ui(x,y) принимают только значения 0; 1, а li=1. точно так же в этом случае (6.12) эквивалентно (6.10).
Трудности, связанные с таким типом свертывания, обусловлены неопределенностью при выборе конкретных значений весовых коэффициентов li, однако такого типа свертки могут оказаться чрезвычайно полезными при решении сложных задач теории ИСО.
2. Линейное свертывание. Единый коэффициент эффективности представляют в виде линейной комбинации частных критериев:
 | (6.12) |
Этот способ обычно называют экономическим способом свертывания, так как весовые коэффициенты li часто выступает в роли цен на i-й товар и W представляет собой суммарную выручку. Назначение конкретных значений коэффициентов li, как и в способе 3 (обобщенное логическое свертывание), также вызывает немалые затруднения.
В теории ИСО имеется большой класс многокритериальных задач, когда частные критерии Ui не зависят от неопределенных факторов У. В этом случае стремление увеличивать значение каждого из частных критериев не столь уже противоречиво, если проводить процедуру достаточно корректно (см. работу Краснощекова П.К.).
Данный подход можно использовать при решении проблем проектирования сложных технических систем и объектов, что, к сожалению, носит узконаправленный характер и применять его для решения экономических задач, где слишком велико значение факторов У, проблематично. Поэтому при принятии управленческих решений часто склоняются к выработке единого комплексного показателя эффективности, который, для ранее приведенного примера в наших рассуждениях, может быть представлен в виде:
 | (6.13) |
где Пр – прибыль, Т – трудозатраты, а l1 и l2 – весовые коэффициенты, показывающие относительную важность каждого показателя и уравнивающие размерности.
Для отыскания весовых коэффициентов часто используют метод экспертных оценок, если ЛПР и разработчики затрудняются с их назначением.
Иногда разработчики применяют так называемый «метод последовательных уступок» [8].
Решение задачи обычно осуществляется в следующем порядке:
· рассматриваемые критерии ранжируются по приоритетности;
· формулируются целевые функции по каждому критерию;
· определяется оптимум по критерию, находящемуся на первой ступени приоритетности;
· производится корректировка полученного результата в соответствии со следующей по рангу целевой функцией и переходят аналогичным образом к последующей.
Такими последовательными действиями в форме корректировок и ищут оптимальные решения по нескольким целевым функциям.
Теоретическая сложность решения многокритериальных задач заставляет исследователей-практиков искать методы и подходы, способствующие получению приемлемых результатов.
Эти результаты, безусловно, менее точны, чем те, которые могут быть получены с помощью формальных методов, но они вполне отвечают главному требованию решения любой управленческой задачи – это выбору лучшего действия или получению приемлемого результата.
Исходя из этих соображений, на практике применяют два подхода, которые проиллюстрированы на примере принятия решений по обновлению продукции производства (см. книгу первую, часть 3, гл. 8.3).
В процессе выработки решения ЛПР приходится неоднократно сталкиваться с трудностями, которые в одиночку бывает разрешить весьма сложно. В этих случаях руководитель часто прибегает к групповому (коллективному) выбору решений. Данный подход может привести если не к окончательному выбору альтернативы, то, по крайней мере, оказывает несомненную помощь ЛПР в последующих действиях. Исходя из этих позиций, думается целесообразно рассмотреть сущность группового выбора и правила большинства.
Источник
