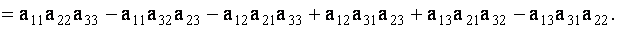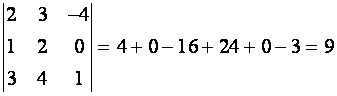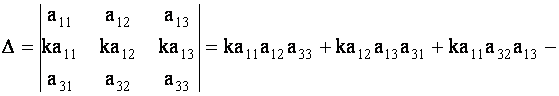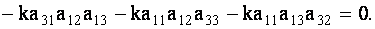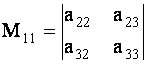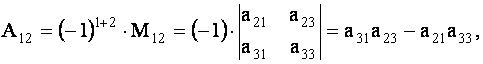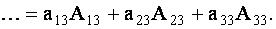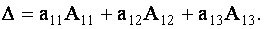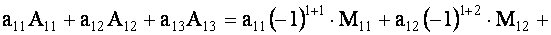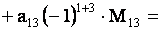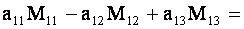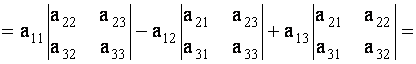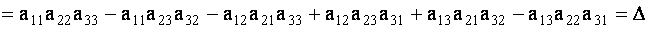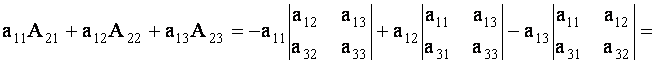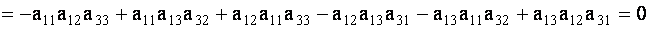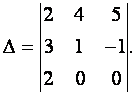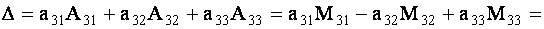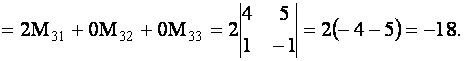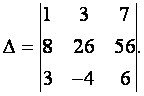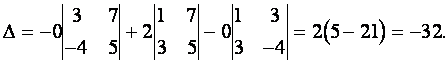Математика — онлайн помощь
Пусть дана квадратная матрица третьего порядка
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
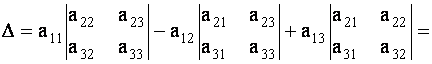 | (1.7) |
Определитель третьего порядка обозначается символом
 | (1.8) |
где числа 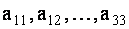
Индексы 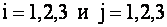
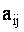
Например, элемент 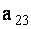
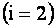
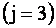
Элементы 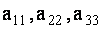
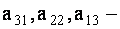
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором 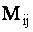
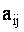
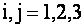
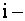
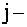
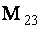
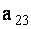
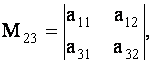
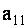
С помощью миноров определитель (7) можно записать в виде
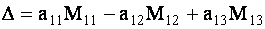 | (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением 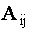
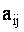
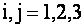
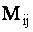
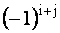
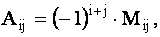 где где  / / | (1.10) |
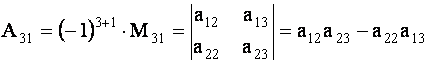
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
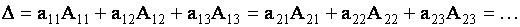 | (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы 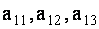
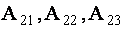
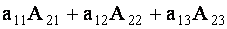
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим 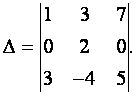
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Найти определитель матрицы третьего порядка
Вы будете перенаправлены на Автор24
Существует несколько способов нахождения определителей матриц третьего порядка. Рассмотрим их подробнее.
Перечислим основные способы, используемые для этого:
- Правило Саррюса;
- Правило треугольников;
- Использование специальной формулы для вычисления;
- Использование метода Гаусса или иначе метода перестановок.
Правило Саррюса
Правило Саррюса для вычисления матриц 3-ьего порядка применяется просто: достаточно соответственно рисунку переписать 2 первых столбика справа рядом с матричной таблицей, а затем записать произведения, стоящие по диагоналям со знаками.
Если диагональ идёт сверху слева вниз направо — то произведение записывается со знаком «+», а если диагональ идёт из правого верхнего угла в нижний левый — то со знаком «-».
Рисунок 1. Формула третьего порядка. Автор24 — интернет-биржа студенческих работ
Дана матричная таблица $A$. Вычислите детерминант с помощью правила Саррюса.
$A = \begin
Решение:
Рисунок 2. Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ
$Δ = 0 \cdot 4 \cdot 3 + 3 \cdot 2 \cdot 2 – 1 \cdot 1 \cdot 5 – 3 \cdot 1 \cdot 3 – 0 \cdot 2 \cdot 5 + 1 \cdot 4 \cdot 2 = 0 + 12 – 5 — 9 – 0 + 8 = 6$
Правило треугольников
Это правило немного похоже на предыдущее. Суть его в том, что произведения элементов с главной диагонали и двух треугольников, задействующих все остальные элементы как показано на рисунке, записываются со знаком плюс, а произведения элементов с побочной диагонали и двух синих треугольников — с противоположным.
Готовые работы на аналогичную тему
Рисунок 3. Треугольники. Автор24 — интернет-биржа студенческих работ
Найдите определитель из прошлого задания, используя метод треугольников.
Решение:
Рисунок 4. Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ
$Δ= 0 \cdot 4 3 + 3 \cdot 2 \cdot 2 – 1 \cdot 5 \cdot 1 + 1 \cdot 4 \cdot 2 – 1 \cdot 3 \cdot 3 – 2 \cdot 5 \cdot 0 = 0 + 12 – 5 + 8 – 9 – 0 = 6$
Использование формулы разложения по строчке
Для матрицы 3 на 3, приведённой выше, определитель можно сосчитать по формуле:
$Δ =\begin
Разложите определитель матрицы из предыдущих примеров по 1-ой строчке и найдите его.
Решение:
$Δ = 0 \cdot \begin
Метод Гаусса
Чтобы вычислить детерминант этим методом, нужно используя разрешённые преобразования получить треугольную матрицу.
Разрешёнными преобразованиями являются сложение и вычитание строчек и столбцов, в то время как при перестановке строчек и столбцов между собой необходимо помнить о смене знака определителя в конце.
После этого нужно перемножить элементы, стоящие на главной диагонали, их произведение и будет определителем.
Примените метод Гаусса для получения детерминанта матрицы из предыдущих примеров.
Решение:
$A = \begin
Переставим первую строчку со второй, при этом запомним, что знак детерминанта в конце поменяется:
Вычтем из третьей строчки 1-ую, умноженную на 2:
Сложим между собой третью строчку со второй:
Получили искомый вид матрицы. Теперь можно сосчитать определитель, минус появляется из-за перемены строчек местами:
$Δ=-\begin
Источник