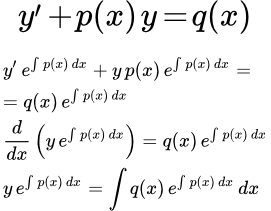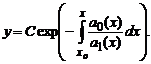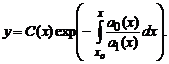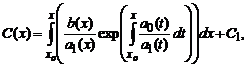Способы решения линейного дифференциального уравнения первого порядка

Решение линейных дифференциальных уравнений первого порядка

Определения и методы решений

Линейное дифференциальное уравнение первого порядка – это уравнение вида
,
где p и q – функции переменной x .

Линейное однородное дифференциальное уравнение первого порядка – это уравнение вида
.

Линейное неоднородное дифференциальное уравнение первого порядка – это уравнение вида
.

Член q ( x ) называется неоднородной частью уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим обе части исходного уравнения (1) на интегрирующий множитель
:
(2)
Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (2):

Интегрируем:

Умножаем на . Получаем общее решение линейного дифференциального уравнения первого порядка:

Пример решения линейного дифференциального уравнения первого порядка

Разделим обе части исходного уравнения на x :
(i) .
Тогда
;
.
Интегрирующий множитель:

Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ± 1 ).
Умножим (i) на x 3 :
.
Выделяем производную.
;
.
Интегрируем, применяя таблицу интегралов:
.
Делим на x 3 :
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 22-07-2012 Изменено: 25-02-2015

Источник

Способы решения линейного дифференциального уравнения первого порядка

Использование интегрирующего множителя;

Метод вариации постоянной.

Если линейное дифференциальное уравнение записано в стандартной форме: \[y’ + a\left( x \right)y = f\left( x \right),\] то интегрирующий множитель определяется формулой: \[u\left( x \right) = \exp \left( <\int > \right).\] Умножение левой части уравнения на интегрирующий множитель \(u\left( x \right)\) преобразует ее в производную произведения \(y\left( x \right) u\left( x \right).\)

Общее решение диффференциального уравнения выражается в виде: \[y = \frac <<\int + C>><>,\] где \(C\) − произвольная постоянная.

Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения : \[y’ + a\left( x \right)y = 0.\] Общее решение однородного уравнения содержит постоянную интегрирования \(C.\) Далее мы заменяем константу \(C\) на некоторую (пока еще неизвестную) функцию \(C\left( x \right).\) Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию \(C\left( x \right).\)

Описанный алгоритм называется методом вариации постоянной . Разумеется, оба метода приводят к одинаковому результату.

Если, кроме дифференциального уравнения, задано также начальное условие в форме \(y\left( <> \right) = ,\) то такая задача называется задачей Коши .

Решение задачи Коши не содержит произвольной константы \(C.\) Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие \(y\left( <> \right) = .\)

Будем решать данную задачу методом вариации постоянной. Сначала найдем общее решение однородного уравнения: \[xy’ = y,\] которое решается разделением переменных: \[ ><> = y,>\;\; <\Rightarrow \frac<> = \frac<>,>\;\; <\Rightarrow \int <\frac<>> = \int <\frac<>> ,>\;\; <\Rightarrow \ln \left| y \right| = \ln \left| x \right| + \ln C,>\;\; <\Rightarrow y = Cx.>\] где \(C\) − произвольное положительное число.

Теперь заменим константу \(C\) на некоторую (пока неизвестную) функцию \(C\left( x \right)\) и далее будем искать решение исходного неоднородного уравнения в виде: \[y = C\left( x \right)x.\] Производная равна \[y’ = <\left[ \right]^\prime > = C’\left( x \right)x + C\left( x \right).\] Подставляя это в дифференциальное уравнение, получаем: \[ \right] = C\left( x \right)x + 2,>\;\; <\Rightarrow C'\left( x \right)+ \cancel = \cancel + 2,>\;\; <\Rightarrow C'\left( x \right) = 2x.>\] Интегрируя, находим функцию \(:\) \[C\left( x \right) = \int <2xdx>= + ,\] где \(\) − произвольное действительное число.

Таким образом, общее решение заданного уравнения записывается в виде: \[y = C\left( x \right)x = \left( <+ > \right)x = + x.\]

\(A.\;\) Сначала решим данную задачу с помощью интегрирующего множителя . Наше уравнение уже записано в стандартной форме. Поэтому: \[a\left( x \right) = — 2.\] Тогда интегрирующий множитель имеет вид: \[ > \right) > = <\exp \left( <\int <\left( < - 2>\right)dx> > \right) > = <>.> \] Общее решение исходного уравнения записывается в виде: \[ + C>><> > = <\frac<<\int <>xdx> + C>><<>>>.> \] Вычислим последний интеграл, применяя интегрирование по частям. \[ <\int <\underbrace <>>_ \underbrace x_pdx> > = <\left[ <\begin<*<20>> <\int = qp — \int >\\

\\ >,\;q = — \frac<1><2>>> \end> \right] > = < - \frac<2>> — \int <1 \cdot \left( < - \frac<1><2>>> \right)dx> > = < - \frac<2>> + \frac<1><2>\int <>dx> > = < - \frac<2>> — \frac<1><4>> > = < - \frac<1><4>>\left( <1 + 2x>\right).> \] Получаем \[y = \frac<< - \frac<1><4>>\left( <1 + 2x>\right) + C>><<>>> = — \frac<1><4>\left( <1 + 2x>\right) + C>.\] \(B.\;\) Теперь сконструируем решение методом вариации постоянной . Рассмотрим соответствующее однородное уравнение \[y’ — 2y = 0\] и найдем его общее решение: \[ <\frac<><> = 2y,>\;\; <\Rightarrow \frac<> = 2dx,>\;\; <\Rightarrow \int <\frac<>> = 2\int ,>\;\; <\Rightarrow \ln \left| y \right| = 2x + C,>\;\; <\Rightarrow \left| y \right| = > = > = >,>\;\; <\Rightarrow y = \pm > = C>,> \] где \(C\) вновь обозначает произвольное действительное число. Заметим, что при \(C = 0\) мы получаем решение \(y = 0\) которое также удовлетворяет однородному уравнению.

Далее предположим, что \(C\) является функцией \(x\) и подставим решение \(y = C\left( x \right)>\) в исходное неоднородное уравнение. Выражение для производной имеет вид: \[y’ = <\left[ >> \right]^\prime > = C’\left( x \right)> + C\left( x \right) \cdot 2>.\] Следовательно, \[ > + \cancel<2C\left( x \right)>> — \cancel<2C\left( x \right)>> = x,>\;\; <\Rightarrow C'\left( x \right) = >x,>\;\; <\Rightarrow C\left( x \right) = \int <>xdx> .> \] Этот интеграл уже был найден в пункте \(A\), поэтому, можно записать: \[C\left( x \right) = — \frac<1><4>>\left( <1 + 2x>\right) + C.\] В результате, общее решение неоднородного дифференциального уравнения выражается формулой: \[ > > = <\left[ < - \frac<1><4>>\left( <1 + 2x>\right) + C> \right]> > = < - \frac<1><4>\left( <1 + 2x>\right) + C>.> \] Как видно, оба метода приводят к одному и тому же ответу.

Будем решать данный пример методом вариации постоянной. Для удобства запишем уравнение в стандартной форме: \[y’ + \frac = — \frac<2><<>>.\] Разделим обе части на \(<>.\) Очевидно, что корень \(x = 0\) не является решением уравнения.

Сначала вычислим интегрирующий множитель, который записывается в виде \[u\left( x \right) = \right)dx> >> = >>.\] Здесь \[ <\int <\tan xdx>= \int <\frac<<\sin x>><<\cos x>>dx> > = < - \int <\frac<\right)>><<\cos x>>> > = < - \ln \left| <\cos x>\right|.> \] Следовательно, интегрирующий множитель определяется формулой: \[ >> > = <\right|>> > = <\left| <\cos x>\right|.> \] Мы можем взять функцию \(u\left( x \right) = \cos x\) в качестве интегрирующего множителя. Легко убедиться, что левая часть уравнения после умножения на интегрирующий множитель становится производной произведения \(y\left( x \right)u\left( x \right):\) \[ <\left( \right)\cos x > = = = <<\left( \right)^\prime > > = <<\left[ \right]^\prime >.> \] Тогда общее решение заданного уравнения записывается следующим образом: \[ <>\left[ <\int + C> \right] > = <\frac<1><<\cos x>>\left[ <\int <\cos x\sin xdx>+ C> \right] > = <\frac<1><<2\cos x>>\int <\sin 2xdx>+ \frac<<\cos x>> > = < - \frac<<\cos 2x>><<4\cos x>> + \frac<<\cos x>> > = <\frac<<4\cos x>>\left( <4 - \cos 2x>\right).> \] Теперь определим постоянную \(C,\) которая удовлетворяет начальному условию \(y\left( 0 \right) = 1:\) \[ <<4\cos 0>>\left( <4 - \cos 0>\right) > = <\frac<<4 \cdot 1>>\left( <4 - 1>\right) > = <\frac<<3C>> <4>= 1.> \] Отсюда следует, что \(C = \large\frac<4><3>\normalsize.\)

Следовательно, решение задачи Коши выражается формулой: \[y = \frac<1><<3\cos x>>\left( <4 - \cos 2x>\right).\]

Видно, что данное уравнение не является линейным по отношению к функции \(y\left( x \right).\) Однако мы можем попытаться найти решение для обратной функции \(x\left( y \right).\) Запишем заданное уравнение через дифференциалы и сделаем некоторые преобразования: \[ + 2x> \right)\frac<><>,>\;\; <\Rightarrow ydx = 2dy + 2xdy,>\;\; <\Rightarrow y\frac<><> = 2 + 2x,>\;\; <\Rightarrow \frac<><> — \frac<2>x = 2.> \] Мы получили линейное дифференциальное уравнение по отношению к функции \(x\left( y \right).\) Решим его с помощью интегрирующего множителя: \[ > \right)dy> >> > = <>> >> > = <> > = <<<<<\left| y \right|>^2>>>>> > = <<<>>>> > = <\frac<1><<>>.> \] Общее решение в виде обратной функции \(x\left( y \right)\) выражается формулой: \[ + C>><> > = <\frac<<\int <\frac<1><<>> \cdot 2dy> + C>><<\frac<1><<>>>> > = <\frac<<\int <2ydy>+ C>><<\frac<1><<>>>> > = <\left( <+ C> \right).> \]

Источник

Линейные уравнения первого порядка

Назначение сервиса . Онлайн калькулятор можно использовать для проверки решения однородных и неоднородных линейных дифференциальных уравнений вида y’+y=b(x) .

• Решение онлайн
• Видеоинструкция

Теорема. Пусть a₁(x) , a₀(x) , b(x) непрерывны на отрезке [α,β], a₁≠0 для ∀x∈[α,β]. Тогда для любой точки (x₀, y₀), x₀∈[α,β], существует единственное решение уравнения, удовлетворяющее условию y(x₀) = y₀ и определенное на всем интервале [α,β].
Рассмотрим однородное линейное дифференциальное уравнение a₁(x)y’+a₀(x)y=0 .
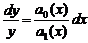
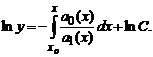
Разделяя переменные, получаем , или, интегрируя обе части, Последнее соотношение, с учетом обозначения exp(x) = e x , записывается в форме

Попытаемся теперь найти решение уравнения в указанном виде, в котором вместо константы C подставлена функция C(x) то есть в виде

Подставив это решение в исходное, после необходимых преобразований получаем 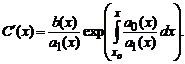Интегрируя последнее, имеем

где C₁— некоторая новая константа. Подставляя полученное выражение для C(x), окончательно получаем решение исходного линейного уравнения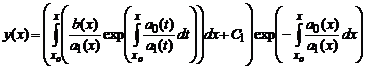
.

Описанный метод решения называется методом Лагранжа или методом вариации произвольной постоянной (см. также Метод вариации произвольной постоянной решения линейных неоднородных уравнений).

Пример . Решить уравнение y’ + 2y = 4x . Рассмотрим соответствующее однородное уравнение y’ + 2y = 0 . Решая его, получаем y = Ce -2 x . Ищем теперь решение исходного уравнения в виде y = C(x)e -2 x . Подставляя y и y’ = C'(x)e -2 x — 2C(x)e -2 x в исходное уравнение, имеем C'(x) = 4xe 2 x , откуда C(x) = 2xe 2 x — e 2 x + C₁ и y(x) = (2xe 2 x — e 2 x + C₁)e -2 x = 2x — 1 + C₁e -2 x — общее решение исходного уравнения. В этом решении y₁(x) = 2x-1 — движение объекта под действием силы b(x) = 4x, y₂(x) = C₁e -2 x -собственное движение объекта.

Пример №2 . Найти общее решение дифференциального уравнения первого порядка y’+3 y tan(3x)=2 cos(3x)/sin 2 2x.
Это неоднородное уравнение. Сделаем замену переменных: y=u•v, y’ = u’v + uv’.
3u v tg(3x)+u v’+u’ v = 2cos(3x)/sin 2 2x или u(3v tg(3x)+v’) + u’ v= 2cos(3x)/sin 2 2x
Решение состоит из двух этапов:
1. u(3v tg(3x)+v’) = 0
2. u’v = 2cos(3x)/sin 2 2x
1. Приравниваем u=0, находим решение для 3v tg(3x)+v’ = 0
Представим в виде: v’ = -3v tg(3x)

Интегирируя, получаем:

ln(v) = ln(cos(3x))
v = cos(3x)
2. Зная v, Находим u из условия: u’v = 2cos(3x)/sin 2 2x
u’ cos(3x) = 2cos(3x)/sin 2 2x
u’ = 2/sin 2 2x
Интегирируя, получаем:
Из условия y=u•v, получаем:
y = u•v = (C-cos(2x)/sin(2x)) cos(3x) или y = C cos(3x)-cos(2x) ctg(3x)

Источник