Способы решения геодезических задач

Что такое обратная и прямая геодезическая задача: суть, методы решения, назначение

В строительстве большую часть времени занимают геодезические работы. Это комплекс различных измерений и вычислений на местности. Стоит ли говорить, что качество выполненных работ зависит от точности полученных результатов. Это влияет на размещение зданий и сооружений, а также возведение их конструктивных элементов. Все должно соответствовать проектным показателям и техническим регламентам. Геодезические работы выполняются в объеме, определенном особенностями объекта и стадией его реализации. Компания «Промтерра» специализируется на их проведении с составлением необходимых чертежей, схем и расчетов. Для этого есть все составляющие: действующая лицензия, опыт, допуск СРО, штат специалистов. Один из вопросов, который поступает при выполнении работ, касается геодезической задачи. Что это такое, как используется в работе и ее назначение.

Математика в действии

По своей сути геодезические задачи — это математика в чистом виде. Основная задача состоит в определении взаимного положения точек принадлежащих какой-либо поверхности. Наиболее часто приходится иметь дело с прямыми и обратными геодезическими задачами, но на этом математические вычисления не заканчиваются. В зависимости от поставленных условий могут применяться и другие виды. Например, решение треугольника по измеренным углам и сторонам. Интересный исторический факт: с геодезическими задачами исследователи этой темы работают уже больше трех веков, а споры относительно методов дальше продолжаются.

Что такое прямая геодезическая задача

Эта разновидность предполагает вычисление координат, то есть широты и долготы определенной точки. А она, в свою очередь, лежит на математически правильной поверхности — земном эллипсоиде. Вычисления производятся по координатам другой точки, по длине и азимуту геодезической линии. Точность решения зависит от корректности исходных данных. Для проведения вычислений используют формулы нахождения приращений и определения координат.

Специалисты применяют разные методы для получения результатов. Наиболее востребованными считаются косвенный и прямой. Они отличаются тем, что в основе лежит точность исходных данных. Косвенные методы решения очень чувствительны к ним. Если в исходнике есть значительные расстояния, изменения по азимуту, то вычисления не получится сделать, или они будут с большими погрешностями. Прямые методы работают по соотношениям сфероидической геодезии, поэтому результаты можно получить более точные. Кстати, прямой тип геодезических задач применяется при вычислении координат в теодолитном ходе.

Что такое ОГЗ: суть обратной геодезической задачи

При работе над обратной геодезической задачей вычисления проводятся по известным координатам двух точек на земном эллипсоиде. Это нужно для получения значений горизонтального положения линий между ними, а также дирекционного угла этой самой линии. В этом состоит суть. Для получения искомых величин используется вычисление румба и расстояние между координатами точек. Нужно помнить, что дирекционный угол при этом находится по четверти системы координат, которая и является объектом, где размещены искомые позиции. Для решения нужно учитывать знаки приращения, которые свойственны для определенных четвертей. В этом типе задач уделяют большое значение сходимости результатов, поэтому расчеты могут проводиться несколько раз. На это влияют свойства горизонтального положения между точками. В каких случаях применяется обратная геодезическая задача? В тех, когда по известным двум точкам и их координатам определяют расстояние не только между ними, но и дирекционный угол линии.

В том или ином виде геодезические задачи возникают и в других направлениях — в полигонометрии, триангуляции, но на этом не заканчивается востребованность. Используется также, когда стоит задача определения взаимного положения точек по исходным данным длины и направления соединяющей линии. Есть ряд случаев, когда геодезические задачи решают с использованием формул аналитической геометрии в пространстве. Речь идет о пространственных прямоугольных координатах. Для этого используют пространственные компоненты направления прямой линии между этими точками.

Обратный тип геодезической задачи — не просто математическая проверка и вычисления. Она имеет практическое значение, ведь используется при вычислении длин проектных линий. Кроме этого, используется при выполнении привязки теодолитных ходов к пунктам геодезической сети, съемочных сетей и сетей сгущения. Еще одно практическое назначение — определение направления с пункта на пункт при отсутствии видимости. Обратная геодезическая задача используется в промышленном и гражданском строительстве.

А как решать обратные задачи, если в исходнике большие расстояния? В этом случае рекомендуется использовать метод итерации. Его можно использовать при расстояниях до 20 000 км. Итерация основана на решении прямой геодезической задачи любым выбранным методом — численным или аналитическим. И точность решения именно ОГЗ определяется решением ПГЗ.

Прямые и обратные геодезические задачи требуют получения точных результатов. Насколько получится достичь поставленной цели, зависит от исходных сведений и выбранного метода решения. Вычисление способом Бесселя, методом Рунге-Кутта-Фельберга, итерации, численного интегрирования — в каждом отдельном случае выбор зависит от расстояний и координат точек. В штате компании «Промтерра» работают опытные специалисты в сфере инженерной геодезии, поэтому за решение даже самых сложных задач можно быть спокойными. Тема геодезических задач всегда остается актуальной, поэтому отслеживание последних тенденций в проведении вычислений для получения точных результатов — необходимость. Важно отметить, что подобного плана математические методы востребованы не только в геодезической сфере деятельности, но и в навигации, корректировке ракетного огня и др.

Источник

Лекция № 6. Решение геодезических задач на поверхности эллипсоида

Виды геодезических задач и точность их решения.

Пути решения прямой и обратной геодезических задач.

Виды геодезических задач и точность их решения.

Сущность почти всех видов геодезических задач на поверхности эллипсоида состоит в определении геодезических координат точки по заданным координатам других точек и по измеренным или заданным угловым и линейным величинам.

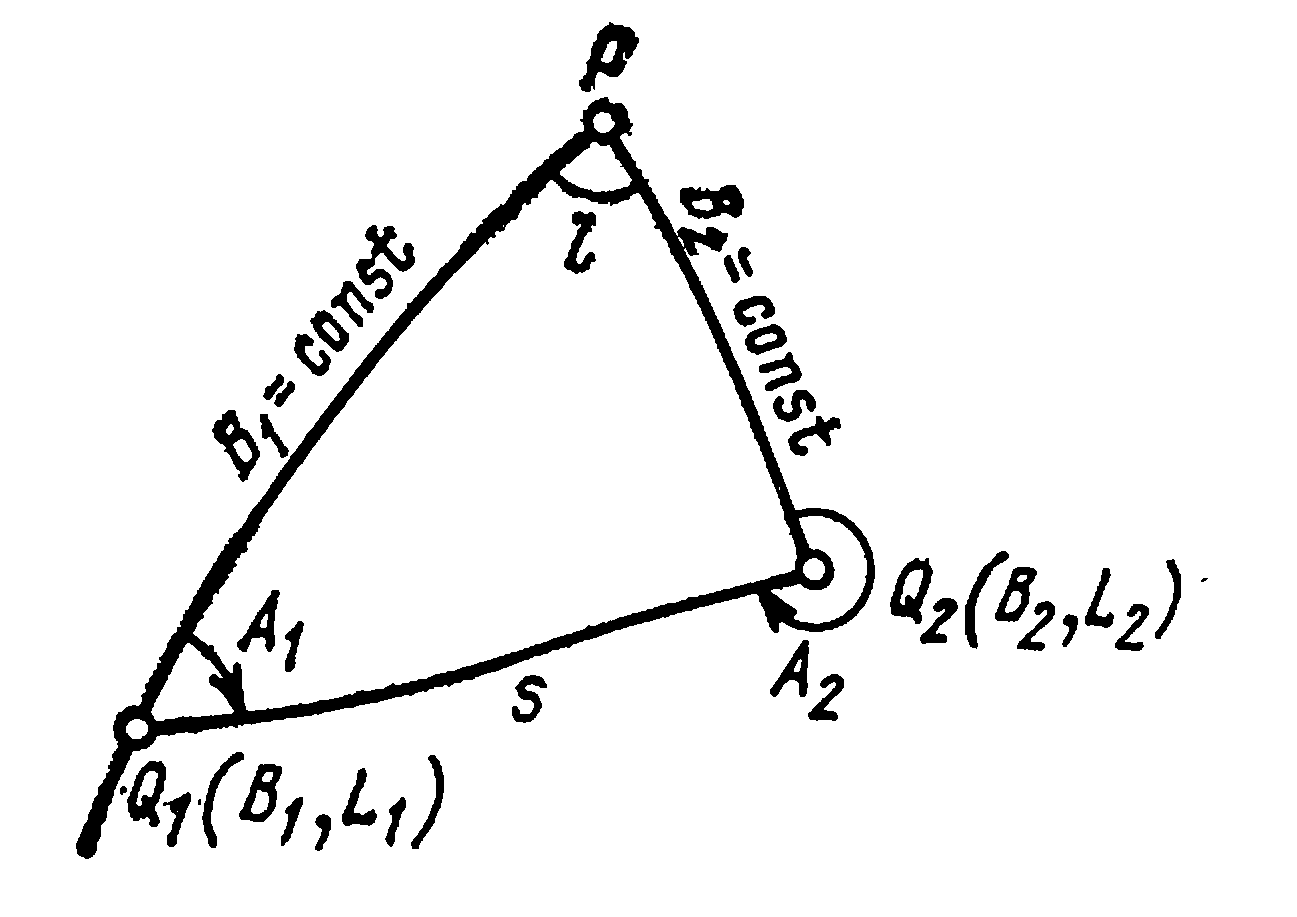
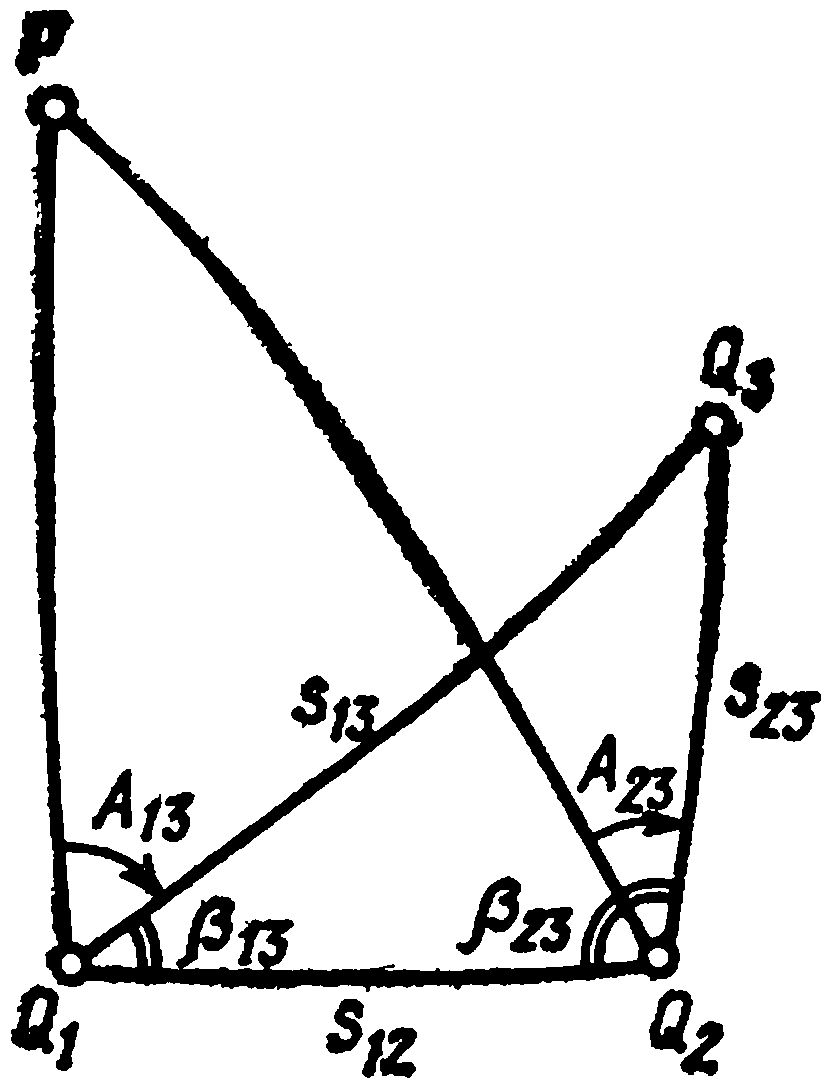
Между точкамиQ₁ и Q₂ на поверхности проведена геодезическая линия.

Точка Q₁ – начальная точка геодезической линии.

Точка Q₂ – конечная точка геодезической линии.

Геодезическая линия от точки Q₁ к точке имеет прямое направление, а от точки Q₂ к точке Q₁ – обратное направление.

В любой точке геодезической линии её азимут называется прямым, если он указывает прямое направление, и обратным, если он указывает обратное направление этой линии. Прямой и обратный азимуты в одной и той же точке отличаются на 180 о .

Прямой азимут в начальной точке называют также начальным азимутом геодезической линии.

Прямая геодезическая задача.

Даны геодезические координаты В₁ и L₁ некоторой точки Q₁, а также длина геодезической линии s и её начальный азимут А₁. По этим данным требуется найти координаты В₂ и L₂, а также обратный азимут А₂ в точке Q₂.

Обратная геодезическая задача.

Даны геодезические координаты В₁, L₁ и В₂, L₂ двух точек Q₁ и Q₂. Требуется найти кратчайшее расстояние s (длину геодезической линии) между заданными точками, а также прямой А₁и обратный А₂ азимуты этой линии в точках Q₁ и Q₂.

В обратной задаче геодезические координаты не определяются а задаются, поэтому её решение используют для контроля решения прямой геодезической задачи.

Вместе с тем она имеет и большое самостоятельное значение. Она широко применяется при решении многих технических задач в которых требуется определить расстояние и направление между двумя любыми точками на земной поверхности.

Прямую и обратную геодезические задачи называют главными геодезическими задачами.

Прямая геодезическая задача применяется при вычислении геодезических координат пунктов триангуляции 1 класса. В результате решения треугольников в сети 1 класса в каждом треугольнике будут известны все углы и все длины сторон. Для одного из пунктов, принятого за начальный, должны быть известны геодезические координаты В₀, L₀ и азимут А₀ с начального пункта на один из соседних пунктов.

Зная координаты начального пункта, а также расстояния и азимуты на соседние пункты, вычисляют геодезические координаты и обратные азимуты всех других пунктов, непосредственно связанных с начальным пунктом. Принимая затем каждый из этих пунктов за начальный. Вычисляют геодезические координаты и обратные азимуты соседних с ним пунктов и т.д.

Разнообразия в расстояниях, по которым возникает необходимость решения главных геодезических задач, различные требования к точности не позволяют рекомендовать какой-либо единый метод и единые формулы. Поэтому, в зависимости от указанных условий, целесообразно применять различные методы и формулы решения задач. Условно расстояния можно разделить на четыре группы:

Малые расстояния – до 30-45 км.

Средние расстояния – до 600 км.

Большие расстояния – до 5000 км.

Очень большие расстояния – до 19000 км.

При развитии государственной сети геодезических пунктов прямая и обратная геодезические задачи применяются для малых расстояний (20 – 60 км, в редких случаях 200 – 300 км). В специальных целях такие задачи приходится решать на любые расстояния вплоть до 20 000 км.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

РЕШЕНИЕ ИНЖЕНЕРНО-ГЕОДЕЗИЧЕСКИХ ЗАДАЧ

При выполнении проектных и разборчивых работ в геодезической практике возникает необходимость решения различных инженерно-геодезических задач.

1. Закрепление точки с проектной отметкой обычно осуществляют геометрическим нивелированием. Данная задача является наиболее распространенной при всякого рода строительстве. Положение точки в плане должно быть обозначено на местности, и вблизи ее должен располагаться постоянный или временный репер с известной высотой (рис.35).

Рис. 35. Вынос проектной отметки

Установив нивелир посередине между репером и точкой, проектную высоту которой необходимо перенести на местность, по рейке, установленной на репере, определяют горизонт прибора (инструмента)

ГИ = (62)

а затем вычисляют отсчет по рейке на искомой точке В:

.

В месте вынесения проектной высоты устанавливают рейку, опуская ее или поднимая таким образом, чтобы получить расчетный отсчет b. В момент установления отсчета b забивают кол до уровня пятки рейки, высота которого будет соответствовать 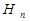. Контроль заключается в повторном выносе.

2. Построение линий с проектным уклоном (рис.36) осуществляют при строительстве дорог, улиц, подземных коммуникаций. Для этого устанавливают проектную высоту начальной точки А и конечно точки В линии и обозначают их на местности.

Рис. 36. Вынос линии с заданным уклоном

Устанавливают нивелир непосредственно у точки А таким образом, чтобы один из подъемных винтов прибора совпадал с направлением АВ. Измеряют высоту прибора i над точкой А. Наводят прибор на точку В и наклоняют трубу подъемным винтом до тех пор, пока отсчет по рейке, установленной в точке В, не будет равен b = i. Лучше всего для выноса линии с проектным уклоном использовать теодолит.

3. Определить высоты сооружения можно разными способами. Наиболее простым является способ тригонометрического нивелирования, который рассмотрим ниже.

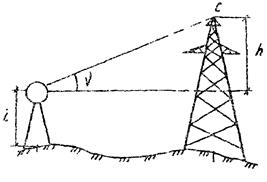
Для определения высоты необходимо измерить расстояние до препятствия d (рис.37) или определить засечкой, высоту прибора i и вертикальный угол v при наведении перекрестия сетки нитей теодолита на наивысшую точку сооружения, тогда высота определится:

= (63)

где — высота точки, над которой стоит теодолит.

Рис. 37. Определение высоты сооружения

В случае, когда расстояние d от точки стояния инструмента до сооружения невозможно измерить непосредственно, его можно вычислить по теореме синусов, применив прямую угловую засечку (рис.38):

(64)

(65)

Для выполнения инструментальных наблюдений и способе угловой засечки необходимо разбить базис, который должен быть измерен с высокой точностью, после чего приступают к измерению углов на точках А и В.

Рис. 38. Определение Рис. 39. К обратной геодезической

недоступного расстояния задаче на плоскости

4. Обратная геодезическая задача. В результате решения данной задачи определяют дирекционный угол и расстояние d между точками А и В, показанными на рис. 39.

По исходным координатам вычисляют приращения координат:

,

. (66)

Тогда из треугольника АКВ

, (67)

, (68)

. (69)

Если возникает необходимость определения только горизонтальной проекции расстояния между точками с известными координатами, то пользуются формулой:

. (70)

При вычислении по таблицам тригонометрических функций сначала определяют румб направления:

, (71)

. (72)

а затем вычисляют дирекционный угол.

Четверть	I	II	III	IV
Наименование четверти	СВ	ЮВ	ЮЗ	СЗ
Связь дирекционного угла и румба

Контролем решения ОГЗ будет служить сходимость результатов расстояний d, полученных из разных формул.

СПИСОК ЛИТЕРАТУРЫ

1. Инженерная геодезия / Под ред. Д. Ш. Михелева. — М.: Высш. шк., 2006.

2. Лабораторный практикум по инженерной геодезии: Учебн. пособие для вузов / В. Ф. Лукьянов, В. Е. Новак, Н. Н. Борисов [и др.]. – М.: Недра, 1990. – 334 с.

3. Практикум по геодезии [Текст] : учебное пособие для вузов / под ред. Г. Г. Поклада. — М. : Трикста : Академический Проект, 2011. — 487 с.

4. Федотов, Г. А. Инженерная геодезия [Электронный ресурс] : учебник / Г. А. Федотов. — 6-е изд. — М.: НИЦ ИНФРА-М, 2016. — 479 с. — (Высшее образование). — Режим доступа: http://znanium.com/bookread2.php?book=485299

5. Федотов, Г. А. Инженерная геодезия: учебник / Г. А. Федотов. – 3-е изд., испр. – М.: Высш. шк., 2006. — 463с.

Источник