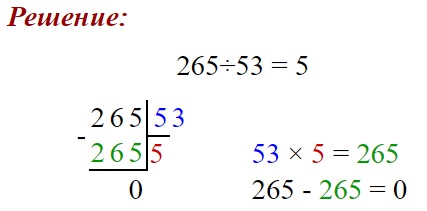Способы решения двузначных чисел

Деление на двузначное число — способы и примеры решений

Деление на двузначное число похоже на тот же процесс с однозначным числом, но занимает больше времени. Однако есть немало методов, которые упрощают процесс. Научиться выполнять деление быстро помогут основные правила и серьезная практика.

Деление на двузначное число устно

Осуществляется такое деление методом подбора. Например, нужно разделить число 90 на двузначное число 15 без остатка.

Чтобы это сделать устно, нужно подобрать такое число, которое при умножении его на 5 (15 оканчивается на 5) даст число, оканчивающееся на 0 (так как 90 оканчивается на ноль).

Какое число при умножении на 5 даст в результате число с цифрой 0 на конце? Их несколько.

Теперь проверяем. Если цифра нам подходит, то, умножив ее на 15, получим 90:

Последняя цифра 6 подходит. Мы выполнили деление: 90 : 15 = 6.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

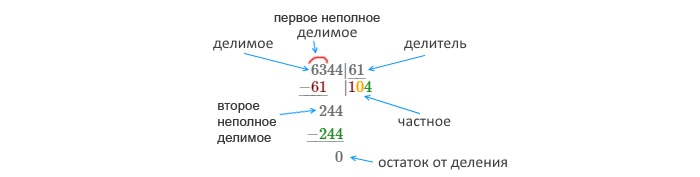
На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Примеры деления в столбик на двузначное число

Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.

Пример 1

Найдём значение частного чисел 265 и 53:

Пример 2

Найдем результат деления чисел 624 и 52:

Пример 3

Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:

Пример 4

Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:

Пример 5

Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:

Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.

Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.

Источник

Как объяснить ребенку сложение и вычитание двухзначных чисел

Обучать ребенка арифметике довольно непросто, ведь она состоит из трёх этапов. Для начала придется разобраться с числами от 0 до 9, а потом со всем остальным. Однако и с двузначными числами нужно работать поэтапно. Пусть ребенок отработает действия с числами от 10 до 20, затем от 20 до 30 и так далее. Если вы примените правильные методы и организуете обучение в игровой форме, ребенок быстрее усвоит сложную арифметику.

Итак, обучение проходит в несколько этапов.

Подготовка

На этом этапе ребенок учится складывать и вычитать двузначные числа. Пусть ребенок сначала поработает с круглыми числами (научится их складывать и вычитать). После научите его выделять в числах разрядные слагаемые (34=30+4). Попробуйте объяснить ему, что в числе 34 получится 3 десятка и 4 единицы. Справиться с этим вам помогут счетные палочки. Это довольно практичный метод, который применяется в школах уже давно.

Примите к сведению, что счетные палочки можно легко заменить на детали лего или какой-нибудь конструктор: мелкие детали— это единицы, детали покрупнее— это десятки. Сразу после этого можно переходить к сложению и вычитанию круглых чисел.

Сложение и вычитание круглых чисел

Существуют разные способы обучения ребенка сложению и вычитанию круглых чисел.

• Во-первых, когда ребёнок понимает, что 20 равняется двум десяткам, а 30– это три десятка, он быстро научится считать. 20+30 — это тоже самое, что два десятка и три десятка получается пять десятков.
• Во-вторых, можно тренироваться на том же конструкторе. Возьмите 2 детали среднего размера, добавьте к ним ещё 3 детали среднего размера— и получается 5 деталей среднего размера. Получается 20+30=50.

По такому же принципу разберите и вычитание круглых чисел. Как только малыш усвоит эти несложные манипуляции, можно двигаться дальше.

Складываем и вычитаем числа без перехода через разряд

Чтобы разобраться с этим этапом, придётся объяснять действия на практике. Скажем, нужно выполнить следующее действие: 24+31. Тут уж нам придется изучить ещё 1 способ сложения/вычитания. Выкладываем палочки по горизонтальной линии — это будут наши десятки; а вертикально выложенные палочки— это единицы. Теперь складываете вертикальные палочки с вертикальными, а горизонтальные с горизонтальными. Так выкладываем 2 палочки горизонтально и 4 вертикально, а рядом— 3 горизонтальные и 1 вертикальную палочку. Сложив их, получаем 5 горизонтальных палочек и 5 вертикальных, то есть, окончательный ответ 55. Постепенно ребёнок усвоит, что единицы нужно добавлять к единицам, а к десяткам добавляются десятки.

Следующее, что вы можете разобрать с малышом— это научиться складывать и вычитать в столбик. Здесь необходимо объяснить будущему школьнику, что единицы записываются под единицами, а десятки под десятками. Возможно, будет полезно вначале разложить кусочки лего и найти результат, а потом провести расчет в столбик.

Таким же образом можно разобрать и вычитание ( с помощью палочек, кусочков Лего и записи в столбик). Если ребенок освоил технику со сложением, ему будет не трудно справиться и с вычитанием.

Сложение и вычитание чисел с переходом через разряд

Сложность выполнения сложения и вычитания чисел через разряд заключается в том, что тут придётся «занимать» и «запоминать» числа.

Попробуем решить такой пример (26+35) с помощью палочек.

1. Выкладываем числа палочками и складываем их по разрядам. У нас выходит 5 горизонтальных и 11 вертикальных палочек.
2. Теперь напомните малышу, что, выполняя арифметические действия 10 единиц равняются 1 десятку. Получается, 10 вертикальных палочек можно заменить 1 горизонтальной палочкой.
3. Выходит 6 десятков и 1 единица.
4. Отсюда видно, что при сложении единиц, у нас есть число больше 10. Эти 10 единиц мы заменяем 1 десятком. Теперь показываем ребёнку, что выполняя сложение и вычитание, начинать нужно с единиц. И если их получается 10 и больше, выделяем здесь десяток и прибавляем его к другим десяткам.

Как только этот этап пройден, можно рассмотреть и другие варианты сложения двузначных чисел.

• сначала к числу добавляем десятки, а потом единицы. (26+30+5=61)
• первое слагаемое делаем круглым, затем добавляем к нему второе слагаемое и вычитаем то число, которое добавили изначально. (26+4=30; 30+35=65; 65-4=61)
• плюсуем единицы с единицами, а десятки с десятками. Помните, если единиц больше 10, то добавляем 1 десяток. (20+30=50; 6+5=11; 50+10=60) Итого получается 61.

Вычитание тоже покажите на наглядном примере. Допустим, 53-27.

1. Делаем первое число (5 десятков и 3 единицы) и второе (2 десятка и 7 единиц)
2. Мы видим, что из 3 единиц невозможно вычесть 7 единиц. Значит, занимаем 1 десяток = 10 единиц.
3. Теперь из 13 единиц мы можем вычесть 7 единиц. А теперь отнимаем десятки. Тут важно напомнить ребёнку, что десятков у нас стало на 1 меньше. Значит, от 4 мы отнимаем 2.
4. Итого у нас получается 13-7=6 и 4-2=2. Значит, получается 53-27=26.

Завершив наглядный метод, начните считать и другими способами:

• сначала вычитаем в столбик: напомните ребёнку, что единицы вычитаться и складываются с единицами, а десятки с десятками. 53-27=26
• а теперь вычитаем десятки, а после единицы.

Чтобы объяснить ребёнку тонкости арифметических действий, возьмите в помощь счёты. Это удобно и практично. А ещё ребёнок мог бы записать числа на них и практиковаться, пока не дойдёт до автоматизма.

Помните, что каждый ребёнок индивидуален и выбирать способ обучения необходимо исходя из особенностей ребенка. Кому-то легко дается счет на палочках, кто-то предпочитает считать в столбик. А кому-то для практики требуются месяца, ребёнок считает разными способами, но ему так и не удаётся научиться считать быстро и без ошибок. Родителям стоит быть терпеливыми, помогать малышу, решать примеры вместе и не злиться. Пусть он чувствует вашу поддержку и заботу. А с регулярной практикой у малыша обязательно все получится.

Источник

Как быстро считать в уме: приемы устного счета больших чисел

• 12 января 2021 г.
• 15 минут
• 279 402
• 9

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник