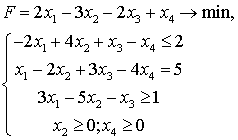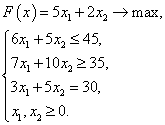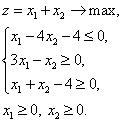Способы решения двойственных задач

Двойственные задачи линейного программирования

Двойственность является важным понятием в линейном программировании, имеющим экономическое (практическое) применение. Например, для задачи оптимального распределения ресурсов для производства некоторых видов товаров пара прямой и двойственной задачи принимает следующий экономический смысл:
Прямая задача: Сколько и какой продукции xj необходимо производить, чтобы при заданных доходах Cj и объемах ресурсов bi максимизировать доход от продажи продукции?
Двойственная задача: Какова должна быть «теневая» цена каждого ресурса yi, чтобы при заданных количествах bi и доходах Cj минимизировать затраты?

Для составления двойственных задач используют специальные правила, при решении же выбирают один из наиболее подходящих методов решения ЗЛП: симплекс-метод, графический метод. Более того, так как между парой двойственных задач существует связь, иногда достаточно решить только одну из задач, чтобы получить решение второй.

Примеры составления и решения двойственных задач линейного программирования приведены в этом разделе — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий — Решение контрольных по линейному программированию.

Примеры составления и решения двойственных задач онлайн

Задача 1. Записать математическую модель двойственной ЗЛП по заданной прямой:

Задача 2. Составить задачу, двойственную исходной задаче:

Задача 3. Решить задачу линейного программирования; составить задачу, двойственную данной, и также найти ее решение:

Источник

Решение двойственной задачи

Здесь мы рассмотрим вопрос, как из решения прямой задачи, получить решение двойственной задачи.

Теоремы двойственности

Первая теорема двойственности

Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная задача имеет оптимальное решение. При этом значения целевых функций прямой и двойственной задачи, для оптимальных решений, равны друг другу.

Если одна из пары двойственных задач не имеет решения вследствие неограниченности целевой функции, то двойственная задача не имеет решения вследствие несовместимости системы ограничений.

Вторая теорема двойственности

Пусть мы имеем симметричную пару двойственных задач (1) и (2):
(1.1) ;
(1.2)
(2.1) ;
(2.2)
Для того чтобы допустимые решения и являлись оптимальными решениями двойственных задач (1) и (2), необходимо и достаточно, чтобы выполнялись следующие равенства:
(3) , .
(4) , ;

Для наглядности, выпишем равенства (3) и (4) в развернутом виде:
(3.1)
(3.2)

(3.m)

Метод решения двойственной задачи

Применяя теоремы двойственности, можно получить решение двойственной задачи из решения прямой. Опишем метод решения двойственной задачи.

Пусть мы нашли решение прямой задачи (1) с оптимальным значением целевой функции и с оптимальным планом . Подставим найденные значения в систему ограничений (1.2). Тогда если -е неравенство не является равенством, то есть если
,
то, согласно (3.i),
.
Рассматривая все строки системы ограничений (1.2), мы найдем, что часть переменных двойственной задачи равна нулю.

Далее замечаем, что если , то, согласно (4.k), -я строка системы ограничений (2.2) является равенством:
.
Составив все строки системы ограничений (2.2), для которых , мы получим систему уравнений, из которой можно найти ненулевые значения переменных .

На основании первой теоремы двойственности, минимальное значение целевой функции
.

Если известно решение задачи (2), то аналогичным образом можно найти решение задачи (1).

Примеры решения двойственной задачи из решения прямой

Пример 1

Пусть дана задача линейного программирования:
;

Известно решение этой задачи:
; .

Составить двойственную задачу и получить ее решение из решения прямой.

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи.
(П1.1.1) ;
(П1.1.2) ;
(П1.1.3) ;
(П1.1.4) .
Поскольку первая и четвертая строки являются строгими неравенствами (не являются равенствами), то
и .

Поскольку и , то 2-я и 4-я строки двойственной задачи являются равенствами:

Подставим уже найденные значения и , имеем:

Отсюда
;
; .

Двойственная задача имеет вид:
;

Ее решение
;

Пример 2

Дана задача линейного программирования:
(П2.1.1) ;
(П2.1.2)
Найти решение этой задачи, решив двойственную задачу графическим методом.

Решение задачи (П2.2) приводится на странице “Решение задач линейного программирования графическим методом”. Решение задачи (П2.2) имеет вид:
; .

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи (П2.2).
;
;
.
Поскольку третья строка является строгим неравенством (не являются равенством), то
.

Поскольку и , то 1-я и 2-я строки двойственной задачи (П2.1) являются равенствами:

Подставим найденное значение .

Решаем систему уравнений.
;
;
;
; ;
.

Решение исходной задачи (П2.1) имеет вид:
; .

Автор: Олег Одинцов . Опубликовано: 27-08-2016

Источник

Решение двойственной задачи линейного программирования

С помощью данного онлайн-калькулятора можно получить:

• решение двойственной задачи линейного программирования через решений прямой задачи (симплексным методом, по теореме двойственности);
• оптимальный план двойственной задачи; оценки ресурсов (двойственные оценки);
• определение дефицитных и недефицитных (избыточных) ресурсов;
• изменение целевой функции при изменении параметров; обоснование эффективности оптимального плана;
• анализ устойчивости двойственных оценок (предельное изменение b_i, c_i); анализ субоптимальных вариантов плана.
• решение задачи о расшивке узких мест производства.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Основная идея теории двойственности: для каждой задачи линейного программирования (ЛП) существует некоторая задача ЛП, решение которой тесно связано с прямой. При этом:

• матрица ограничений двойственной задачи (ДЗ) есть транспонированная матрица прямой задачи;
• вектор «цен» для прямой задачи есть вектор правых частей ограничений задачи ДЗ и наоборот.

Общие правила составления двойственной задачи (более подробно):

Прямая	Двойственная
Целевая функция (max)	Правая часть ограничений
Правая часть ограничений	Целевая функция (min)
A — матрица ограничений	A T – матрица ограничений
i -ое ограничение: ≤ 0, (≥ 0)	Переменная yi ≥ 0, (≤ 0)
i -ое ограничение: = 0	Переменная yi≠ 0
Переменная xj ≥ 0 (≤ 0)	j -ое ограничение: ≤ 0 (≥ 0)
Переменная xj ≠ 0	j -ое ограничение: = 0

Пример . Определим максимальное значение целевой функции F(X) = 3x₁ +5x₂ +4x₃ при следующих условиях-ограничений.
0.1x₁ + 0.2x₂ + 0.4x₃≤1100
0.05x₁ + 0.02x₂ + 0.02x₃≤120
3x₁ + x₂ + 2x₃≤8000

Решим прямую задачу симплексным методом.
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных.
0.1x₁ + 0.2x₂ + 0.4x₃ + 1x₄ + 0x₅ + 0x₆= 1100
0.05x₁ + 0.02x₂ + 0.02x₃ + 0x₄ + 1x₅ + 0x₆= 120
3x₁ + 1x₂ + 2x₃ + 0x₄ + 0x₅ + 1x₆= 8000
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных: x₄ , x₅ , x₆
Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,1100,120,8000)
Поскольку задача решается на максимум, то ведущий столбец выбирают по максимальному отрицательному числу и индексной строке. Все преобразования проводят до тех пор, пока не получатся в индексной строке положительные элементы.
Переходим к основному алгоритму симплекс-метода.

План	Базис	В	x 1	x 2	x 3	x 4	x 5	x 6	min
1	x 4	1100	0.1	0.2	0.4	1	0	0	5500
x 5	120	0.05	0.02	0.02	0	1	0	6000
x 6	8000	3	1	2	0	0	1	8000
Индексная строка	F(X1)	0	-3	-5	-4	0	0	0	0

Итерация №0
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты
В качестве ведущего выберем столбец, соответствующий переменной x₂, так как наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления и из них выберем наименьшее:
Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен 0.2 и находится на пересечении ведущего столбца и ведущей строки. Формируем следующую часть симплексной таблицы. Вместо переменной x в план 1 войдет переменная x₂. Строка, соответствующая переменной x₂ в плане 1, получена в результате деления всех элементов строки x₄ плана 0 на разрешающий элемент РЭ=0.2. На месте разрешающего элемента в плане 1 получаем 1. >В остальных клетках столбца x₂ плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x₂ и столбец x₂.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
СТЭ — элемент старого плана, РЭ — разрешающий элемент (0.2), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

Посмотреть таблицу

План	Базис	В	x 1	x 2	x 3	x 4	x 5	x 6	min
2	x 2	5500	0.5	1	2	5	0	0	11000
x 5	10	0.04	0	-0.02	-0.1	1	0	250
x 6	2500	2.5	0	0	-5	0	1	1000
Индексная строка	F(X2)	27500	-0.5	0	6	25	0	0	0

Итерация №1
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x₁, так как наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления и из них выберем наименьшее:
Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен 0.04 и находится на пересечении ведущего столбца и ведущей строки. Формируем следующую часть симплексной таблицы. Вместо переменной x в план 2 войдет переменная x₁. Строка, соответствующая переменной x₁ в плане 2, получена в результате деления всех элементов строки x₅ плана 1 на разрешающий элемент РЭ=0.04. На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x₁ плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x₁ и столбец x₁.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:

Посмотреть таблицу
Конец итераций: найден оптимальный план. Окончательный вариант симплекс-таблицы:

План	Базис	В	x 1	x 2	x 3	x 4	x 5	x 6	min
3	x 2	5375	0	1	2.25	6.25	-12.5	0	11000
x 1	250	1	0	-0.5	-2.5	25	0	250
x 6	1875	0	0	1.25	1.25	-62.5	1	1000
Индексная строка	F(X3)	27625	0	0	5.75	23.75	12.5	0	0

Оптимальный план можно записать так: x2 = 5375, x1 = 250, x6 = 1875; F(X) = 3*250 + 5*5375 = 27625

Решение двойственной задачи дает оптимальную систему оценок ресурсов.
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Из теоремы двойственности следует, что Y = C*A -1 .
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных x₄ , x₅ , x₆ .
Тогда Y = C*A -1 =
Оптимальный план двойственной задачи равен: y₁ = 23.75, y₂ = 12.5, y₃ = 0
Z(Y) = 1100*23.75+120*12.5+8000*0 = 27625
Подставим оптимальный план прямой задачи в систему ограниченной математической модели:
0.1*250 + 0.2*5375 + 0.4*0 = 1100 = 1100
0.05*250 + 0.02*5375 + 0.02*0 = 120 = 120
3*250 + 1*5375 + 2*0 = 6125 0).
2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y₃ = 0.
Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов.
При постановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:
0.1*23.75 + 0.05*12.5 + 3*0 = 3 = 3
0.2*23.75 + 0.02*12.5 + 1*0 = 5 = 5
0.4*23.75 + 0.02*12.5 + 2*0 = 9.75 > 4
1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₁>0).
2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x₃ = 0.
Величина двойственной оценки показывает, на сколько возрастает значение целевой функции при увеличении дефицитного ресурса на единицу.
Например, увеличении 1-го ресурса на 1 приведет к получению нового оптимального плана, в котором целевая функция возрастает на 23.75 и станет равной: F(x) = 27625 + 23.75 = 27648.75
Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции.
Пусть каждое значение параметра целевой функции изменится на ∆ с_i. Найдем интервалы, при которых будет экономически выгодно использование ресурсов.
1-ый параметр целевой функции может изменяться в пределах:

-3.8 ≤ с₁ ≤ 1
Таким образом, 1-параметр может быть уменьшен на 3.8 или увеличен на 1
Интервал изменения равен: [3-3.8; 3+1] = [-0.8;4]
Если значение c₁ будет лежать в данном интервале, то оптимальный план не изменится.

2-ый параметр целевой функции может изменяться в пределах:

-0.5 ≤ с₂ ≤ 9.5
Таким образом, 2-параметр может быть уменьшен на 0.5 или увеличен на 9.5
Интервал изменения равен: [5-0.5; 5+9.5] = [4.5;14.5]
Если значение c₂ будет лежать в данном интервале, то оптимальный план не изменится.

Проведем анализ устойчивости двойственных оценок.
1-ый запас может изменяться в пределах:

-860 ≤ b₁ ≤ 100
Таким образом, 1-ый запас может быть уменьшен на 860 или увеличен на 100
Интервал изменения равен: [1100-860; 1100+100] = [240;1200]
2-ый запас может изменяться в пределах:

-10 ≤ b₂ ≤ 30
Таким образом, 2-ый запас может быть уменьшен на 10 или увеличен на 30
Интервал изменения равен: [120-10; 120+30] = [110;150]
Составим субоптимальные варианты плана с учетом изменений исходных данных модели (таблицы).
Пусть 2-ый ресурс увеличили на 50

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (50)	Расчет варианта плана
x 2	5375	6.25	312.5	5687.5
x 1	250	-2.5	-125	125
x 6	1875	1.25	62.5	1937.5
F(X)	27625	23.75	1187.5	28812.5

Пусть 1-ый ресурс уменьшили на -5

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (-5)	Расчет варианта плана
x 2	5375	-12.5	62.5	5437.5
x 1	250	25	-125	125
x 6	1875	-62.5	312.5	2187.5
F(X)	27625	12.5	-62.5	27562.5

Задание : Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по решению каждой из них найти решение другой. Одну из задач решить графическим методом.
F(X) = 3x₁ + x₂ → min
— 2x₁ + x₂≥4
2x₁ + x₂≤8
3x₁ + 2x₂≥6
Решение.
I этап. Приводим систему к каноническому виду.
II этап. Решаем симплекс-методом.
Примечание: Если задача решается данным калькулятором, то предыдущие два этапа пропускаем, поскольку они автоматически включены в решение.
На втором этапе окончательный вариант симплекс-таблицы имеет вид:

Базис	B	x1	x2	x3	x4	x5	x6	x7
x5	2	-7	0	-2	0	1	2	-1
x4	4	4	0	1	1	0	-1	0
x2	4	-2	1	-1	0	0	1	0
F(X3)	4	-5	0	-1	0	0	1-M	-M

Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Записываем оптимальный план:
x₁ = 0, x₂ = 4, F(X) = 1•4 = 4

Составим двойственную задачу к прямой задаче.
— 2y₁ + 2y₂ + 3y₃≤3
y₁ + y₂ + 2y₃≤1
4y₁ + 8y₂ + 6y₃ → max
y₁ ≥ 0, y₂ ≤ 0, y₃ ≥ 0
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из теоремы двойственности следует, что Y = C*A -1 . Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

A = (A5, A4, A2) =

Определяем обратную матрицу D = А -1 через алгебраические дополнения:

D = A -1 =

Обратите внимание, обратная матрица A -1 расположена в столбцах дополнительных переменных окончательного варианта симплекс-таблицы. Тогда Y = C*A -1 =

(0, 0, 1) x

= (1;0;0)

Примечание: см. как умножать матрицы.
Оптимальный план двойственной задачи равен (двойственные оценки): y₁ = 1, y₂ = 0, y₃ = 0, Z(Y) = 4*1+8*0+6*0 = 4

Двойственные оценки определяют дефицитность используемых ресурсов и показывают, насколько возрастает максимальное значение целевой функции прямой задачи при увеличении количества соответствующего ресурса на единицу.

Проверим критерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y), то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно.
Связь прямой и двойственной задач состоит, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.
Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей оценки продукции и ресурсов, и обуславливают убыточность всякого другого плана, отличного от оптимального. В данном примере двойственная оценка (теневая или альтернативная) y₁ больше всех, что означает ценность ресурса №1.

Пример №2 . Для выполнения задания необходимо, чтобы одновременно взлетели 50 АК I-го вида, 30 АК 2-го вида и 45 АК 3-го вида. АК расположены на аэродромах I и II. В таблице представлено среднее время взлета (в секундах) с соответствующего аэродрома одного АК данного типа.

Номер аэродрома	Тип АК
	1	2	3
I	4	10	10
II	6	8	20

Как следует разместить АК по аэродромам, чтобы время последовательного взлета всего наряда АК было минимальным? До какой степени можно изменить время взлета каждого АК, чтобы при этом оптимальное решение осталось прежним.

Решение. Обозначим через:
x₁₁ – АК 1-го типа на первом аэродроме,
x₁₂ – АК 1-го типа на втором аэродроме,
x₂₁ – АК 2-го типа на первом аэродроме,
x₂₂ – АК 2-го типа на втором аэродроме,
x₃₁ – АК 3-го типа на первом аэродроме,
x₃₂ – АК 3-го типа на втором аэродроме,

После найденного решения, ответом на первый вопрос будут значения переменных x₁₁, x₁₂, x₂₁, x₂₂, x₃₁,x₃₂. Информация об ответе на второй вопрос будет расположена в разделе Интервалы устойчивости коэффициентов целевой функции .

Источник