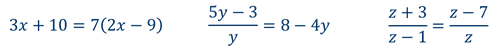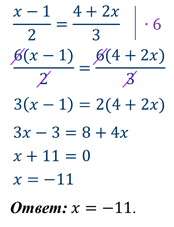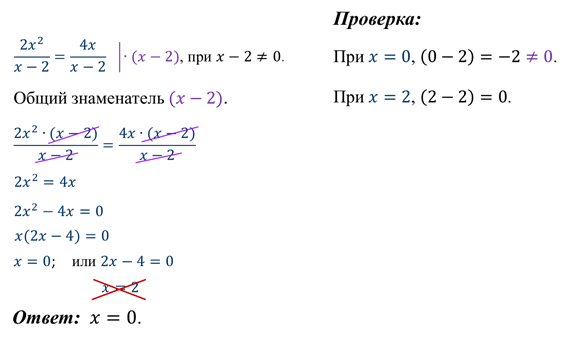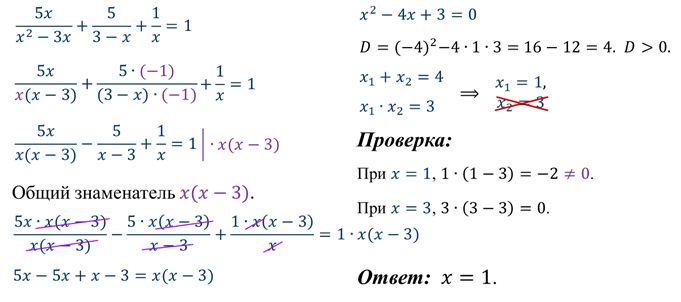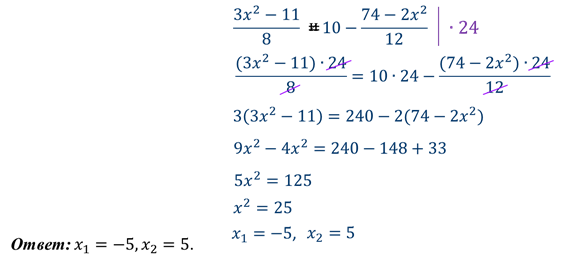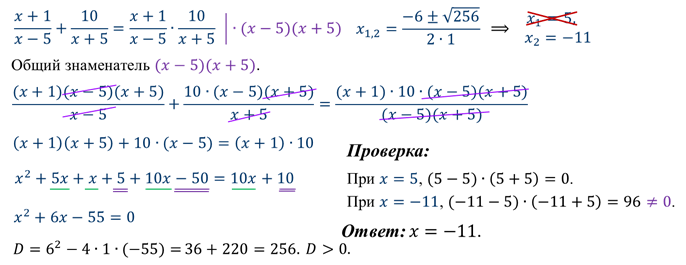Способы решения дробно рациональных уравнений 8 класс

Решение дробных рациональных уравнений. 8 класс
методическая разработка по алгебре (8 класс) по теме

Первый урок по теме: Решение дробных рациональных уравнений. Вспоминаются уже известные способы при решении дробных уравнений, рассматриваются новые способы

Скачать:

Вложение	Размер
Презентация	97.5 КБ
Урок по теме: Решение дробных рациональных уравнений	74.5 КБ

Предварительный просмотр:

Подписи к слайдам:

Решение дробных рациональных уравнений Алгебра 8 класс

7 х – 14 = 0 Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробными рациональными уравнениями. 1) 2) 3) 4) 5) 6) 7)

Алгоритм решения дробных рациональных уравнений Найти общий знаменатель дробей, входящих в уравнение. Умножить обе части уравнения на общий знаменатель, не забыв написать ОДЗ. Решить получившееся целое уравнение. Исключить из его корней те, которые обращают в нуль общий знаменатель (используя ОДЗ или проверкой). Записать ответ.

Алгоритм решения дробных рациональных уравнений Перенести все в левую часть. Привести дроби к общему знаменателю. Решить уравнение, используя правило: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. Исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой) Записать ответ.

Предварительный просмотр:

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

• закрепление понятия дробного рационального уравнения;
• рассмотреть различные способы решения дробных рациональных уравнений;
• рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
• обучить решению дробных рациональных уравнений по алгоритму.

• развитие умения правильно оперировать полученными знаниями, логически мыслить;
• развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
• развитие критического мышления;
• развитие навыков исследовательской работы.

• воспитание познавательного интереса к предмету;
• воспитание самостоятельности при решении учебных задач;
• воспитание воли и упорства для достижения конечных результатов.

Тип урока : урок – закрепление и систематизация знаний, умений и навыков.

1. Организационный момент.

Здравствуйте, ребята! Сегодня на уроке мы рассмотрим с вами различные способы решения дробных рациональных уравнений. На доске написаны уравнения, посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом, решение уравнений

Ответьте, пожалуйста, на следующие вопросы:

1. Как называется уравнение №1? ( Линейное .) Способ решения линейных уравнений. ( Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель ).

Решим уравнение №1

1. Как называется уравнение №3? ( Квадратное. ) Способы решения квадратных уравнений. ( Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия .)

Решим уравнение №3

1. Что представляет собой уравнение №2? ( Пропорцию ). Что такое пропорция? ( Равенство двух отношений .) Основное свойство пропорции. ( Если пропорция верна, то произведение ее крайних членов равно произведению средних членов .)

Решим уравнение №2

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5). Но так как данное уравнение имеет знаменатель, содержащий неизвестное, то необходимо написать …? ОДЗ.

( х – 2)( х – 4) = ( х + 2)( х + 3)

х 2 – 4 х – 2 х + 8 = х 2 + 3 х + 2 х + 6

х 2 – 6 х – х 2 – 5 х = 6 – 8

1. Решим уравнение №4. Какие свойство используются при решении этого уравнения? ( Если обе части уравнения умножить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному .)

3 х – 3 + 4 х = 5х

Какое дробно-рациональное уравнение можно решить, умножая обе части уравнения на знаменатель? (№6).

х 2 – 7 х + 12 = 0

D = 1 > 0, х 1 = 3, х 2 = 4.

1. Теперь решим уравнение №7 двумя способами.

Когда дробь равна нулю? ( Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю .)

х ² − 3 х + х – 5 – х – 5 = 0

D = 49 > 0, х 1 = 5, х 2 = − 2

х = 5 не удовлетворяет ОДЗ. Говорят, 5 – посторонний корень.

| ∙ х ( х – 5) ОДЗ: х ≠ 0, х ≠ 5

х ( х – 3) + х – 5 = х + 5

х ² − 3 х + х – 5 – х – 5 = 0

D = 49 > 0, х 1 = 5, х 2 = − 2

х = 5 не удовлетворяет ОДЗ. 5 – посторонний корень.

Давайте попробуем сформулировать алгоритм решения дробных рациональных уравнений данным способом. Дети сами формулируют алгоритм.

Алгоритм решения дробных рациональных уравнений:

1. Перенести все в левую часть.
2. Привести дроби к общему знаменателю.
3. Решить уравнение, используя правило: дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
4. Исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)
5. Записать ответ.

Другой способ решения.

Алгоритм решения дробных рациональных уравнений:

1. Найти общий знаменатель дробей, входящих в уравнение;

2. Умножить обе части уравнения на общий знаменатель; не забыв написать ОДЗ

3. Решить получившееся целое уравнение;

4. Исключить из его корней те, которые обращают в нуль общий знаменатель (используя ОДЗ или проверкой)

5. Записать ответ.

Также можно решить уравнение, используя основное свойство пропорции, не забыв исключить из его корней те, которые обращают знаменатель в нуль (с помощью ОДЗ или проверкой)

8. Подведение итогов урока.

Итак, сегодня на уроке мы с вами познакомились с дробными рациональными уравнениями, научились решать эти уравнения различными способами. На следующем уроке, дома у вас будет возможность закрепить полученные знания.

Какой метод решения дробных рациональных уравнений, по вашему мнению, является более легким, доступным, рациональным? Не зависимо от метода решения дробных рациональных уравнений, о чем необходимо не забывать? В чем «коварство» дробных рациональных уравнений?

Источник

Урок по теме «Решение дробных рациональных уравнений». 8-й класс

Разделы: Математика

Класс: 8

Цели урока:

• формирование понятия дробных рационального уравнения;
• рассмотреть различные способы решения дробных рациональных уравнений;
• рассмотреть алгоритм решения дробных рациональных уравнений, включающий условие равенства дроби нулю;
• обучить решению дробных рациональных уравнений по алгоритму;
• проверка уровня усвоения темы путем проведения тестовой работы.

• развитие умения правильно оперировать полученными знаниями, логически мыслить;
• развитие интеллектуальных умений и мыслительных операций — анализ, синтез, сравнение и обобщение;
• развитие инициативы, умения принимать решения, не останавливаться на достигнутом;
• развитие критического мышления;
• развитие навыков исследовательской работы.

• воспитание познавательного интереса к предмету;
• воспитание самостоятельности при решении учебных задач;
• воспитание воли и упорства для достижения конечных результатов.

Тип урока: урок – объяснение нового материала.

Ход урока

1. Организационный момент.

Здравствуйте, ребята! На доске написаны уравнения посмотрите на них внимательно. Все ли из этих уравнений вы сможете решить? Какие нет и почему?

Уравнения, в которых левая и правя часть, являются дробно-рациональными выражениями, называются дробные рациональные уравнения. Как вы думаете, что мы будем изучать сегодня на уроке? Сформулируйте тему урока. Итак, открываем тетради и записываем тему урока «Решение дробных рациональных уравнений».

2. Актуализация знаний. Фронтальный опрос, устная работа с классом.

А сейчас мы повторим основной теоретический материл, который понадобиться нам для изучения новой темы. Ответьте, пожалуйста, на следующие вопросы:

1. Что такое уравнение? (Равенство с переменной или переменными.)
2. Как называется уравнение №1? (Линейное.) Способ решения линейных уравнений. (Все с неизвестным перенести в левую часть уравнения, все числа — в правую. Привести подобные слагаемые. Найти неизвестный множитель).
3. Как называется уравнение №3? (Квадратное.) Способы решения квадратных уравнений. (Выделение полного квадрата, по формулам, используя теорему Виета и ее следствия.)
4. Что такое пропорция? (Равенство двух отношений.) Основное свойство пропорции. (Если пропорция верна, то произведение ее крайних членов равно произведению средних членов.)
5. Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.)
6. Когда дробь равна нулю? (Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.)

3. Объяснение нового материала.

Решить в тетрадях и на доске уравнение №2.

Какое дробно-рациональное уравнение можно попробовать решить, используя основное свойство пропорции? (№5).

х 2 -4х-2х+8 = х 2 +3х+2х+6

х 2 -6х-х 2 -5х = 6-8

Решить в тетрадях и на доске уравнение №4.

Какое дробно-рациональное уравнение можно попробовать решить, умножая обе части уравнения на знаменатель? (№6).

Теперь попытайтесь решить уравнение №7 одним из способов.

Источник

Решение дробных рациональных уравнений

Урок 24. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение дробных рациональных уравнений»

Для начала давайте вспомним определения целых, дробных и рациональных выражений.

Итак, целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Целые и дробные выражения называют рациональными. Вообще, рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

До этого мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований сводилось к линейному уравнению. Теперь же наши возможности стали гораздо шире: мы можем решить рациональное уравнение, которое сводится и к квадратному уравнению.

Давайте рассмотрим уравнения:

Заметим, что во всех этих уравнениях левая и правая части являются рациональными выражениями. Такие уравнения называют рациональными уравнениями.

Рациональное уравнение, в котором и левая и правая части являются целыми выражениями, называют целым.

Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным.

Возвращаясь к нашим уравнениям, видим, что первое уравнение является целым, а второе и третье – дробными рациональными.

Пример 1. Решить уравнение.

Пример 2. Решить уравнение.

Если среди найденных корней окажется такое число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения быть не может, его называют посторонним корнем и в ответ не включают.

Пример 3. Решить уравнение.

Запишем алгоритм решения дробно рациональных уравнений. Чтобы решить дробно рациональное уравнение, надо:

1) Разложить все знаменатели дробей, входящих в уравнение, на множители.

2) Найти общий знаменатель этих дробей.

3) Умножить все слагаемые данного уравнения на общий знаменатель.

4) Решить получившееся целое уравнение.

5) Из найденных корней исключить те, которые обращают в нуль общий знаменатель данного уравнения.

Задание 1: при каких значениях х равны значения выражений?

Задание 2: найти значение переменной х, при котором сумма дробей равна их произведению.

Уравнения, в которых в левой и правой частях записаны рациональные выражения, называют рациональными уравнениями.

Рациональное уравнение, в котором и левая и правая части являются целыми выражениями, называют целым.

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называют дробным.

Чтобы решить дробно рациональное уравнение, надо:

1. Разложить все знаменатели дробей, входящих в уравнение, на множители.

2. Найти общий знаменатель этих дробей.

3. Умножить все слагаемые данного уравнения на общий знаменатель.

4. Решить получившееся целое уравнение.

Из найденных корней исключить те, которые обращают в нуль общий знаменатель данного уравнения.

Источник