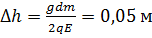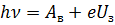Решение задач по физике, ЕГЭ – часть С
Примеры решений заданий части C ЕГЭ по физике.
С1. Дно водоёма всегда кажется расположенным ближе к поверхностиводы для наблюдателя, находящегося в лодке. Объяснить это явление.
Ответ:
Образец возможного решения
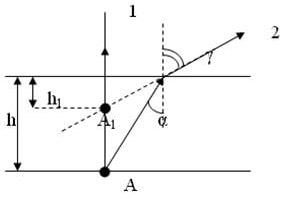
Рассмотрим ход лучей 1 и 2, отражённых от некоторой точки А, лежащей на дне водоёма. Луч 1 (взятый для удобства построения) падает перпендикулярно на границу раздела сред (вода-воздух) и не преломляется. Произвольный луч 2 падает на границу раздела под некоторым углом α и преломляется под углом γ (α h 1 меньше глубины водоёма h .
С2. Шар массой 1 кг свободно, без начальной скорости, падает с высоты 13,2 м. На высоте 10 м он насквозь простреливается горизонтально летящей пулей массой 10 г. Скорость пули за время движения в шаре изменяется от V 1=700 м/с до V2=100 м/с. Найдите кинетическуюэнергию шара в момент удара о горизонтальную поверхность земли.
Ответ:
Образец возможного решения
Кинетическая энергия шара в момент его падения на землю определяется следующим образом: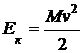 
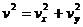
, где скорость шара v направлена под углом к горизонту, поскольку кроме вертикальной составляющей имеется еще и горизонтальная составляющая из-за взаимодействия с пулей.
;
Вертикальную составляющую скорости определяем из закона сохранения полной механической энергии: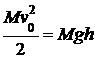 
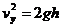
( h =13,2 м);
(поскольку пуля летела горизонтально, то взаимодействие с ней шара не скажется на вертикальной компоненте скорости);
Горизонтальную составляющую скорости шара определяем из закона сохранения импульса:
.
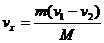
С3. Как изменится температура идеального газа, если увеличить его объем в 2 разапри осуществлении процесса, описываемого формулой pV 4 = const ?
Ответ:
Образец возможного решения
Выразим из уравнения Менделеева-Клапейрона давление p:
(1).
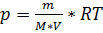
Подставим (1) в формулу, описывающую данный процесс:
; Следовательно, при увеличении объема в 2 раза температура должна понизиться в 8 раз
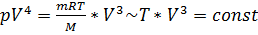
С4. Электрическое поле образовано двумя неподвижными, вертикальнорасположенными, параллельными, разноименно заряженными непроводящимипластинами. Пластины распложены на расстоянии d = 5см друг от друга. Напряженность поля между пластинами Е =10 4 В/м. Между пластинами, на равном расстоянии от них, помещен шарикс зарядом q = 10 -5 Кл и массой m = 20г. После того как шарикотпустили, он начинает падать и ударяется об одну из пластин. На какоерасстояние Δ h по вертикалисместится шарик к моменту его удара об одну из пластин?
Ответ:
Образец возможного решения
Движение шарика можно «разложить» на равноускоренное движение по вертикали под действием силы тяжести и на равноускоренное движение по горизонтали под действием силы Кулона. За одно и то же время t шарик проходит путь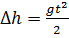 
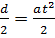
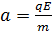
(по вертикали) и 
(по горизонтали). Ускорение a находим по второму закону Ньютона: 
.
Таким образом, 
С5. Маленький шарик массой 1 г, несущий заряд 0,15 мкКл, брошен издалека соскоростью 1 м/с в сферу, имеющую заряд 0,3 мкКл. При каком минимальном значениирадиуса сферы шарик достигнет ее поверхности?
Ответ:
Образец возможного решения
В момент бросания шарик обладает кинетической энергией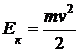 
, а его потенциальная энергия в электростатическом поле заряженной сферы равна нулю.
В тот момент, когда шарик достигнет поверхности сферы, его потенциальная энергия равна
, а кинетическая энергия равна нулю (из условия минимального значения радиуса сферы).
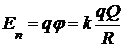
Применяя закон сохранения энергии, получаем
. Отсюда 
=0,81 (м)
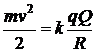
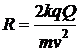
С6. В вакууме находятся два покрытых кальцием электрода, к которым подключенконденсатор ёмкостью С. При длительном освещении катода светом с длиной волны λ=100нм фототок, возникший вначале, прекращается, а на конденсаторе появляется заряд q =9,6∙10 -10 Кл.Работа выхода электрона из кальция А=4,42∙10 -19 Дж. Определитеёмкость конденсатора С.
Ответ:
Образец возможного решения
Напряжение на конденсаторе U будет равно задерживающей разности потенциалов Uз, которое можно найти из уравнения Эйнштейна для фотоэффекта: 
Отсюда: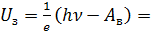 
9,6 В.
Находим емкость конденсатора: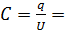 
100 пФ.
Главная » Подготовка к ЕГЭ по физике » Решение задач по физике, ЕГЭ – часть С
Источник
Методика решения задач по физике ЕГЭ части С (механика)
материал для подготовки к егэ (гиа) на тему
Данный материал может быть использоан учителями физики для подготовке к ЕГЭ.
Скачать:
| Вложение | Размер |
|---|---|
| Методика решения задач по физике части С | 2.11 МБ |
Предварительный просмотр:
Подписи к слайдам:
Перед ребенком, решившим выбрать в своей жизни дорогу научно-технического направления, встают две задачи: ЭКЗАМЕНЫ (ГИА и ЕГЭ) . И для сдачи экзаменов в новых форматах успешной учебы в течение всех прошедших лет оказывается недостаточно. Проблема в том, что сдача экзаменов требует от ребенка особого алгоритма работы, повышенной интенсивности мыслительной деятельности, работы в измененном психофизическом стрессовом состоянии и работы с большим объемом информации. Можно уверенно сказать, что школьная программа на это не рассчитана.
1. Поэтапно, в соответствии с последовательностью изучения 6 разделов школьного курса физики освоить все содержание основной триады (понятия-законы-границы применимости). Более того, в задачи школьной программы вовсе, не входит подготовка к ГИА и ЕГЭ. По действующему законодательству в задачи школы входит освоение учениками федеральных государственных образовательных стандартов (ФГОС) и не более. А экзамены ГИА и ЕГЭ – это уже проверка государством уровня подготовленности учеников по своим стандартам, которые попросту не связаны с ФГОС.
2. После изучения триады соответствующего раздела физики освоить методы решения физических задач из этого раздела. 3. Проконтролировать освоение изученного раздела. «Подводные камни» Методика работает только при полной мотивации ребенка на обучение. Уговоры и принуждения при таком подходе попросту «не сработают». Школьнику необходимо выделить время на заучивание триады (понятия-законы-границы применимости), этого за него никто сделать не сможет. В случае же, если необходимые составляющие заучены не будут, все остальные учебные действия потеряют свою базовую опору и в сознании школьника не сохранятся.
Существенные затруднения у учащихся ежегодно возникают при решении качественных задач. Порядка 70-75% экзаменуемых получали за ее решение ноль баллов. Дело в том, что примеры качественных заданий в пособиях для подготовки к экзамену и в опубликованном открытом сегменте КИМ присутствуют в минимальном количестве. Таким образом, возможности абитуриентов по целенаправленной подготовке к выполнению этой части экзаменационной работы были ограничены.. Результаты экзамены показали, что обучающиеся не умеют корректно использовать физические термины, ссылаясь при необходимости на физические законы.
В качестве примера приведем подробное решение следующей задачи. Задача С1. Доказать, что крупные капли дождя падают быстрее, чем мелкие. Капли имеют форму шара, силу сопротивления воздуха считать пропорциональной площади поперечного сечения капли. Решение: Прежде всего, следует понять модель процесса. Совершенно ясно, что в данной задаче нельзя пренебречь силой сопротивления воздуха. Именно она и оказывает решающее влияние на скорость капли, и дело здесь не только в разной массе капель воды. Рассмотри силы, действующие на каплю при ее падении в воздухе
На каплю вверх действует сила сопротивлении воздуха. пропорциональная квадрату радиуса (площади поперечного сечения), а вниз действует сила тяжести , пропорциональная массе тела, а следовательно объему тела, т.е. кубу радиуса капли. Таким образом, с ростом размера капли сила тяжести растет быстрее силы сопротивления воздуха., равнодействующая этих сил (направленная вниз) растет и растет ускорение капли. F т F сопр
Основное затруднение при решении задач это создание алгоритма. К сожалению создать такой алгоритма невозможно. В некоторых разделах физики например в динамике некоторые элементы таких алгоритмов можно придумать. В динамике очень важно находить все силы. Действующие на тело и ускорение. Что является первичным в механике? Первичным является взаимодействие: гравитационное, электромагнитное, сильное и слабое. Результатом взаимодействия является сила. Определение сил и является построением модели задачи.
Задача С2. Груз массой m располагается на поверхности клина с углом при основании α. К грузу прикреплена нить, другой конец которой привязан к гвоздю. Вбитому в вершину клина. Клин перемещается в горизонтальном направлении с ускорением а .Найти силу натяжения нити T силу давления груза на поверхность клина F д. Решение. На клин действует сила, вынуждающая его двигаться с ускорением а в горизонтальном направлении. Эта сила приложена именно к клину, но не к грузу на нем. Груз хоть и движется вместе с клином с таким же ускорением а , но под действием иных сил, приложенных к нему. Этими силами являются сила тяжести mg , сила натяжения нити Т и сила реакции опоры N . Совместное действие этих трех сил и сообщает грузу ускорение а .
Y X N mg T cos α N sin α T N cos α T sin α α α α α α a
Согласно второму закону Ньютона, применительно к грузу: ma = mg + T + N Запишем закон в скалярном виде. Спроецируем эти силы на оси координат ОХ и OY , сонаправив ось ОХ с ускорением груза и клин а . Тогда второй закон Ньютона в проекциях применительно к движению груза на клине имеет вид: ma = 0 + T cos α – N sin α ( 1 ) В этом уравнение есть две искомые величины N и T . Для их определения составим еще одно уравнение, спроецировав силы, приложенные к грузу , на ось OY : mg =T sin α +N cos α ( 2 ) Из уравнения ( 2 ) выразим силу N : N = (mg -T sin α ) / cos α ( 3 )
и подставим в уравнение ( 1 ): ma = T cos α – (mg -T sin α ) sin α cos α преобразуем : ma cos α = T cos 2 α — mg sin α +T sin 2 α m (a cos α + g sin α ) = T ( sin 2 α + cos 2 α ) sin 2 α + cos 2 α = 1 отсюда: T = m (a cos α + g sin α ) – первая величина найдена. По третьему закону Ньютона сила давления груза F давл равна силе давления клина на груз, т.е. силе реакции опоры N , которая равна ( 3 ): N = (mg -T sin α ) / cos α – вторая величина найдена, Задача решена.
Задача С3 . Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля, летящая навстречу шару. Она пробивает его и продолжает двигаться горизонтально. После попадания пули в шар он продолжает движение в прежнем направлении, пока нить не составит с вертикалью угол 39°. Определите массу пули, если в результате попадания в шар скорость пули уменьшилась на 100 м/с. (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити, с os 39 ° = 0,778.
1. По закону сохранения импульса Mu 1 — m υ 1 = Mu 2 — m υ 2 , где m – масса пули, u 1 , u 2 – скорости шара до и после взаимодействия с пулей соответственно. Отсюда ∆ υ = υ 2 — υ 1 = ( u 2 — u 1 ) ( 1 ) 2. По закону сохранения энергии скорость шара в нижней точке траектории до попадания в него пули равна: u 1 = √ 2gl(1- cosa ) . 3. По закону сохранения энергии скорость шара в нижней точке траектории после вылета из него пули равна: u 2 = √ 2gl(1- cos β ) . m M
4. Подставляя в формулу ( 1 ) изменение скорости шара, получим: ∆ υ = υ 2 — υ 1 = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) , откуда: m = M √ 2gl(1- cos β ) — √ 2gl(1- cosa ) 5. Проводя вычисления, получим: m = 1 √ 2 . 10 . 0,9 (1 – 0,778) — √ 2 . 10 . 0,9 ( 1 – 0,5) = 0,01 кг Ответ: 0,01 кг υ 2 — υ 1 m — 100
ЕЕЕЕЕЕ Е k Задача 4. Е k Е k Е P Задача решена.
Задача 5. Тело массой m связано двумя пружинами одинаковой жесткости k , которые один раз соединяются параллельно, а второй- последовательно. В обеих случаях телу сообщается скорость υ . В каком отношении будут находится амплитуды колебаний грузов без учета трения и сопротивления ?
Решение: 1. В первом случае пружины соединены параллельно, поэтому общая их жесткость равна k 1 = k + k = 2k . Закон сохранения энергии представится следующим образом: 2. При последовательном соединении пружин: 3.Отношение амплитуд собственных колебаний: Задача решена.
Задача С6. Небольшой шар, надет на гладкую горизонтальную спицу, прикреплен к двум невесомым пружинам, вторые концы которых заделаны в неподвижную стену так, что в положении равновесия пружины не деформированы. Найти период колебаний тела, если при ее поочередном подвешивании к пружинам их удлинение составило ∆ x 1 и ∆ x 2 .
Решение. 1. Жесткости пружин: 2. Пружины соединены параллельно. Поэтому их общая жесткость равна сумме жесткостей:
3. Период колебания тела: Задача решена.
Задача 6. Поднимая при помощи подвижного блока ведро с песком весом 200 Н на высоту 5 м, производят работу 1020 Дж. Какой процент составляет энергия, которая была затрачена непроизводительно? Решение: Полезная работа, которую нужно совершить, чтобы поднять груз весом Р на высоту h равна: А= Р . h = 200 . 5 = 1000 Дж . Общая совершенная работа составила А общ =1020 Дж. Таким образом, непроизводительно была затрачена энергия: ∆ А =А общ – А = 1020 — 1000 = 20 Дж. Эта величина составляет в процентном отношении: (∆ А /А общ ) . 100%= (20/100) . 100% = 2% То есть непроизводительно было затрачено 2% от общей энергии Задача решена.
По теме: методические разработки, презентации и конспекты
«Использование математических методов для решения практических задач по физике и электротехнике»
Математика для Ньютона была главным орудием в физических изысканиях; он подчеркивал, что понятия математики заимствуются извне и возникают как абстракция явлений и процессов физического мира, что по с.
Методическая разработка по решению задач по физике
В помощь учащимся создана методическая разработкарешения задач по теме «Механическая работа, мощность.».
Проект учебного занятия по теме: Методика обучения решению задач на нахождение дроби от числа.
Подробный проект учебного занятия по теме «Методика обучения решению задач на нахождение дроби от числа» поможет преподавателям СПО качественно подготовится к его проведению. Данное занятие проводится.
Методическое пособие к решению задач по дисциплине «Техническая механика»
Методическое пособие к решению задач предназначено для студентов строительных специальностей всех форм обучения, как вспомогательное пособие при выполнении ими самостоятельных работ и для .
Разработка по физике «АЛГОРИТМИЗАЦИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ ПРИ РЕШЕНИИ ЗАДАЧ ПО ФИЗИКЕ»
Данная разработка ориентирована на преподавателя физики старших классов.
разработка «Алгоритмизация учебной деятельности при решении задач по физике»
Данная разработка расчитана на преподавателей техникума.
Методические рекомендации по решению задач по физике для 1 курса.
ОБРАТИТЕ ВНИМАНИЕКак решать задачи по кинематике * прямолинейного движения• При решении задач нужно уметь переходить от векторной записи уравнения движения к записи .
Источник
