Способы реализации моделей характеристика моделей

Способы реализации моделей

В случае, когда модели сознательно создаются человеком, в зависимости от того, каким образом и с помощью чего они создаются, различают следующие виды моделей.

1. Материальные, или вещественные модели, если при их создании используются средства окружающего мира.

2. Абстрактные, или идеальные модели, если при их создании используются средства сознания человека. По-другому, это идеальные конструкции, построенные посредством мышления.

Примерами материальных моделей могут служить манекены, протезы, масштабные копии сооружений, памятники, скульптуры, картины и т.п.

Примерами идеальных моделей могут служить уравнения, передаточные функции, частотные характеристики, матрицы, графы и другие математические модели, а также различные гипотезы и даже целые теории.

Материальные модели

Материальные модели создаются с помощью материи (средств окружающего мира). Такими моделями являются куклы, реалистические картины, скульптуры, чучела и т.п. Для того чтобы модель была отображением оригинала необходимо, чтобы между моделью и оригиналом было установлено отношение подобия.

Виды подобия

Теория подобия утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие обычно не требуется, однако модель должна достаточно хорошо отображать исследуемую сторону функционирования объекта.

Существуют различные способы задания отношения подобия.

П р я м о е п о д о б и е

Отношение прямого подобия устанавливается в результате физического взаимодействия в процессе создания модели (модель автомобиля, самолета, рис. 1.2 и 1.3).

Рис. 1.2. Модель автомобиля

При прямом виде подобия модель всегда внешне похожа на оригинал, и только при прямом подобии существует взаимозаменяемость модели и оригинала (например, копия живописной картины). Тем не менее, при этом виде подобия, даже в том случае, когда модель субстратна (изготовлена из тех же материалов, что и оригинал) возникает проблема при переносе результата моделирования с модели на оригинал.

Рис.1.3. Модель самолета

К о с в е н н о е п о д о б и е

Отношение косвенного подобия (аналогия) устанавливается не в результате физического взаимодействия, а объективно существует в природе и обнаруживается в форме совпадения абстрактных моделей, а затем используется в практике моделирования (например, электромеханические аналогии).

Рассмотрим пример, использующий электромеханическую аналогию.

Пример. Пусть механическая система состоит из пружины с жесткостью k, подвешенного на ней груза массой m и демпфера с коэффициентом вязкости b (рис. 1.4).

Рис.1.4. Механическая система, состоящая из пружины, груза и демпфера

В качестве входной переменной рассматривается вынуждающая сила F(t), а выходной переменной является расстояние до точки подвеса y(t). В этом случае вертикальные колебания груза можно описать уравнением:

где первое слагаемое в левой части уравнения соответствует второму закону Ньютона для движения тела массой m, второе слагаемое описывает действие демпфера, а третье – пружины.

В общем виде это линейное дифференциальное уравнение 2-го порядка можно записать:

Теперь рассмотрим электрическую систему, состоящую из источника ЭДС, являющейся внешним воздействием, активного сопротивления R, индуктивности L и емкости С (рис.1.5). Выходной переменной будем считать величину тока i(t).

Рис. 1.5. Электрическая система, состоящая из источника ЭДС, активного сопротивления, индуктивности и емкости

Согласно второму закону Ома сумма падений напряжений в цепи равна сумме ЭДС, поэтому уравнение, описывающее изменение тока в этой системе, будет иметь вид:

или, если продифференцировать по t и умножить на С обе части уравнения:

Обозначив LC=a₂, RC=a₁, 1= a₀, C=b₀, dE(t)/dt=x(t), получим:

Таким образом, при описании процесса, протекающего в электрической системе, мы получили линейное дифференциальное уравнение 2-го порядка, абсолютно идентичное тому, которое описывало процесс, протекающий в механической системе. Это и означает, что данные системы косвенно подобны.

У с л о в н о е п о д о б и е

Отношение условного подобия устанавливается в результате специального соглашения (условия). Этот вид подобия не является ни прямым, ни косвенным. Например, деньги как модель стоимости, паспорт как модель личности, сигнал как модель информации. Хотя условное подобие не требует физического сходства, но модели условного подобия должны строиться с учетом возможностей восприятия человека, поэтому выбор символики должен осуществляться очень тщательно, так, чтобы человек легко, быстро и уверенно распознавал символы.

Рис. 1.6. Деньги как пример модели условного подобия

Например, деньги являются моделью условного подобия стоимости любых товаров или услуг (рис. 1.6). Другим примером модели условного подобия может служить светофор, каждый из цветов которого предписывает по договоренности (условию) выполнение конкретного действия: красный – стоять, желтый – приготовиться к смене действия, зеленый – двигаться (рис.1.7).

Рис. 1.7. Светофор как пример модели условного подобия

Говорят, что наша жизнь полна условностей, следовательно, она полна моделей условного подобия. Приведите самостоятельно новые примеры таких моделей.

1.4.3. Идеальные модели

Идеальными, как уже упоминалось (п. 1.4), являются абстрактные модели, создаваемые с помощью человеческого сознания. К таковым относятся абстрактные рисунки и схемы, символы и знаки и, конечно же, естественные и специальные языки, которыми пользуются люди в профессиональном общении и в быту.

Модели, создаваемые средствами языка

Язык как средство общения может служить известным каждому человеку очевидным примером идеальной модели.

Различают уровни языков. Чем выше уровень языка, тем понятийно более емким он является, т.е. тем более лаконично можно выразить сложную мысль (сообщение). К языкам высокого уровня относят естественные языки (русский, английский и т.д.), а также профессиональные языки специальных наук, использующие много специфических терминов и предназначенные для общения специалистов. Дифференциация языков соответствует дифференциации наук, это приводит к созданию специальных языков более точных, чем естественные. Поэтому модели специальных наук содержат больше информации. Дальнейшая специализация научных дисциплин приводит к развитию и созданию дальнейшей иерархии языков.

К языкам более низкого уровня относят ограниченные языки, например, ограниченный естественный язык (ОЕЯ), используемый для диалогового общения человека с компьютером, уставный армейский язык, языки жестов, морские семафоры, алгоритмические языки и т.д.

Алгоритмические языки также в свою очередь различаются по уровню. Например, языки: С++, Фортран, Java – алгоритмические языки высокого уровня, а Ассемблер – низкого. Языки высокого уровня предъявляют минимальные требования к умению программировать, обладают концептуальной выразительностью, но являются менее гибкими и универсальными, чем языки низкого уровня. Языки низкого уровня напротив, трудоемки при составлении программ и требуют высокой квалификации программиста, но зато позволяют решать очень широкий класс задач, т.е. являются универсальными, а также гибкими с точки зрения многообразия описываемых проблем.

Естественный язык – это универсальное средство построения абстрактных моделей. Единицей языка является слово. Естественные языки отличает многозначность отдельных слов и словосочетаний, и это придает им свойство «размытости».

Универсальность и гибкость языка достигается за счет: 1) возможности введения в словарь новых слов; 2) возможности создания иерархических моделей по следующей схеме: слово – предложение – текст; понятие – отношение – определение – конструкция…

Итак, языковые модели обладают свойством неоднозначности. Например, слово «много» не означает именно сколько. Есть слова, имеющие различные значения (омонимы). С одной стороны, благодаря этому, любую ситуацию можно отобразить посредством языка с любой необходимой точностью. С другой стороны, это затрудняет реализацию процесса моделирования, поэтому обычно при языковом моделировании используют тезаурус.

Тезаурус (греч. thesaurus – сокровище, запас) представляет собой словарь, который освобожден от неоднозначности слов: в нем каждому слову может соответствовать только одно единственное понятие (в отличие от обычного словаря). Тезаурус образуется из фиксированного набора входящих понятий.

Для того чтобы состоялась передача полезной информации, заложенной в языковой модели, т.е. чтобы модель была воспринята, помимо передающей стороны, нужна приемная сторона, способная интерпретировать информацию. От того, как именно приемная сторона интерпретирует и использует полученную информацию, во многом зависят свойства данной языковой модели, в частности, такое свойство, как прагматика (см. ниже).

Знаковые модели

Существует ряд наук, в которых изучаются модели условного подобия, называемые сигналами: теория связи, информатика, теория управления, криптография и т.д.

Сигналы характеризуются различными параметрами: временем существования сигнала, шириной спектра, превышением мощности сигнала над мощностью помех и т.п. Правила построения и способы использования сигналов связаны с процессами кодирования и декодирования. Если модель используется человеком, то сигналы имеют специфику, связанную с органами его восприятия и носят названия «знаки». Исследованием знаковых моделей занимается наука семиотика. Семиотика включает следующие важные части.

1. Синтаксис задает правила, позволяющие отличать знаки друг от друга и строить знаковые конструкции (например, синтаксис русского языка);

2. Семантика задает отношения между знаками и смыслом, который в них первоначально заложен (буквально означает: обозначение);

3. Прагматика задает отношение между знаками и их пониманием воспринимающей стороной, т.е. теми, кто использует эти знаки в своей деятельности (буквально означает: действие).

Разумеется, что языковые модели близки к знаковым, а если принять слово за знак (сочетание символов-букв), то их можно рассматривать как разновидность знаковых моделей. В некоторых классификациях знаковые и языковые модели относят к общему виду символьных моделей (рис. 1.20). Однако огромное значение языков в жизни человека, их сложность и высокий уровень развития ставят языковые модели в особое положение, поэтому они и рассматриваются отдельно.

Пример. Дорожные знаки также представляют собой знаковые модели. Причем синтаксис в данном случае заключается в правилах начертания знаков: форме, цвете и размерах изображений, а также в материалах, используемых при изготовлении (светоотражающая краска) и т.п. Семантика каждого дорожного знака обозначена в Правилах дорожного движения (ПДД). Например, семантика знака, изображенного на рис. 1.8, заключается в смысле его названия: «Въезд запрещен».

Рис.1.8. Дорожный знак «Въезд запрещен»

Что же касается прагматики, то она зависит от пользователя: для обыкновенного дисциплинированного автолюбителя, работника дорожной службы и сотрудника ГИБДД, находящегося при исполнении служебных обязанностей, прагматика этого знака будет различной.

Существуют многочисленные аспекты исследования знаковых моделей, которые являются предметом таких наук, как: языкознание, информатика, криптография, графология, техническое черчение, нумизматика и т.д.

Источник

Понятие модели и моделирования

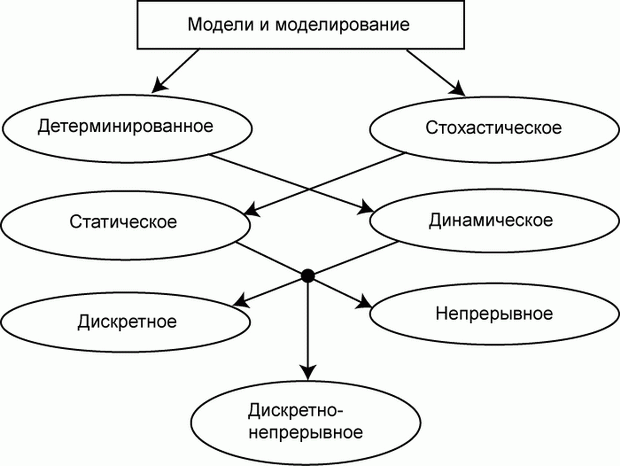
1.2.3. Классификация моделей и моделирования по признаку «способ реализации модели»

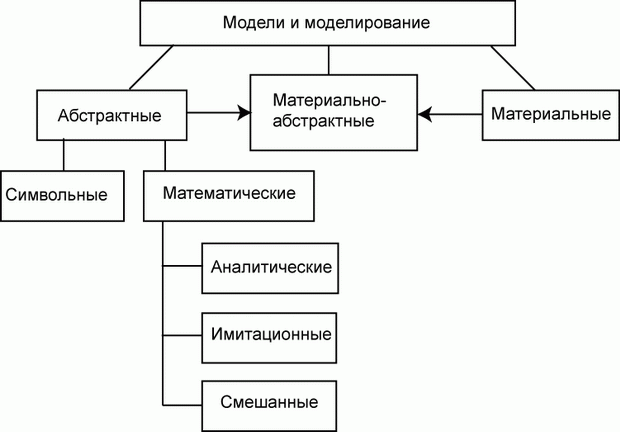
Согласно этому признаку модели делятся на два обширных класса:

• абстрактные (мысленные) модели;
• материальные модели.

Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.

Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.

Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:

Символическая модель — это логический объект, замещающий реальный процесс и выражающий основные свойства его отношений с помощью определенной системы знаков или символов. Это либо слова естественного языка, либо слова соответствующего тезауруса , графики, диаграммы и т. п.

Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.

Математическое моделирование — это процесс установления соответствия моделируемому объекту некоторой математической конструкции, называемой математической моделью, и исследование этой модели, позволяющее получить характеристики моделируемого объекта.

Математическое моделирование — главная цель и основное содержание изучаемой дисциплины.

Математические модели могут быть:

• аналитическими;
• имитационными;
• смешанными (аналитико-имитационными).

Аналитические модели — это функциональные соотношения: системы алгебраических, дифференциальных, интегро-дифференциальных уравнений, логических условий. Уравнения Максвелла — аналитическая модель электромагнитного поля. Закон Ома — модель электрической цепи.

Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик («в общем виде»). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.

Имитационное моделирование. Создание вычислительных машин обусловило развитие нового подкласса математических моделей — имитационных.

Имитационное моделирование предполагает представление модели в виде некоторого алгоритма — компьютерной программы, — выполнение которого имитирует последовательность смены состояний в системе и таким образом представляет собой поведение моделируемой системы.

Процесс создания и испытания таких моделей называется имитационным моделированием, а сам алгоритм — имитационной моделью.

В чем заключается отличие имитационных и аналитических моделей?

В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.

В случае же имитационного моделирования имитационная модель — программа — реализуется на ЭВМ.

Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.

Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.

Материальное моделирование основано на применении моделей, представляющих собой реальные технические конструкции. Это может быть сам объект или его элементы (натурное моделирование). Это может быть специальное устройство — модель, имеющая либо физическое, либо геометрическое подобие оригиналу. Это может быть устройство иной физической природы, чем оригинал, но процессы в котором описываются аналогичными математическими соотношениями. Это так называемое аналоговое моделирование. Такая аналогия наблюдается, например, между колебаниями антенны спутниковой связи под ветровой нагрузкой и колебанием электрического тока в специально подобранной электрической цепи.

Нередко создаются материально-абстрактные модели. Та часть операции, которая не поддается математическому описанию, моделируется материально, остальная — абстрактно. Таковы, например, командно-штабные учения, когда работа штабов представляет собой натурный эксперимент, а действия войск отображаются в документах.

Классификация по рассмотренному признаку — способу реализации модели — показана на рис. 1.2.

1.3. Этапы моделирования

Математическое моделирование как, впрочем, и любое другое, считается искусством и наукой. Известный специалист в области имитационного моделирования Роберт Шеннон так назвал свою широко известную в научном и инженерном мире книгу: » Имитационное моделирование — искусство и наука». Поэтому в инженерной практике нет формализованной инструкции, как создавать модели. И, тем не менее, анализ приемов, которые используют разработчики моделей, позволяет усмотреть достаточно прозрачную этапность моделирования.

Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.

Обычно целями моделирования являются:

• прогноз поведения объекта при новых режимах, сочетаниях факторов и т. п.;
• подбор сочетания и значений факторов, обеспечивающих оптимальное значение показателей эффективности процесса;
• анализ чувствительности системы на изменение тех или иных факторов;
• проверка различного рода гипотез о характеристиках случайных параметров исследуемого процесса;
• определение функциональных связей между поведением («реакцией») системы и влияющими факторами, что может способствовать прогнозу поведения или анализу чувствительности;
• уяснение сущности, лучшее понимание объекта исследования, а также формирование первых навыков для эксплуатации моделируемой или действующей системы.

Второй этап: построение концептуальной модели. Концептуальная модель (от лат. conception ) — модель на уровне определяющего замысла, который формируется при изучении моделируемого объекта. На этом этапе исследуется объект , устанавливаются необходимые упрощения и аппроксимации. Выявляются существенные аспекты, исключаются второстепенные. Устанавливаются единицы измерения и диапазоны изменения переменных модели. Если возможно, то концептуальная модель представляется в виде известных и хорошо разработанных систем: массового обслуживания, управления, авторегулирования, разного рода автоматов и т. д. Концептуальная модель полностью подводит итог изучению проектной документации или экспериментальному обследованию моделируемого объекта.

Результатом второго этапа является обобщенная схема модели, полностью подготовленная для математического описания — построения математической модели.

Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.

В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.

Результатом третьего этапа моделирования является программа , составленная на наиболее удобном для моделирования и исследования языке — универсальном или специальном.

Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.

Результат четвертого этапа — план эксперимента.

Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.

Шестой этап: обработка, анализ и интерпретация данных эксперимента. В соответствии с целью моделирования применяются разнообразные методы обработки: определение разного рода характеристик случайных величин и процессов, выполнение анализов — дисперсионного, регрессионного, факторного и др. Многие из этих методов входят в системы моделирования ( GPSS World, AnyLogic и др.) и могут применяться автоматически. Не исключено, что в ходе анализа полученных результатов модель может быть уточнена, дополнена или даже полностью пересмотрена.

После анализа результатов моделирования осуществляется их интерпретация , то есть перевод результатов в термины предметной области . Это необходимо, так как обычно специалист предметной области (тот, кому нужны результаты исследований) не обладает терминологией математики и моделирования и может выполнять свои задачи, оперируя лишь хорошо знакомыми ему понятиями.

На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.

Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.

Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.

В-третьих, результат каждого из этапов должен являться самоценным продуктом. Например, концептуальная модель может и не использоваться для дальнейшего преобразования в математическую модель, а являться описанием, хранящим информацию о системе, которое может использоваться как архив , в качестве средства обучения и т. д.

Источник