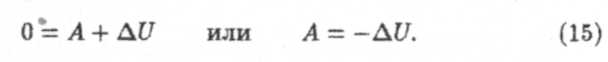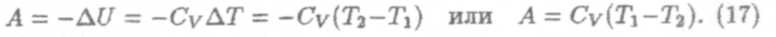Способы реализации адиабатического процесса

Адиабатический процесс

Адиабатическим называется процесс, происходящий без те­плообмена между системой и окружающей средой.

Осуществить адиабатический процесс в реальных условиях можно тремя способами.

1) Система должна иметь оболочку, теплопроводность которой равна нулю. Приближением к такой оболочке может служить сосуд Дьюара, т.е. сосуд с двойными посеребренным) стенками, из пространства между которыми выкачан воздух.

2) Процессы, протекающие очень быстро (расширение, ежа тие), при которых теплопередача не успевает произойти. На пример, накачивание велосипедной шины вызывает ее нагрева ние вследствие адиабатического сжатия.

3) Процессы, протекающие в очень больших объемах газа например, в атмосфере. Этот способ, строго говоря, сводите ко второму, так как расширение и сжатие происходит быстрее чем передача теплоты по всему объему.

В соответствии с первым началом термодинамики и с учетом что Q = 0, получаем

Из этой формулы видно, что при адиабатическом расширени! внутренняя энергия газа уменьшается, т.е. система совершае работу за счет своей внутренней энергии. А при адиабатиче ском сжатии внутренняя энергия системы увеличивается.

Адиабатический процесс в газе описывается уравнением Пуассона, которое имеет три фор­мы

Построим график уравнения (16а) (рис. 2). Полученная кривая (1) называется адиабатой. Сравнив адиабату с изотермой (2), мы уви­дим, что адиабата идет круче изо­термы.

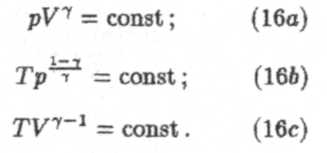
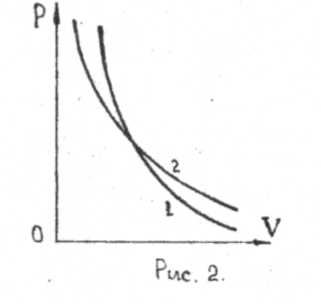
Это объясняется тем, что при изотермическом расширении давление газа уменьшается только за счет увеличения объема, а при адиабатическом расширении оно уменьшается и за счет увеличения объема и за счет повышения температуры.

В заключение получим работу А, совершаемую газом при адиабатическом процессе, в результате которого температура газа понижается от Т₁ до T₂. Учтем формулы (15) и (9), получим

Адиабатический процесс широко применяется на практике. На­пример, в дизельных двигателях воспламенение жидкого топли­ва происходит при быстром адиабатическом сжатии воздуха в цилиндре. Кроме того адиабатический процесс — это один из основных процессов, рассматриваемых в теории тепловых дви­гателей.

Источник

Адиабатический процесс — условия протекания, уравнения и формулы

История открытия

Ряд экспериментов, проведенных в начале XIX столетия, доказали существование атмосферного давления. Так, немецкий инженер Герике сконструировал магдебургские полушария. Из сферы выкачивался воздух, после чего они с трудом разъединялись — воздух давил на них.

Пример еще одного исследования, целью какого является изучение такого явления — опыт Роберта Бойля. Физик доказал, что если трубка запаяна с короткого конца, а в длинный налита ртуть, последняя не поднимется до верха. Ведь воздушными потоками уравновешивается давящая сила.

Ламберт издал в 1779 году книгу «Пирометрия». В его труде описывается повышение и понижение температуры в приемнике воздушного насоса, когда движется поршень. Этот эффект подтвердили следующие ученые:

Дальтон опубликовал доклад, где называется особенность сгущения идеального газа. При нем выделяется тепло.

Обобщил накопившиеся знания Пуассон. По его мнению, температура при адиабатической реакции непостоянная, а, значит, закону Бойля — Мариотта необходима поправка — физик обозначил ее, как коэффициент k и выразил через соотношение теплоемкостей.

Важные нюансы

Термодинамический процесс в общем случае включает в себя теплообмен, работу, совершаемую системой и изменение внутренней энергии. Адиабатный по причине отсутствия обмена теплом сводится к последним двум.

Поэтому для него первое уравнение термодинамики приобретает вид: Δ U = — A. Приняты указанные обозначения:

1. Δ U — преобразование внутренней мощности.
2. A — прилагаемые внешней средой усилия.

Энтропия (S) не меняется в результате теплопередачи. Этот постулат описывается уравнением ΔS = ΔT=0. Здесь T — температура.

А также для расчетов используется такая величина, как адиабата идеального газа. Она обозначается буквой γ и вычисляется следующим образом: γ = C1/C2 (соотношение теплоемкостей).

Может подобный параметр выражаться и как количество степеней свободы. То есть γ = i + 2/ i.

Описание основных циклов

Физиками предлагается указанное определение процесса Карно: это идеальная цикличность, обеспечивающая работу тепловой машины с максимальным КПД. Наибольший и наименьший уровень разогрева совпадает с аналогичными показателями для рабочего устройства.

Среди условий для достижения нужного коэффициента полезного действия физики называют обратимость реакции, значит, следует исключить теплообмен между телами. Соответственно, преобразование тепла происходит лишь изотермически.

Обратный переход рабочего двигателя в исходную точку невозможен. Дело в том, что вся энергия затратится на восстановление изначального положения.

Работа четырехтактной двигательной системы осуществляется по схеме Отто, включающую в себя впуск, сжатие, рабочий вход и выпуск. Второй, третий и четвертый этапы считаются адиабатическими.

Прилагаемые в конце усилия равны разности мощности, с которой давят на газ и силы, затраченной на сжимание. Последнее повторяется до 7 раз (применяемая смесь зажигается принудительно).

Особенность адиабатической реакции заключается в невозможности теплообмена между окружающим пространством и объектом. С ее помощью можно объяснить, каким принципам подчиняется работа двигателя с четырьмя тактами и устройство с высокой отдачей.

Источник

Адиабатический процесс

Адиабатический процесс. Если сосуд с расширяющимся газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. Q = 0. Процесс, происходящий при соблюдении этого условия, называется адиабатическим.

Уравнение первого начала термодинамики при учете условия Q = 0 прини­мает вид

0 = ΔU + A или A = – ΔU. (109)

Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательна (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают.

Адиабатический процесс можно реализовать практически и при отсутствии хорошей теплоизоляции. Но тогда необходимо вести процесс столь быстро, чтобы за время его осуществления не произошел сколько-нибудь существенный теплообмен с внешней средой.

Теплоемкость при адиабатическом процессе

. (110)

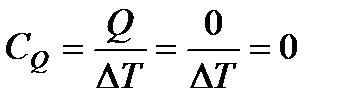
Выведем уравнение кривой, изображающей адиабатический процесс на рV-диаграмме. Уравнение состояния моля газа имеет вид:

При бесконечно малом изменении состояния совершаемая работа А = pdV, а изменение внутренней энергии, согласно (83), ΔU –> C_VdT. Подставляя эти значения A и ΔU в уравнение первого начала термодинамики (109), получим:

Это есть уравнение адиабаты в дифференциальной форме. Поскольку оно содержит все три параметра — р, V и Т, — то для исключения одного из них воспользуемся уравнением состояния (111), предварительно продифференцировав его:

pdV + Vdp = RdT. (113)

Умножая уравнение (112) на R, а (113) — на С_V искладывая их, получим

Принимая во внимание, что для идеального газа C_V + R = = С_р, разделим уравнение (114) на произведение C_VpV и введем обозначение

. (115)

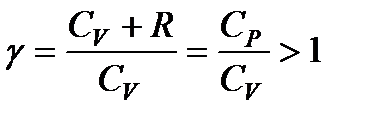
Тогда (114) примет вид

. (116)

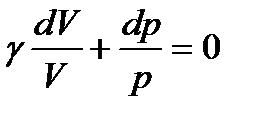
Учитывая, что постоянный множитель γ можно внести под знак дифференциала, преобразуем (116) к виду

Отсюда следует, что величина, стоящая в скобках, должна быть постоянной. Обозначим эту константу как ln(const). Тогда

γlnV + lnp = ln(const). (118)

Учитывая, что γlnV = lnV γ и потенцируя выражение (118), получим

Это и есть уравнение адиабаты. Его также называют уравнением Пуассона.

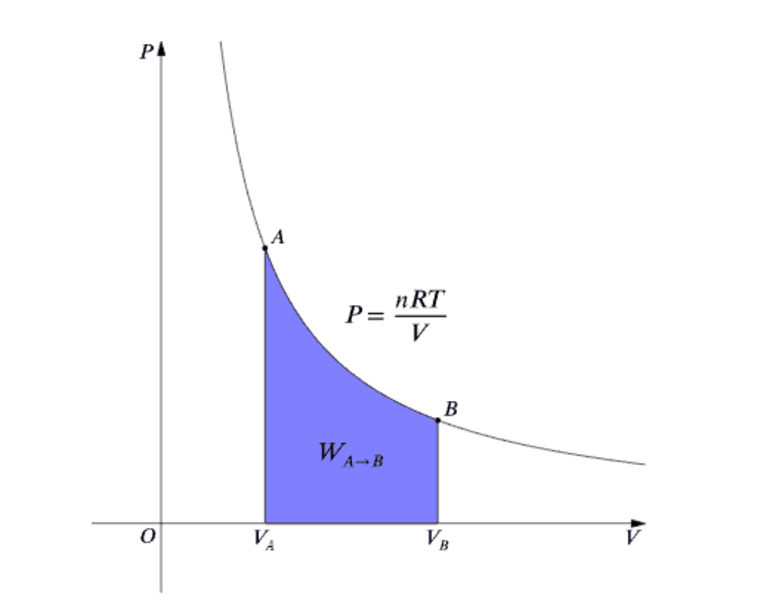
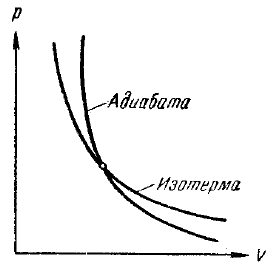
Поскольку γ > 1. то кривая, изображаемая этим уравнением (рис. 39), идет круче изотермы pV = const, которая для сравнения показана на том же чертеже штрих-пунктиром. Видно, что при адиабатическом расширении из точки I кривая (119) опускается ниже изотермы, т. е. газ охлаждается, а при адиабатическом сжатии кривая (119) поднимается выше изотермы, т. е. газ нагревается. Величина работы адиабатического процесса может быть особенно просто вычислена с помощью уравнения (109):

Используя формулу (115), выражение (120) можно преобразовать к виду:

(121)

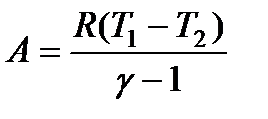
Для нахождения же конечной температуры T₂ можно, комбинируя (111) и (119), получить соотношение

TV γ –1 = const. (122)

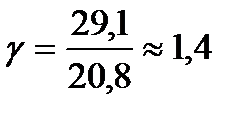
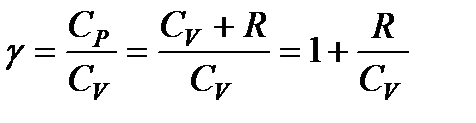
Для одноатомного газа C_v = 12,5 кДж/(кмоль*К), С_P = C_v + R = 20,8 кДж/(кмоль*К), и показатель степени адиабаты равен примерно 1,67. Для двухатомных газов при обычных температурах . Для многоатомных газов при возбуждении их колебательных степеней свободы теплоемкости С_P и C_v имеют еще большие значения и показатель степени адиабаты

(123)

еще ближе к единице.

В быстроходных двигателях внутреннего сгорания и при истечении газов через сопла реактивных двигателей процесс расширения газа протекает настолько быстро, что его можно считать практически адиабатическим и рассчитывать по уравнению (119).

Рис. 39. Адиабата и изотерма

Так как у> 1, то из (122) следует, что при адиабатическом сжатии газ нагревается, а при адиабатическом расширении — охлаждается. Это явление находит применение в дизелях, где воспламенение горючей смеси осуществляется путем адиабатического сжатия. Нагревание газа при адиабатическом сжатии объясняется тем, что во время сжатия над газом производится работа, которая идет на увеличение его внутренней энергии. А так как внутренний энергия идеального газа зависит только от температуры, то это увеличение внутренней энергии проявляется в повышении его температуры. Аналогично объясняется и охлаждение газа при адиабатическом расширении. Охлаждение газа при адиабатическом расширении используется в холодильных машинах.

Источник

Какой процесс называется адиабатным

Адиабатный или адиабатический процесс — медленно протекающий процесс при отсутствии обмена тепловой энергией с окружающей средой.

Этапы открытия

1. С помощью ряда исследований в XVII веке было открыто существование атмосферного давления. Впервые явление подтвердилось магдебургскими полушариями, сконструированными немецким инженером Герике. Сфера, образованная полушариями, освобождается от воздуха. После этого полушария достаточно сложно разъединялись, так как на них действовало давление внешнего воздуха. В ходе другого эксперимента изогнутая стеклянная трубка запаивалась с короткого конца, а длинное колено постоянно наполнялось ртутью. Металл не мог достичь верхнего уровня, так как сжатый воздух уравновешивает давление. Данное исследование в начале провел Роберт Бойль. По итогам проделанных испытаний в 1662 году было сформулировано уравнение закона Бойля — Мариотта.
2. В 1779 году в «Пирометрии» Ламберт описал исследование, в ходе которого повышалась и понижалась температура в приемнике воздушной помпы во время движения поршня. В дальнейшем эффект был подтвержден опытами Дарвина в 1788 году и исследованиями Пикте в 1798 году.
3. Позднее в 1802 году была опубликована работа Дальтона, в которой было рассмотрено выделение тепла при сгущении газов, и их охлаждение при разрежении.
4. Лионский физик Моле сообщил в 1803 году о практическом эксперименте, когда рабочему оружейного завода удалось зажечь трут в дуле духового ружья с помощью сжатия воздуха.
5. Физик Пуассон посвятил свои труды теоретическому обобщению экспериментальных наработок. Адиабатический процесс характеризуется непостоянной температурой, что необходимо обозначить поправкой. Такая корректировка была выведена Пуассоном в виде коэффициента, выраженного с помощью соотношения теплоемкостей. Экспериментальное подтверждение данного коэффициента было зафиксировано в 1807 году Вальтером и Гей-Люссаком, а также в 1819 году получил более точное определение с помощью исследований Дезормома и Клемана.
6. Работа ученого С. Карно «Движущая сила огня», опубликованная в 1824 году, предлагает практическое использование адиабатического процесса.

Уравнение процесса

Адиабатный процесс происходит при одновременном изменении всех трех параметров газообразного вещества V, p, Т. Зависимость данных величин друг от друга представлено формулой Клапейрона-Менделеева. В дополнении для описания процесса применяют уравнение Пуассона, в котором отражена зависимость параметров давления и объема газа. Применяя первый принцип термодинамики к адиабатному процессу идеального газа, можно вывести следующее уравнение:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исключая из формулы выражение \(dT\) по уравнению Клапейрона-Менделеева, получается следующее соотношение:

\(dT=\frac<1>\left(pdV+V dp \right)\)

В итоге получается уравнение:

Согласно уравнению Майера:

Необходимо подставить эту формулу, а также поделить числитель и знаменатель дроби перед скобками на \(CV\) и обозначить \(CP/CV\) — \(\gamma\)

Из чего следует:

\(V dp + \gamma pdV=0\)

Почленно поделив уравнение на произведение \(pV\) , можно вывести следующую формулу:

Если данную формулу проинтегрировать, то в результате получится следующее соотношение:

\(\ln p+\gamma \ln V=\ln C\)

Где С представляет собой постоянную интегрирования.

Если пропотенциировать последнюю формулу, то в итоге получается уравнение Пуссона

Следует отметить, что \(\gamma\) определяется природой газообразного вещества. К примеру, для воздуха \(\gamma=1,42.\)

Как провести процесс, что необходимо

Адиабатный процесс представляет собой термодинамический процесс, для которого необходима теплоизолированная система и полное отсутствие теплообмена с окружающей средой. Во время практического опыта \(Q\;=\;0\) . Исходя из первого закона термодинамики, вся выполненная работа расходуется, чтобы изменить внутреннюю энергию системы:

В условиях реальности подобных результатов достичь практически невозможно. Это связано с отсутствием идеальных изоляторов тепла. Однако существуют способы приблизиться к подобным условиям. К примеру, с помощью применения оболочек с низкими показателями теплопроводности, функционирующих по принципу термоса. Также при достаточно высокой скорости осуществления адиабатного процесса обмен теплом между системой и окружающей средой будет длиться в течение непродолжительного времени, поэтому им можно пренебречь.

Как определить работу газа в адиабатном процессе

Во время опыта можно определить следующие характеристики:

Согласно первому принципу термодинамики, адиабатный процесс в таком случае будет записан следующим образом:

\(\delta Q+\delta A=0\)

Из данного уравнения можно сделать вывод, что:

Таким образом, особенностью адиабатного процесса является выполнение работы исключительно за счет внутренней энергии системы.

В условиях идеального газа формула приобретает следующий вид:

Таким образом, наблюдается снижение температуры газа по причине его работы, направленной против внешних сил, в условиях адиабатного процесса. При этом, если работа выполняется над газообразным веществом, его температура будет повышаться.

Применение адиабатного процесса в машинах

К процессам адиабатного сжатия и расширения газообразных веществ относят также сгущение и разрежение звуковых волн, которые наблюдаются в газах. Скорость звука достаточно велика и в воздухе составляет 340 метров в секунду. Поэтому при таких адиабатических процессах корректно пренебречь теплообменом, ввиду слишком короткого промежутка времени его протекания.

Подобный принцип применим в некоторых тепловых агрегатах. Кроме того, наблюдать адиабатическое сжатие воздуха и, как следствие, повышение его температуры можно при накачивании велосипедной камеры с помощью ручного насоса.

Путем быстрого сжатия газообразного вещества получают в результате возрастание внутренней энергии, которая соответствует величине выполненной работы. В итоге такого процесса температура газа повышается. Данное явление послужило основой инженерного решения, при котором топливная смесь самовозгорается в дизельных моторах.

В обратной ситуации, когда газ сам выполняет определенную работу, стремительно расширяясь, показатели внутренней энергии падают, температурные характеристики газообразного вещества также снижаются. Данное свойство используют для сжижения газов. Адиабатный процесс проявляется так же, как взрыв, плавление предохранителя при коротком замыкании.

Источник