Способы развертки способ раскатки

Способы развертки способ раскатки

При построении разверток данным способом поверхность цилиндра или призмы разрезается по одной из образующих или по одному ребру и совмещается вращением вокруг образующей или вокруг ребра с некоторой плоскостью.

Данный способ обычно применяется в случае, когда образующие цилиндра или ребра призмы являются линиями уровня. Если образующие цилиндра или ребра призмы не являются линиями уровня, то предварительно одним из способов преобразования комплексного чертежа их надо привести в положение линий уровня.

Рассмотрим построение чертежа развертки поверхности призмы, ребра которой являются фронтальными линиями уровня, а нижнее основание является горизонтальной плоскостью уровня (рис. 153).

Призма разрезана по ребру a(a₁,a₂) и это ребро принято за ось вращения i(i₁,i₂); i=α. При вращении граней призмы вокруг этой оси любая точка будет перемещаться в плоскости, перпендикулярной оси вращения, например, точка B будет перемещаться в плоскости

Грань ABB’A поворачивают до совмещения ее с плоскостью уровня α(α₁), проходящей через ребро a. Для этого достаточно совместить точку B с плоскостью α. Зная расстояние от точки A до точки B (/AB/=/A₁B₁/ ) и зная, что точка B перемещается во фронтально-проецирующей плоскости δ(δ₂), из точки A₂, как из центра, проводится дуга окружности радиусом r=/A₁B₁/ и на δ₂ получается точка B₀. Точка B₀ – совмещенное с плоскостью α положение точки B. Соединив точки A₂ и B₀, получим совмещенное положение грани с плоскостью α.

Для того чтобы совместить грань ABB’A’ с плоскостью α, из точки B₀ строится прямая b₀ (b₀ – совмещенное положение ребра b с плоскостью α) параллельно a₂. Аналогичным образом построены совмещенные положения остальных граней призмы с плоскостью  (равенство соответствующих отрезков обозначено на рис 153 специальными значками).

Вершины A’, B’ и C’ верхнего основания также вращаются в соответствующих фронтально-проецирующих плоскостях, перпендикулярных ребрам призмы. Поэтому совмещенные с плоскостью α проекции вершин верхнего основания A’₀, B’₀ и C’ определяются как точки пересечения прямых a₀, b₀ и c₀ с соответствующими фронтально-проецирующими плоскостями.

Соединив последовательно совмещенные вершины ломаными линиями, получают развертку боковой поверхности призмы.

Чтобы получить полную развертку поверхности призмы, к развертке боковой поверхности присоединяют натуральные величины обоих оснований.

На рис 146 показано построение на чертеже развертки точки K(K₁,K₂), принадлежащей грани ABB’A’.

Для этого через точку K проведена прямая (KD) , параллельная ребрам призмы. Затем она построена на чертеже развертки: где K₀ – точка развертки, соответствующая точке K поверхности.

Рассмотрим построение чертежа развертки поверхности наклонного цилиндра, образующие которого являются фронтальными линиями уровня, а основание – окружностью (рис. 154).

Для построения развертки цилиндр разрезается по образующей AA’, а основание цилиндра разбивается на произвольное число равных частей, что соответствует замене цилиндрической поверхности поверхностью многогранной призмы. Следует иметь в виду, что чем больше число сегментов, тем точнее развертка поверхности.

В данном примере основание разбито на шесть равных частей точками A, B, C, D, E и F. Эти точки совмещены с плоскостью γ(γ₁) вращением вокруг оси i(i₁,i₂), которая совпадает с образующей цилиндра AA’.

При вращении граней вписанной призмы вокруг оси i, любая точка будет перемещаться в плоскости, перпендикулярной оси вращения, например, точка B будет вращаться в плоскости δ(δ₂) ⊥ i(δ₂ ⊥ i₂). Зная расстояние от точки A до точки B (AB=A₁B₁) и зная, что точка B перемещается во фронтально – проецирующей плоскости δ(δ₂), можно провести дугу окружности из точки A₂, как из центра, радиусом r = A₁B₁ и получить на δ₂ точку B₀. Точка B₀ – совмещенное с плоскостью γ положение точки B.

Аналогичным образом построены совмещенные положения остальных точек основания цилиндра. Образующие цилиндра на развертке параллельны своим фронтальным проекциям.

Оставшуюся неподвижной точку A и полученные точки, B₀, C₀, D₀, E₀, F₀ и A₀ нужно соединить плавной кривой. Эта кривая представляет собой развертку окружности, лежащей в основании цилиндра.

Источник

Способ раскатки

Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ раскатки используют для построения развертки призмы, в том случае, когда ее основание параллельно какой-либо одной плоскости проекции, а боковые ребра отображаются в натуральную величину на другой плоскости проекций.

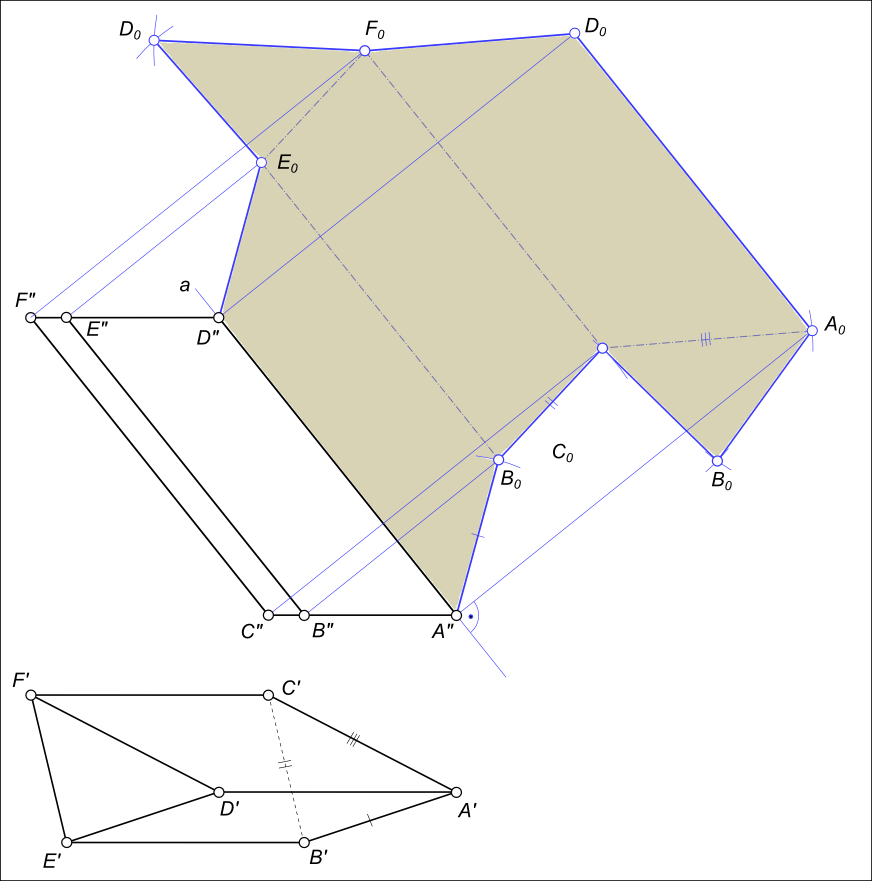
Построить развертку поверхности наклонной трехгранной призмы ABCDEF, используя способ раскатки

За плоскость развертки примем плоскость β, проходящую через ребро AD, параллельную фронтальной плоскости проекций. Совместим грань ADEB с плоскостью β. Для этого мысленно разрежем призму по ребру AD, и затем выполним поворот грани ADEB вокруг ребра AD. Определение совмещенного с плоскостью β положения ребра B₀E₀ из точки B» опускаем луч, перпендикулярный к A»D» и засекаем на нем дугой радиуса A`B`, проведенной из центра A», точку B₀. Из точки B₀ проводим прямую B₀E₀, параллельную A»D». Совмещенное положение ребра B₀E₀ принимаем за новую ось и вращаем вокруг нее грань BEFC до совмещения с плоскостью β. Из точки C» опускаем луч, перпендикулярный к B»E», а из точки B₀ — дугой окружности радиусом B`C` засекаем на нем положение точки C₀. Из C₀ проводим C₀F₀ параллельно B₀E₀. Аналогично определяется положение ребра A₀D₀. Соединив точки A»B₀C₀A₀ и D»E₀F₀D₀ прямыми, получим фигуру A»B₀C₀A₀D₀E₀F₀D» — развертку боковой поверхности призмы. Полная развертка призмы будет получена если к каким-либо из звеньев ломаных линий A»B₀C₀A₀ и D»E₀F₀D₀ пристроить треугольники основания A₀B₀C₀ и D₀E₀F₀.

Способ раскатки применяется также для получения развертки цилиндрической поверхности: Развертка цилиндра

Источник

Способ раскатки

Способ раскатки применяется для построения разверток призматических и цилиндрических поверхностей в случае, когда боковые ребра призмы или образующие цилиндра параллельны какой-либо плоскости проекций, следовательно, проецируются в натуральную величину, а стороны основания параллельны другой плоскости проекций.

Схема построения развертки:

1. Мысленно разрезается боковая поверхность по одному из ребер.

2. Последовательным вращением вокруг боковых ребер, как вокруг линий уровня, все боковые грани совмещаются с плоскостью уровня, проходящей через ребро, по которому разрезается данная призма.

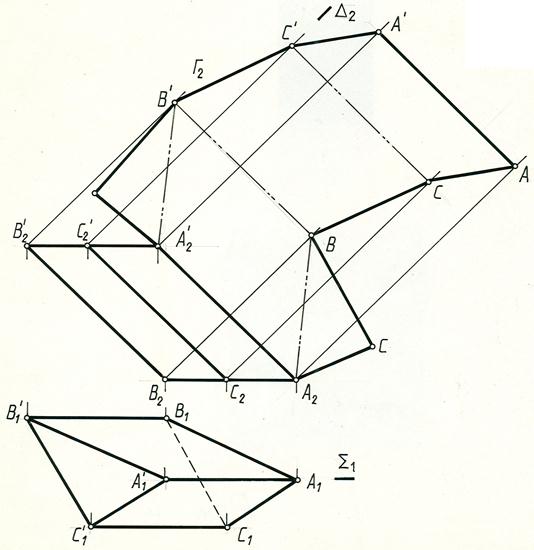
Пример 5. Построить полную развертку поверхности наклонной треугольной призмы.

Решение: Развертку боковой поверхности призмы строим способом раскатки, так как боковые ребра ее параллельны фронтальной плоскости проекций, а стороны основания параллельны горизонтальной плоскости проекций и проецируются в натуральную величину (рис. 12.6)

Так как боковые ребра параллельны фронтальной плоскости П₂, можно каждую грань повернуть вокруг соответствующего ребра до положения, когда эта грань окажется параллельна плоскости П₂. Тогда она и спроецируется на плоскость П₂ без искажения. Повернув таким образом каждую грань, получим развертку боковой поверхности призмы.

Примем за плоскость развертки плоскость Σ (Σ₁), проходящую через ребро АА’, и параллельную фронтальной плоскости проекций. Совместим грань АА’В’В с плоскостью Σ. Для этого мысленно разрежем поверхность призмы по ребру АА’ и повернем грань АА’В’В вокруг ребра (как вокруг фронтали) до совмещения с фронтальной плоскостью Σ, проходящей через это ребро.

Для определения совмещенного положения ребра ВВ’ с плоскостью Σ, из точки В₂‘ проводим вырожденную проекцию плоскости Г(Г₂) , в которой вращается точка В’, (см. метод вращения вокруг линии уровня) перпендикулярную АА’, на которой из точки А’₂ делаем засечку дугой окружности радиуса A₂‘B’=A₁B₁. Через точку В’ проводим прямую В’В параллельную А’А. Принимаем совмещенное положение ребра В’В за новую ось и вращаем вокруг нее грань В’ВСС’ до совмещения с плоскостью Σ. Для этого из точки C₂‘ проводим вырожденную проекцию плоскости Δ (Δ₂) перпендикулярную ребру ВВ’, а из точки В’ – дугу окружности радиусом равным B₁C₁. Пересечение дуги с Δ ₂ определит положение точки С’. Аналогично определяем положение ребра А’А. Соединив соответствующие точки прямыми линиями, получим развертку боковой поверхности призмы. Достроив основание призмы, получим полную развертку.

Источник

Способ раскатки

Способ раскатки рекомендуется для построения развертки цилиндрической поверхности, когда ее образующие являются прямыми уровня, то есть параллельными одной из плоскостей проекций.

Рассмотрим данный способ на примере эллиптического цилиндра с круговым основанием, которое проецируется на горизонтальную плоскость проекций без искажения (в натуральную величину).

Построение развертки данного цилиндра выполняем в следующей последовательности (рис. 168):

1. Делим окружность основания цилиндра на 12 равных частей.

2. Вписываем в цилиндр призму, боковые ребра которой совпадают с образующими цилиндра, проходящими через точки деления основания (рис. ).

3. Принимаем за плоскость развертки фронтальную плоскость (_H), которая проходит через ребро призмы, совпадающее с очерковой образующей цилиндра (1).

4. Находим натуральную величину первой грани, проходящей через ребро 1, для чего вращаем ее вокруг фронтали 1”до уровня этой фронтали. При этом точка 2”переместится по направлению, перпендикулярному к этой фронтали в положение 2, которое найдем, если из точки 1”это направление засечем отрезком 1’2′.

Из точки 3”проводим также перпендикуляр к ребру 1(1”) и находим точку 3, отсекая этот перпендикуляр из точки 2 отрезком 2’3′ и т.д.

Соединяя найденные точки плавной кривой получим фигуру развертки, которую можно представлять себе как отпечаток цилиндра, полученный путем его качения по фронтальной плоскости, проходящей через образующую 1.

Приближенные построения разверток

Развертку неразвертывающихся поверхностей вращения строят приближенно.

1. СПОСОБ ЦИЛИНДРОВ. Способ состоит в том, что данную поверхность вращения разбивают с помощью меридианов на сравнительно узкие, равные между собой доли. Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается данной поверхности в точках среднего меридиана доли. Этот средний меридиан будет вместе с тем нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.

Пример. Построить развертку данной сферы (рис. 169). Разобьем сферу при помощи меридианов на шесть равных частей. Рассмотрим построение приближенной развертки одной части сферы, средним меридианом которой является главный меридиан f.

Прежде всего заменим эту часть сферы цилиндрической поверхностью, описанной около нее. Образующие этой поверхности будут фронтально проецирующими прямыми и поэтому проецируются в натуральную величину на горизонтальную плоскость проекций H. Нормальным сечением цилиндрической поверхности будет половина главного меридиана f, а границами поверхности будут плоскости меридианов, ограничивающих рассматриваемую часть.

Для построения развертки этой цилиндрической поверхности заменяем ее вписанной призматической поверхностью. Для этого делим половину главного меридиана на шесть равных частей и через точки деления проводим образующие цилиндрической поверхности. Затем спрямляем полумеридиан f в отрезок прямой и через его точки деления проводим перпендикулярно к нему образующие EF = EF = E₁F₁,CD=CD=C₁D₁и т.д.

Соединив концы этих образующих плавными кривыми, получим приближенную развертку одной доли данной сферы, равной 1/6 ее части. Развертки остальных долей являются повторением первой.

Обычно сферу разбивают на двенадцать и более частей для получения более точной ее развертки.

2. СПОСОБ КОНУСОВ. Этот способ состоим в замене неразвертывающихся поверхностей такой другой поверхностью, которая составлена из нескольких конических и, следовательно, развертываемых элементов.

Построение развертки способом конусов показано на примере поверхности вращения произвольного вида (рис. 170).

Разделим данную поверхность на несколько поясов, проходящих через точки 1(1”), 2(2”), 3(3”) главного меридиана (рис. ).

Каждый из трех выделенных поясов заменим конусом: первый и второй — описанным около данной поверхности, а третий — вписанным в эту поверхность (рис. 170).

Построение приближенной развертки заданной поверхности сводится к построению разверток трех конусов.

Границами между отдельными частями развертки являются параллели развертываемой поверхности вращения, переходящие в дуги окружностей, которые должны совпадать. Так, длины дуг, имеющих радиусы R₂ иR₃ и радиусыR₄ иR₅, попарно равны и могут легко определяться построением, как показано на рис. 109.

Источник