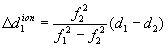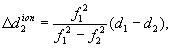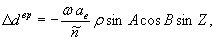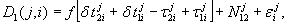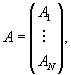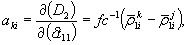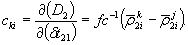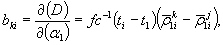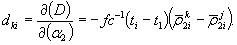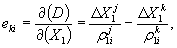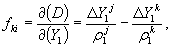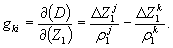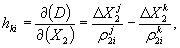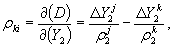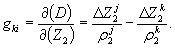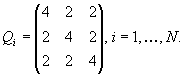Способы разрешения неоднозначности фазовых измерений

1 Область применения

Настоящий стандарт распространяется на методы и технологии выполнения геодезических и землеустроительных работ с использованием аппаратуры потребителей глобальной навигационной спутниковой системы.

Настоящий стандарт устанавливает методы определения целочисленных параметров измеренных фазовых псевдодальностей до космических аппаратов спутниковых систем типа GPS , выполняемую при высокоточных определениях относительных координат пунктов с использованием наблюдений космических аппаратов этих систем, при выполнении геодезических и землеустроительных работ.

2 Обозначения и сокращения

В настоящем стандарте применяют следующие сокращения:

ГЛОНАСС — глобальная навигационная спутниковая система Российской Федерации;

КА — космический аппарат;

МНК — метод наименьших квадратов;

СКП — среднее квадратическое отклонение;

GPS — глобальная навигационная спутниковая система Соединенных Штатов Америки.

3 Общие положения

3.1 Величина фазовой псевдодальности выражается в виде целого числа длин волн и дробной части длины волны. Дробная часть фазы может быть получена с высокой точностью, характеризуемой СКП на уровне первых единиц миллиметров. Прямое измерение целочисленной части фазы не представляется возможным, вследствие чего возникает неоднозначность фазовых измерений, требующая разрешения.

3.2 Разрешение неоднозначности фазовых измерений псевдодальности представляет собой процесс нахождения целого числа циклов (волн), укладывающихся в расстоянии между навигационным спутником и приемником при обработке фазовых измерений.

3.3 Для решения этой задачи с точностью, требуемой для выполнения геодезических и землеустроительных работ, применяют специальные методы математической обработки фазовых измерений, использующие при обработке не сами измерения, а их разности: первые, вторые и третьи. Это позволяет существенно уменьшить число определяемых параметров без ущерба для точности координатных определений. Основными методами разрешения неоднозначности фазовых измерений псевдодальности являются методы, базирующиеся на использовании вторых разностей фаз. Вторые разности вычисляются с использованием первых разностей фаз.

3.4 Решения, получаемые по вторым разностям фаз, как правило, позволяют при нормальных условиях наблюдений вычислить значения целочисленных параметров комбинаций измеренных фаз и на этой основе определять относительные координаты определяемых пунктов с точностью порядка первых единиц миллиметров.

3.5 Исходными данными, необходимыми для разрешения неоднозначности фазовых измерений, являются:

— фазовые измерения на двух несущих частотах для всех наблюдаемых навигационных спутников ГЛОНАСС и GPS на интервале непрерывного слежения за фазой;

— абсолютные геоцентрические координаты исходного пункта;

— предварительные координаты определяемого пункта.

4 Алгоритм разрешения неоднозначности

4.1 Предварительная обработка фазовых измерений

В измеренные значения фаз несущих вводятся поправки за влияние тропосферы, ионосферы и вращения Земли вокруг своей оси.

Поправки за влияние тропосферы вычисляются одним из существующих методов (например, методы Саастомойнена и Хопфилда). При длине измеряемого базиса не более 5 км введение поправок за тропосферу может быть пропущено.

Поправки за влияние ионосферы могут вычисляться с использованием двухчастотных синхронных измерений кодовых и фазовых псевдодальностей. Поправки за влияние ионосферы для фазовых ПД численно равны поправкам, полученным для кодовых ПД, но знаки их противоположны (поправки к кодовым ПД отрицательны, а поправки к фазовым ПД положительны). В случае измерений кодовых ПД формулы для вычисления этих поправок соответственно на первой и второй частотах имеют вид:

где f ₁ f ₂ — значения первой и второй несущих частот;

d ₁ , d ₂ — значения измеренных кодовых ПД соответственно на первой и второй частотах. Поправка на вращение Земли вокруг своей оси за время распространения сигнала от КА до пункта наблюдения (в метрах) вычисляется по формуле:

где ω — угловая скорость вращения Земли вокруг своей оси;

а_е — большая полуось общеземного эллипсоида;

ρ — расстояние до КА (в метрах);

с — скорость света, равная 299792498 м/с;

В — широта пункта наблюдения;

A , Z — соответственно азимут и зенитное расстояние КА.

4.2 Определение первых разностей фаз

Исходным соотношением служит формула:

где j — номер спутника;

i — номер момента времени измерения t_i ;

1, 2 — номера исходного и определяемого пунктов;

С использованием ряда допущений, практически не влияющих на точность решения, величину S ( j , i ) представляют в виде

где f — несущая частота;

δ t_ni и τ j _ni — поправка к шкале времени и интервал времени прохождения сигналов j -го спутника до n -го пункта в момент t_i ( n = 1, 2);

N j ₁₂ — целочисленный параметр ПРФ при i = 1;

ε j _i — случайная погрешность измерения первой разности фаз.

Формула (5) нелинейна относительно поправки δ t_i в том смысле, что параметр τ j _{( i )} должен быть получен на истинный момент приема сигнала ( t_i + δ t_i ).

Для существенного сокращения числа искомых параметров и повышения точности относительных определений поправки к временным шкалам пунктов представляют в виде:

где δ _İ t_i — поправка к временной шкале М-г o пункта в момент первого измерения;

α _İ — коэффициент линейного ухода временной шкалы М-го пункта;

М — номер пункта (М = 1,2);

Δt_i — промежуток времени между текущим и начальным моментом измерений.

4.3 Определение вторых разностей фаз

Исходным соотношением служит формула

где D ₂ ( j , k , i ) — вторая разность фаз на момент t_i .

С учетом полученных первых разностей фаз вторые разности фаз определяют по формуле

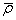
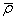
D ₂ (j, k, I) = f ( δ t k _2i — δ t k _2i ) – fc -1 [ρ k _2i + k _{2 i} (δt k _2i – ρ k _2i c -1 )] + fc -1 [ρ k _{1 i} + k _1i
(δt k _1i – ρ k _1i c -1 )] – f (δt j _2i — δt j _1i) + fc -1 [ρ j _2i + 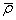j _{2 i} (δt j _2i -ρ j _2i c -1 )] +
+ fc -1 [ρ j _1i + 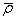j _{1 i} ((δt j _1i — ρ j _1i c -1 )] + N kj ₁₂ + ε kj _i

где N kj ₁₂ — целочисленный параметр ВРФ;

ρ j _{n i} и ρ k _{n i} — мгновенные дальности j -го и k -го спутников от n -го пункта в момент t_i ;

и — скорость изменения дальности j -го и k -го спутников от n -го пункта в момент t_i ;

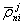
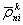
f — частота несущей;

с — скорость света;

ε _i jk — случайная погрешность вторых разностей фаз в момент t _i .

Линеаризация позволяет получить уравнение погрешностей ВРФ, в котором неизвестными являются следующие параметры:

— поправки к предварительным координатам двух пунктов (шесть параметров);

— временные параметры двух пунктов (четыре неизвестных);

— целочисленные параметры, число которых на единицу меньше числа наблюденных спутников.

Систему уравнений погрешностей ВРФ на моменты t ₁ , . , t_N Дописывают матрицей коэффициентов и вектором свободных членов.

Матрица коэффициентов представляют в виде

где N — число моментов измерений ВРФ;

A ₁ , . , A_N — блоки идентичной структуры, зависящие от момента измерений и числа наблюдаемых спутников.

Например, для четырех спутников каждый из блоков A ₁ , . , A_N определяется по формуле

где a_kj и c_ki — коэффициенты при поправках к начальным моментам измерений первого и второго пунктов;

b_kj и d_kj — коэффициенты при скоростях ухода шкал времени первого и второго пунктов;

e_ki , f_ki , g_ki и h_ki , ρ _ki , q_ki — коэффициенты при поправках к предварительным координатам первого и второго пунктов.

Коэффициенты a_kj и c_ki вычисляются по формулам

Коэффициенты b_kj и d_kj вычисляются по формулам:

Коэффициенты e_ki , f_ki , g_ki вычисляются по формулам:

Коэффициенты h_ki , ρ _ki , q_ki вычисляются по формулам:

Коэффициенты при целочисленных параметрах ВРФ образуют единичную матрицу.

Вектор свободных членов системы уравнений погрешностей ВРФ определяется как вектор, элементы которого представляют собой разности ВРФ, вычисляемых по предварительным значениям определяемых параметров, и измеренных значений ВРФ на моменты t ₁ , . , t_N .

Полученную систему уравнений поправок решают по МНК с учетом корреляции ВРФ.

4.4 Учет корреляции вторых разностей фаз

Корреляцию ВРФ учитывают путем использования в решении ковариационной матрицы ВРФ Q . Данная матрица имеет блочно-диагональную структуру. Диагональные блоки являются квадратными матрицами. Их число равно числу N моментов измерений. Размер блока выражается числом, на единицу меньшим числа М наблюдаемых спутников. Например, при М = 4 каждый из указанных блоков имеет вид

4.5 Получение целочисленных параметров вторых разностей фаз

Определяемые параметры ВРФ получают из решения системы нормальных уравнений. Матрицу системы нормальных уравнений формируют в соответствии с формулой

где А Т — матрица, транспонированная по отношению к матрице А;

Р — весовая матрица, обратная по отношению к ковариационной матрице Q .

Вектор свободных членов системы нормальных уравнений формируют по формуле:

где L — вектор свободных членов уравнений погрешностей ВРФ. Из решения системы нормальных уравнений получают:

— поправки к координатам исходного и определяемого пунктов;

— целочисленные параметры ВРФ.

Вследствие погрешностей измерений, плохих условий наблюдений навигационных спутников (многолучевость, искусственные и естественные препятствия наблюдений и т.д.) фактические значения целочисленных параметров, как правило, не являются целыми числами. Поэтому полученные значения этих параметров должны быть округлены до целого в ближайшую сторону. С этими новыми значениями необходимо перевычислить вектор свободных членов уравнений погрешностей и получить новое решение с учетом поправок к шкалам времени пунктов и скоростям их изменения, а также поправок к координатам пунктов.

Ключевые слова: глобальные навигационные спутниковые системы, геодезические и землеустроительные работы, неоднозначность, фазовая псевдодальность

Источник

2.8. Принципы разрешения неоднозначностей при фазовых измерениях

Как уже отмечалось ранее, при определении расстояний до спутников фазовыми методами возникает достаточно сложная проблема разрешения неоднозначности, т. е. нахождения целого числа длин волн N, укладывающихся в измеряемом расстоянии от спутника до приемника. Эта сложность обусловлена, прежде всего, тем, что определяемые дальности оцениваются величинами около 20 ООО км, в то

время как длина волны несущих колебаний в системе GPS составляет всего 0,2 м. При таких исходных предпосылках параметр Охарактеризуется числами порядка 10 8 . Следовательно, для того, чтобы не вносить грубых ошибок в результаты измерений, т. е. уверенно определять величину N с точностью до одной целой единицы, необходимо обеспечить надежное нахождение этой величины с относительной погрешностью менее, чем МО’ 8 . При этом приходится учитывать и такие факторы, как непрерывное изменение величины N из-за орбитального движения спутника, а также необходимость нахождения серии таких величин для нескольких одновременно наблюдаемых спутников, поскольку для каждого конкретного спутника величина N имеет свое индивидуальное значение.

При отработке подходов к выбору эффективных методов разрешения неоднозначности наблюдается стремление выполнить следующие основные предпосылки:

1) перед процедурой, связанной с определением параметра N, целесообразно исключить все основные источники систематических ошибок, которые обусловливают смещение результатов измерений и искажают истинное значение N, не позволяя рассматривать ее как целочисленную величину;

2) для исключения необходимости многократного определения величины TVдля каждого спутника по мере его орбитального движения целесообразно ограничиться нахождением этой величины только в начальной точке наблюдения конкретного спутника, а затем отслеживать ее изменения по показаниям фазоизмерительного устройства;

3) выбираемые методы должны обеспечивать точность предварительных определений значений измеряемых расстояний, связанных с процедурой разрешения неоднозначности, не хуже половинного значения длины волны несущих колебаний, т. е. применительно к GPS на уровне около 10 см;

4) желательно, чтобы предлагаемые методы были достаточно универсальными с тем, чтобы можно было их использовать при работе как с двухчастотными, так и с одночастотными приемниками, в которых исключается возможность использования двух несущих частот с целью разрешения неоднозначности.

При выполнении перечисленных выше предпосылок открывается возможность ограничиться нахождением величины Столько в начальной точке отслеживаемой траектории наблюдаемого спутника, т. е. осуществить разрешение так называемой начальной неоднозначности. Применительно к такой постановке задачи рассмотрим несколько наиболее распространенных методов разрешения неоднозначностей, характерных для спутниковых GPS измерений. К ним относятся:

— метод, базирующийся на комбинации кодовых и фазовых изме-

— метод поиска наиболее вероятных значений величины N;

— нетривиальные методы разрешения неоднозначности.

2.8.1. Геометрический метод

Сущность данного метода состоит в том, что после захвата радиосигнала и начала фазовых измерений непрерывно отслеживаются целочисленные изменения фазы, т. е. циклы. Неизвестная начальная величина N считается при этом неизменной при выполнении измерений во всех последующих точках траектории движения наблюдаемого спутника. Измерения моделируются на основе использования уравнения (2.13):

АФ = — f £ + N + AN + f(St np — + , (2.32)

где А N — отсчитываемые с помощью фазометра целочисленные изменения фазовых циклов, обусловленные движением спутника по орбите. Пояснения обозначений остальных входящих в данную формулу величин было дано ранее.

Интересующее нас значение N включается в число неизвестных. Оно определяется в процессе решения системы уравнений, относящихся к отсчетам при нахождении спутника в различных точках траектории. При этом используются первые и вторые разности дифференциальных измерений, а также доплеровские решения.

Надежность нахождения величины N зависит от длительности наблюдения спутника (чем больше эта длительность, тем надежнее определяется величина N). При этом не допускается пропуск отсчитываемых фазовых циклов, который может возникать в случае временных пропаданий радиосигналов от наблюдаемого спутника (например, изза экранировки этих сигналов окружающими объектами).

К положительным сторонам данного метода следует отнести простоту и четкость постановки задачи при моделировании такой процедуры, возможность его применения при работе на одной несущей частоте, а также сравнительно быстрое достижение поставленной цели.

Негативными сторонами рассматриваемой процедуры разрешения неоднозначности являются такие факторы, как рекомендации, связанные с увеличением длительности сеанса наблюдений, влияние недостаточно полно исключенных систематических погрешностей, обусловленных атмосферой (в частности, ионосферой), положением спутника на орбите и другими факторами, а также необходимость предварительного выявления и последующего устранения пропуска фазовых циклов.

2.8.2. Метод комбинированного использования кодовых

и фазовых измерений

Реализация данного метода базируется, как правило, на совместном применении двухчастотных фазовых и кодовых измерений. С учетом этого рассмотрим основные особенности двухчастотных фазовых измерений применительно к решению проблемы неоднозначности.

При выполнении фазовых измерений на двух передаваемых со спутника несущих частотах L1 и L2 представляется возможным образовать различные комбинации этих измерений и, в частности, их разность:

где ДФ £1 и ДФ 12 — измеряемые GPS-приемником фазовые сдвиги, относящиеся к несущим колебаниям с частотами L1 и L2.

Получаемая при этом разность АФ ДЬ эквивалентна фазовому сдвигу, характерному для разностной частоты AL, номинальное значе-

ние которой равно:

/ a l L = / l i — / l 2

Длина волны таких разностных колебаний равна 86,2 см. Это значение существенно превышает длины волн основных несущих колебаний, которые соответственно равны 19,0 и 24,4 см.

Отмеченный метод перехода к более низкочастотным колебаниям получил название метода широкой дорожки, при использовании которого существенно облегчается нахождение целочисленных значений N на ранней стадии их вычислений.

Для решения поставленной задачи установим взаимосвязь между значениями N, характерными как для основных несущих частот L1 и L2 , так и для их разностей.

В соответствии с формулой (2.13) имеем:

+ N Ll + f Ll (& пр — + Л А,™,,

Дф.2 = — /i2 — +tfi2 +/«( -st c )+f L1 a amML2

В этих формулах атмосферные задержки обусловлены, главным образом, влиянием ионосферы. Модельное представление такого влияния описывается следующим приближенным соотношением:

2 ‘ (2.35) где к — коэффициент, зависящий от концентрации электронов в ионосфере, от длины пути прохождения радиосигнала через ионизированную среду и от скорости электромагнитных волн в вакууме;/— частота несущих колебаний.

Знак «минус» в формуле (2.35) свидетельствует о том, что отдельные спектральные составляющие излучаемых колебаний при прохождении через ионосферу с фазовой скоростью испытывают не торможение, а, наоборот, ускорение.

С учетом приведенных выше предпосылок формулы (2.34) приобретают вид:

причем для разности величин ДФ £1 и ЛФ 12 можно записать:

Источник