Способы разрешения коллизий при хешировании

АЛГОРИТМЫ И СТРУКТУРЫ ДАННЫХ

Электронный учебный материал для студентов всех специальностей факультета Прикладная информатика Кубанского государственного аграрного университета

Поиск

Введите ваш запрос для начала поиска.

Об авторах

Курс разработан на кафедре Компьютерных технологий и систем Кубанского государственного аграрного унивеситета. Авторами являются заведующий кафедрой, доктор технических наук, профессор Лойко Валерий Иванович и доцент кафедры, кандидат физико-математических наук Лаптев Сергей Владимирович.

Основные цели сайта

Сайт предназанчен для максимально эффективного и быстрого доступа ко всем материалам курса «Алгоритмы и структуры данных», имеющимся на кафедре компьютерных технологий и систем КубГАУ. Основной задачей его создания является повышения эффективности освоения дисциплины студентами и всеми желающими.

Алгоритмы хеширования. Методы разрешения коллизий

Разрешение коллизий при хешировании методом открытой адресации

Самым простым методом разрешения коллизий при хешировании является помещение данной записи в следующую свободную позицию в массиве. Например, запись с ключом 0596397 помещается в ячейку 398, которая пока свободна, поскольку 397 уже занята. Когда эта запись будет вставлена, другая запись, которая хешируется в позицию 397 (с таким ключом, как 8764397) или в позицию 398 (с таким ключом, как 2194398), вставляется в следующую свободную позицию, которая в данном случае равна 400.

Этот метод еще называется методом линейных проб, он является примером некоторого общего метода разрешения коллизий при хешировании , который называется повторным хешированием.

В общем случае функция повторного хеширования rh воспринимает один индекс в массиве и выдает другой индекс.

Если ячейка массива h(key) уже занята некоторой записью с другим ключом, то функция rh применяется к значению h(key) для того, чтобы найти другую ячейку, куда может быть помещена эта запись. Если ячейка rh(h(key)) также занята, то хеширование выполняется еще раз и проверяется ячейка rh(rh(h(key))) и т.д.

Алгоритмы метода открытой адресации

Function h(key) – хеш- функция

Function rh(i) — функция повторного хеширования

Procedure insert(key) – процедура вставки ключа в хеш-таблицу

while ((k(i) key) and (k(i) nullkey )) do

if k(i) = nullkey then

Subroutine heshtable – функция создания хеш-таблицы

while not eof do

Subroutine search – функция поиска в хеш-таблице

Источник

Разрешение коллизий

Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.

Содержание

Разрешение коллизий с помощью цепочек [ править ]

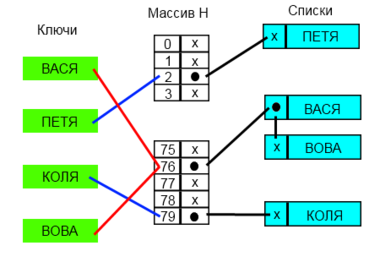
Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math] , либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.

В зависимости от того нужна ли нам уникальность значений операции вставки у нас будет работать за разное время. Если не важна, то мы используем список, время вставки в который будет в худшем случае равна [math]O(1)[/math] . Иначе мы проверяем есть ли в списке данный элемент, а потом в случае его отсутствия мы его добавляем. В таком случае вставка элемента в худшем случае будет выполнена за [math]O(n)[/math]

Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.

Удаления элемента может быть выполнено за [math]O(1)[/math] , как и вставка, при использовании двухсвязного списка.

Линейное разрешение коллизий [ править ]

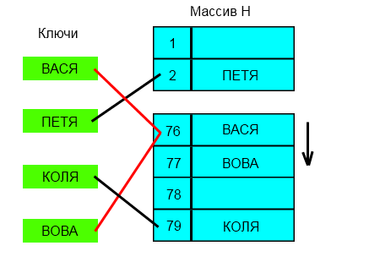
Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.

Стратегии поиска [ править ]

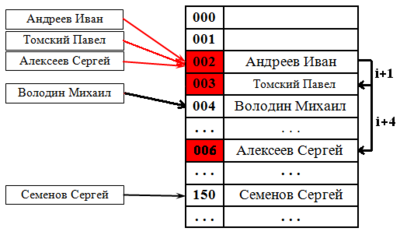
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Выбираем шаг [math]q[/math] . При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск — частный случай линейного, где [math]q=1[/math] .

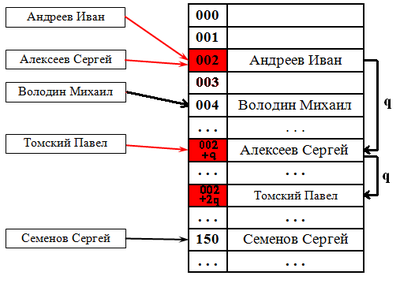
Шаг [math]q[/math] не фиксирован, а изменяется квадратично: [math]q = 1,4,9,16. [/math] . Соответственно при попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math] i+1, i+4, i+9[/math] и так далее, пока не найдём свободную ячейку.

Проверка наличия элемента в таблице [ править ]

Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.

При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.

Проблемы данных стратегий [ править ]

Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.

Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.

Удаление элемента без пометок [ править ]

Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:

• если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
• в цепочке не должно оставаться «дырок», тогда любой элемент с данным хешем будет доступен из начала цепи

Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).

Хеш-таблицу считаем зацикленной

Утверждение (о времени работы):

[math]\triangleright[/math]

Заметим что указатель [math]j[/math] в каждой итерации перемещается вперёд на [math]q[/math] (с учётом рекурсивных вызовов [math]\mathrm[/math] ). То есть этот алгоритм последовательно пройдёт по цепочке от удаляемого элемента до последнего — с учётом вызова [math]\mathrm[/math] собственно для нахождения удаляемого элемента, мы посетим все ячейки цепи.

[math]\triangleleft[/math]

Вариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций

Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.

• В редактируемой цепи не остаётся дырок

Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm[/math] (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.

• Элементы, которые уже на своих местах, не должны быть сдвинуты.

• В других цепочках не появятся дыры

Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.

Двойное хеширование [ править ]

Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.

Принцип двойного хеширования [ править ]

При двойном хешировании используются две независимые хеш-функции [math] h_1(k) [/math] и [math] h_2(k) [/math] . Пусть [math] k [/math] — это наш ключ, [math] m [/math] — размер нашей таблицы, [math]n \bmod m [/math] — остаток от деления [math] n [/math] на [math] m [/math] , тогда сначала исследуется ячейка с адресом [math] h_1(k) [/math] , если она уже занята, то рассматривается [math] (h_1(k) + h_2(k)) \bmod m [/math] , затем [math] (h_1(k) + 2 \cdot h_2(k)) \bmod m [/math] и так далее. В общем случае идёт проверка последовательности ячеек [math] (h_1(k) + i \cdot h_2(k)) \bmod m [/math] где [math] i = (0, 1, \; . \;, m — 1) [/math]

Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за [math]O(1)[/math] , в худшем — за [math]O(m)[/math] , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.

[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]

Выбор хеш-функций [ править ]

[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:

• не равные [math] 0 [/math]
• независимые от [math] h_1 [/math]
• взаимно простые с величиной хеш-таблицы

Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math] . Второй — размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.

Например, если размер таблицы равен [math] m [/math] , то в качестве [math] h_2 [/math] можно использовать функцию вида [math] h_2(k) = k \bmod (m-1) + 1 [/math]

Пример [ править ]

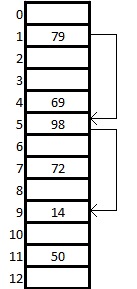
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:

[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]

[math] h_1(k) = k \bmod 13 [/math]

[math] h_2(k) = 1 + k \bmod 11 [/math]

Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math] . Тогда [math] h(14,0) = (h_1(14) + 0\cdot h_2(14)) \bmod 13 = 1 [/math] . Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2\cdot h_2(14)) \bmod 13 = 9 [/math] . Ячейка с номером 9 свободна, значит записываем туда наш ключ.

Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.

Простая реализация [ править ]

Пусть у нас есть некоторый объект [math] item [/math] , в котором определено поле [math] key [/math] , от которого можно вычислить хеш-функции [math] h_1(key)[/math] и [math] h_2(key) [/math]

Так же у нас есть таблица [math] table [/math] величиной [math] m [/math] , состоящая из объектов типа [math] item [/math] .

Реализация с удалением [ править ]

Чтобы наша хеш-таблица поддерживала удаление, требуется добавить массив [math]deleted[/math] типов [math]bool[/math] , равный по величине массиву [math]table[/math] . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.

Альтернативная реализация метода цепочек [ править ]

В Java 8 для разрешения коллизий используется модифицированный метод цепочек. Суть его заключается в том, что когда количество элементов в корзине превышает определенное значение, данная корзина переходит от использования связного списка к использованию сбалансированного дерева. Но данный метод имеет смысл лишь тогда, когда на элементах хеш-таблицы задан линейный порядок. То есть при использовании данный типа [math]\mathbf[/math] или [math]\mathbf[/math] имеет смысл переходить к дереву поиска, а при использовании каких-нибудь ссылок на объекты не имеет, так как они не реализуют нужный интерфейс. Такой подход позволяет улучшить производительность с [math]O(n)[/math] до [math]O(\log(n))[/math] . Данный способ используется в таких коллекциях как HashMap, LinkedHashMap и ConcurrentHashMap.

Источник

Коллизии при хешировании

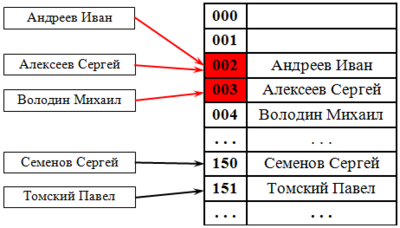
При получении таблицы с помощью преобразования ключей имеет место один недостаток. Предположим, что существуют два различных ключа k1 и k2 (k1  k2) такие, что h(k1) = h(k2). Когда запись с ключом k1 вводится в таблицу, она вставляется в позицию с индексом h(k1). Но когда хешируется ключ k2, получаемая позиция является той же позицией, в которой хранится запись с ключом k1. Ясно, что две записи не могут занимать одну и ту же позицию. Такая ситуация называется коллизией (collision) при хешировании или столкновением. Иногда коллизию называют конфликтом.

В примере с изделиями на рисунке 12.1 коллизия при хешировании произойдет, если в таблицу будет добавлена, например, запись с ключом 0596993. Далее мы будем исследовать возможности, как найти решение в такой ситуации. Следует отметить, что хорошей хеш-функцией является такая функция, которая минимизирует коллизии и распределяет записи равномерно по всей таблице. Поэтому и желательно иметь массив с размером больше, чем число реальных записей. Чем больше диапазон хеш-функции, тем менее вероятно, что два ключа дадут одинаковое значение хеш-функции. Конечно, при этом возникает компромисс между временем и пространством. Наличие пустых мест в массиве неэффективно с точки зрения использования пространства, но при этом уменьшается необходимость разрешения коллизий при хешировании, что, следовательно, является более эффективным в смысле временных затрат.

Алгоритм, который позволяет распределять в таблице записи, конкурирующие с другими записями в одну ячейку хеш-таблицы, называется методом разрешения коллизий (collision resolution).

Разрешение коллизий при хешировании

Посмотрим, что произойдет, если мы попытаемся ввести в таблицу на рисунке 12.1 некоторую новую запись с ключом 0596993. Используя хеш-функцию Кey Mod 1000, мы найдем, что h(0596993) = 993, и что запись для этого ключа должна находиться в позиции 993 в массиве. Однако позиция 993 уже занята, поскольку там находится запись с ключом 0047993. Следовательно, запись с ключом 0596993 должна быть вставлена в таблицу в другом месте.

Разрешение коллизий методом открытой адресации

Самым простым методом разрешения коллизий при хешировании является помещение данной записи в следующую свободную позицию в массиве. Например, на рисунке 12.1 запись с ключом 0596993 помещается в ячейку 994, которая пока свободна, поскольку 993 уже занята. Когда эта запись будет вставлена, другая запись, которая хешируется в позицию 993 (с таким ключом, как 8764993) или в позицию 994 (с таким ключом, как 2194994), вставляется в следующую свободную позицию, индекс которой в данном случае равна 995.

Этот метод называется линейным зондированием или линейным опробованием (linear probing); он является частным случаем некоторого общего метода разрешения коллизий при хешировании, который называется повторным хешированием или схемой с открытой адресацией (open-addressing schemes).

В общем случае функция повторного хеширования rh воспринимает один индекс в массиве и выдает другой индекс. Если ячейка массива с индексом i = h(Кey) уже занята некоторой записью с другим ключом, то функция rh применяется к значению i для того, чтобы найти другую ячейку, куда может быть помещена эта запись. Если ячейка с индексом

j = rh(i) = rh(h(key)) (12.2)

также занята, то хеширование выполняется еще раз и проверяется ячейка rh(rh(h(key))). Этот процесс продолжается до тех пор, пока не будет найдена пустая ячейка.

В нашем примере хеш-функция есть h(key)= Кey Mod 1000, а функция повторного хеширования rh(i)= (i+1) Mod 1000, т. е. повторное хеширование какого-либо индекса есть следующая последовательная позиция в данном массиве, за исключением того случая, что повторное хеширование 999 дает 0.

Поиск в такой таблице выполняется по аналогичному алгоритму:

аргумент поиска ArgSearch хешируется в индекс i = h(ArgSearch);

проверяется i-ая позиция таблицы:

если ArgSearch совпадает с ключом i-ой записи, то поиск результативен (искомая запись имеет индекс i), поиск завершается,

если совпадения не произошло, то переход к п. 3,

или i-ая позиция пуста, поиск безрезультатен, поиск завершен;

выполняется повторное хеширование, т. е. проверяется позиция с индексом

j = rh(i) = rh(h(ArgSearch)),

и результат проверки анализируется так же, как в п. 2.

Рассмотрим данный алгоритм более подробно, чтобы понять, можно ли определить свойства некоторой «хорошей» функции повторного хеширования. Сфокусируем наше внимание на количестве повторных хеширований, поскольку это количество определяет эффективность поиска. Выход из цикла повторных хеширований может быть в одном из двух случаев. Или переменная i принимает такое значение, что ключ с индексом rh(i) равен Кey (и в этом случае найдена запись), или переменная i принимает такое значение, что элемент с индексом rh(i) пуст; в этом случае найдена пустая позиция, и запись может быть вставлена.

Может случиться, однако, что данный цикл будет выполняться бесконечно. Для этого существуют две возможные причины. Во-первых, таблица может быть полной, так что вставить какие-либо новые записи невозможно. Эта ситуация может быть обнаружена при помощи счетчика числа записей в таблице. Когда этот счетчик равен размеру таблицы, не надо проверять дополнительные позиции.

Возможно, однако, что данный алгоритм приведет к бесконечному зацикливанию, даже если имеются некоторые пустые позиции (или даже много таких позиций). Предположим, например, что в качестве функции повторного хеширования используется функция rh(i) = (i+2) Mod 1000. Тогда любой ключ, который хешируется в нечетное целое число, повторно хешируется в следующие за ним нечетные целые числа, а любой ключ, который хешируется в четное число, повторно хешируется в следующие за ним четные целые числа. Рассмотрим ситуацию, при которой все нечетные позиции в таблице заняты, а все четные свободны. Несмотря на тот факт, что половина позиций в массиве свободна, невозможно вставить новую запись, чей ключ хешируется в нечетное число. Конечно, маловероятно, что заняты все нечетные позиции, а ни одна из четных позиций не занята. Но если использовать функцию повторного хеширования

rh(i) = (i+200) Mod 1000,

то каждый ключ может быть помещен только в одну из пяти позиций (поскольку х  Mod 1000 = (х+1000) Mod 1000. При этом вполне возможно, что эти пять позиций будут заняты, а большая часть таблицы будет пустой.

Свойство хорошей функции повторного хеширования состоит в том, что для любого индекса i последовательно выполняемые повторные хеширования rh(i), rh(rh(i)), . располагаются на максимально возможное число целых чисел от 0 до N-1 (где N является числом элементов в таблице), причем в идеале  на все эти числа. Функция повторного хеширования rh(i)= (i+1) Mod N обладает этим свойством. И действительно, любая функция rh(i)= (i+с) Mod N, где c  некоторая константа такая, что значения с и N являются взаимно простыми числами (т. е. они одновременно не могут делиться нацело ни на какое число, кроме 1), выдает последовательные значения, которые распространяются на всю таблицу.

Имеется другая мера пригодности функции хеширования. Рассмотрим функцию повторного хеширования rh(i)= (i+1) Mod N. Предполагаем, что функция хеширования h(Key) выдает индексы, которые равномерно распределены в интервале от 0 до N-1, т.е. вероятность того, что функция h(Key) будет равна какому-либо конкретному числу в этом диапазоне, одинакова для всех чисел. Тогда первоначально, когда весь массив пуст, равновероятно, что некоторая произвольная запись будет помещена в любую заданную пустую позицию в массиве. Однако, когда записи будут вставлены и будет разрешено несколько коллизий при хешировании, это уже не будет справедливо. После большого количества вставок и разрешений коллизий с помощью повторного хеширования может возникнуть следующая ситуация: при вставке записи, у которой ключ хешируется в индекс i, обнаруживается, что i-ая позиция занята записью, ключ которой хешируется в другой индекс.

Явление, при котором два ключа, которые хешируются в разные значения, конкурируют друг с другом при повторных хешированиях, называется скучиванием или скоплекнием. При скучивании в таблице образуются локальные участки, в которых располагаются конкурирующие друг с другом записи, тогда как другие части таблицы оказываются незанятыми. Эти участки называются кластерами.

Одним способом ослабления эффекта скучивания является использование двойного хеширования, которое состоит в использовании двух хеш-функций  h1(key) и h2(key). Функция h1, которая называется первичной хеш—функцией, используется первой при определении той позиции, в которую должна быть помещена запись. Если эта позиция занята, то последовательно используется функция повторного хеширования

до тех пор, пока не будет найдена пустая позиция. Записи с ключами key1 и key2 не будут соревноваться за одну и ту же позицию, если h2(key1) не равно h2(key2). Это справедливо, несмотря на ту возможность, что h1(key1) может в действительности равняться h1(key2). Функция повторного хеширования зависит не только от индекса, который надо повторно хешировать, но также от первоначального ключа. Отметим, что значение h2(key) не нужно еще раз вычислять при каждом повторном хешировании: его необходимо вычислить только один раз для каждого ключа, который надо повторно хешировать. Следовательно, в оптимальном случае функции h1 и h2 должны быть выбраны так, чтобы они выполняли хеширование и повторное хеширование равномерно в интервале от 0 до N1, а также минимизировали скучивание. Такие функции не всегда просто найти.

Кроме линейного опробывания существует несколько других схем с открытой адресацией. Рассмотрим две из них.

При использовании алгоритма квадратичного опробывания (quadratic probing) поиск точки вставки элемента осуществляется путем проверки не следующей по порядку ячейки, а ячеек, которые расположены все дальше от исходной. Если первое хеширование ключа оказывается безрезультатным и ячейка занята, то проверяется следующая ячейка (элемент массива). В случае неудачи проверяется ячейка, которая расположена через четыре ячейки. Если и эта проверка неудачна, то проверяется ячейка расположенная через девять индексов и т. д., причем последующие повторные опробывания выполняются для ячеек, расположенных через 16, 25, 36 и так далее ячеек. Этот алгоритм позволяет предотвратить образование кластеров, однако он может приводить и к ряду нежелательных проблем.

Во-первых, если для многих ключей хеширование генерирует один и тот же индекс, то все их последовательности повторных опробываний будут выполняться вдоль одного и того же пути. В результате образуется кластер, но такой, который кажется распределенным по хеш-таблице. Во-вторых, квадратичное опробывание не гарантирует посещения всех ячеек. Максимум в чем можно быть уверенным, если размер таблицы равен простому числу, это в том, что квадратичное опробывание обеспечит посещение, по меньшей мере, половины всех ячеек хеш-таблицы.

Следующая схема с открытой адресацией  псевдослучайное опробывание (pseudorandom probing). Этот алгоритм требует наличия программного датчика случайных чисел, начальное значение которого можно устанавливать в любой момент. Алгоритм устанавливает следующую последовательность действий. Выполняется первоначальное хеширование ключа, и полученное хеш-значение, передается в датчик псевдослучайных чисел в качестве его начального значения. Генерируется первое вещественное случайное число в диапазоне [0, 1], и оно умножается на размер таблицы (N) для получения целочисленного значения в диапазоне от 0 до N-1. Это значение и будет индексом проверяемого элемента. Если ячейка занята, то генерируется следующее случайное число, умножается на размер таблицы, и ячейка с полученным значением индекса проверяется. Этот процесс выполняется до тех пор, пока не будет найдена пустая ячейка. Поскольку для одного и того же начального значения генератор будет генерировать одни и те же числа в одной и той же последовательности, для одного и того же хеш-значения всегда будет создаваться одна и та же последовательность опробывания.

Источник