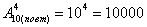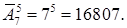Способы размещения с повторениями

1.3.8. Размещения с повторениями

Из множества, состоящего из элементов, выбирается элементов, при этом важен порядок элементов в каждой выборке. И было бы это «обычными» размещениями, но изюминка в том, что любой объект исходного множества мы можем выбирать неоднократно, причём «от множества не убудет»!

Когда так бывает? Ну, конечно, при выборе цифр и букв. Как говорится, если 10 раз сказать «а», то буква «а» из алфавита никуда не денется.

На практике распространена задача с кодовым замком, но по причине развития технологий актуальнее рассмотреть его цифрового потомка:

Задача 14
Сколько существует четырёхзначных пин-кодов?

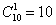
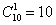
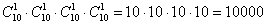
Решение: на самом деле для разруливания задачи достаточно знаний правил комбинаторики: способами можно выбрать первую цифру пин-кода и способами – вторую цифру пин-кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить:
способами.

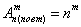
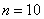
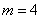
А теперь по формуле размещений с повторениями. По условию, нам предложен набор из цифр, из которого выбираются цифры и располагаются в определенном порядке, при этом цифры в выборке могут повторяться (т.к. любой цифрой можно пользоваться произвольное количество раз). Таким образом:

Ответ: 10000

Что тут приходит на ум… …если банкомат «съедает» карточку после третьей неудачной попытки ввода пин-кода, то шансы подобрать его наугад весьма призрачны.

И кто сказал, что в комбинаторике нет никакого практического смысла?

Ещё одна познавательная и практически важная задача:

Задача 15
Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами).

Сколько различных номерных знаков можно составить для региона?

Не так их, кстати, и много. В крупных регионах такого количества не хватает, и поэтому для них существуют несколько кодов к надписи RUS.

…хотел похвастаться эксклюзивом, да оказалось не эксклюзивом =) Заглянул в Википедию – там есть расчёты, правда, без комментариев.

И теперь во всеоружии мы возвращаемся к основному курсу:

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

12. Размещения с повторениями

Пусть выбор k элементов из некоторого множества, состоящего из n элементов, производится с возвращением и с упорядочением их в последовательную цепочку. Различными исходами такого выбора будут всевозможные наборы (вообще говоря, с повторениями) отличающиеся либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями из n элементов по k элементов.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить девять размещений с повторениями по два элемента: ab, ac, ba, bc, ca, cb, aa, bb, cc.

Таким образом, размещение с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до k включительно или не содержать его совсем, т. е. каждое размещение с повторениями из n элементов по k элементов может состоять не только из различных элементов, но и k каких угодно и как угодно повторяющихся элементов.

Число размещений с повторениями можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Второй элемент также можно выбрать n способами (ведь элементы могут повторяться) и т. д. По принципу умножения находим

. (10.1)

Пример 10.1. В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?

Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:

Пример 10.2. Сколькими способами можно 5 шариков разбросать по 8 лункам, если каждая лунка может вместить все 5 шариков?

Решение. Данная задача есть задача на отыскание числа размещений с повторениями

.

Пример 10.3. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?

Решение. Число всех букв, каждая из которых записывается одним символом, равно .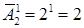

Число всех букв, каждая из которых записывается двумя символами, равно .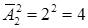

Число всех букв, каждая из которых записывается тремя символами, равно .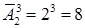

Число всех букв, каждая из которых записывается четырьмя символами, равно .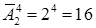

Число всех букв, каждая из которых записывается пятью символами, равно .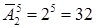

Число всех указанных букв будет равно 62.

10.1. Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?

Ответ: .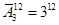

10.2. Сколькими способами Пончик может рассовать 6 конфет по 9 карманам, если каждый карман может вместить все конфеты?

Ответ: .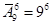

10.3. Сколькими способами можно разместить 8 пассажиров по трем вагонам?

Ответ: .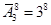

10.4. Сколькими различных восьмизначных чисел можно написать, пользуясь только тремя цифрами 3, 5, 7 при условии, что цифра 5 в каждом числе встречается ровно два раза?

Ответ: .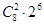

10.5. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа 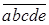(повторение цифр разрешается). Сколько среди них чисел, у которых: 1) a=1; 2) a¹2; 3) a=3, b=2; 4) a=3, b=4, c=5?

Ответ: .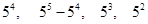

10.6. Сколько чисел, меньших миллиона, можно написать с помощью цифр: а) 8 и 9; б) 7, 8, 9; в) 0, 8, 9 (с цифры 0 число начинаться не может)?

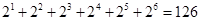
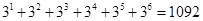
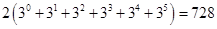
Ответ: а) Так как с помощью двух цифр 8 и 9 можно написать 2k k-значных числа, то общее количество искомых чисел равно . б) Для трёх цифр аналогично получаем . в) Учтём, что для первой цифры есть только две возможности выбора. Тогда получим чисел.

10.7. Имеется три курицы, четыре утки и два гуся. Сколькими способами можно выбрать из них несколько птиц так, чтобы среди выбранных оказались и куры, и утки, и гуси?

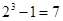
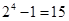
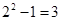
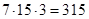
Ответ: Каждая курица может либо войти, либо не войти в число выбранных. Поэтому имеем 23 способов выбора кур. Так как по условию хотя бы одна курица должна быть выбрана (т. е. не может быть случая, когда ни одной курицы не будет выбрано), то число выбора кур будет на единицу меньше: способов выбора кур. Точно так же есть способов выбора уток и способов выбора гусей. Всего способов.

Источник

Перестановки, размещения и сочетания. Формулы.

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме «Понятие множества. Способы задания множеств».

Очень краткий рассказ про множества: показать\скрыть

Если вкратце: множеством именуют некую совокупность объектов. Записывают множества в фигурных скобках. Порядок записи элементов роли не играет; повторения элементов не допускаются. Например, множество цифр числа 11115555999 будет таким: $\<1,5,9 \>$. Множество согласных букв в слове «тигрёнок» таково: $\<т, г, р, н, к\>$. Запись $5\in A$ означает, что элемент 5 принадлежит множеству $A=\<1,5,9 \>$. Количество элементов в конечном множестве называют мощностью этого множества и обозначают $|A|$. Например, для множества $A=\<1,5,9 \>$, содержащего 3 элемента, имеем: $|A|=3$.

Рассмотрим некое непустое конечное множество $U$, мощность которого равна $n$, $|U|=n$ (т.е. в множестве $U$ имеется $n$ элементов). Введём такое понятие, как выборка (некоторые авторы именуют её кортежем). Под выборкой объема $k$ из $n$ элементов (сокращённо $(n,k)$-выборкой) будем понимать набор элементов $(a_1, a_2,\ldots, a_k)$, где $a_i\in U$. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Две упорядоченные выборки, различающиеся лишь порядком элементов, являются различными. Если порядок следования элементов выборки не является существенным, то выборку именуют неупорядоченной.

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Для примера рассмотрим множество $U=\$. Множество $U$ содержит 5 элементов, т.е. $|U|=5$. Выборка без повторений может быть такой: $(a,b,c)$. Данная выборка содержит 3 элемента, т.е. объём этой выборки равен 3. Иными словами, это $(5,3)$-выборка.

Выборка с повторениями может быть такой: $(a,a,a,a,a,c,c,d)$. Она содержит 8 элементов, т.е. объём её равен 8. Иными словами, это $(5,8)$-выборка.

Рассмотрим ещё две $(5,3)$-выборки: $(a,b,b)$ и $(b,a,b)$. Если мы полагаем наши выборки неупорядоченными, то выборка $(a,b,b)$ равна выборке $(b,a,b)$, т.е. $(a,b,b)=(b,a,b)$. Если мы полагаем наши выборки упорядоченными, то $(a,b,b)\neq(b,a,b)$.

Рассмотрим ещё один пример, немного менее абстрактный 🙂 Предположим, в корзине лежат шесть конфет, причём все они различны. Если первой конфете поставить в соответствие цифру 1, второй конфете – цифру 2 и так далее, то с конфетами в корзине можно сопоставить такое множество: $U=\<1,2,3,4,5,6\>$. Представьте, что мы наугад запускаем руку в корзинку с целью вытащить три конфеты. Вытащенные конфеты – это и есть выборка. Так как мы вытаскиваем 3 конфеты из 6, то получаем (6,3)-выборку. Порядок расположения конфет в ладони совершенно несущественен, поэтому эта выборка является неупорядоченной. Ну, и так как все конфеты различны, то выборка без повторений. Итак, в данной ситуации говорим о неупорядоченной (6,3)-выборке без повторений.

Теперь подойдём с иной стороны. Представим себе, что мы находимся на фабрике по производству конфет, и на этой фабрике производятся конфеты четырёх сортов. Множество $U$ в этой ситуации таково: $U=\<1,2,3,4 \>$ (каждая цифра отвечает за свой сорт конфет). Теперь вообразим, что все конфеты ссыпаются в единый жёлоб, около которого мы и стоим. И, подставив ладони, из этого потока отбираем 20 конфет. Конфеты в горсти – это и есть выборка. Играет ли роль порядок расположения конфет в горсти? Естественно, нет, поэтому выборка неупорядоченная. Всего 4 сорта конфет, а мы отбираем двадцать штук из общего потока – повторения сортов неизбежны. При этом выборки могут быть самыми различными: у нас даже могут оказаться все конфеты одного сорта. Следовательно, в этой ситуации мы имеем дело с неупорядоченной (4,20)-выборкой с повторениями.

Рассмотрим ещё пару примеров. Пусть на кубиках написаны различные 7 букв: к, о, н, ф, е, т, а. Эти буквы образуют множество $U=\<к,о,н,ф,е,т,а\>$. Допустим, из данных кубиков мы хотим составить «слова» из 5 букв. Буквы этих слов (к примеру, «конфе», «тенко» и так далее) образуют (7,5)-выборки: $(к,о,н,ф,е)$, $(т,е,н,к,о)$ и т.д. Очевидно, что порядок следования букв в такой выборке важен. Например, слова «нокфт» и «кфтон» различны (хотя состоят из одних и тех же букв), ибо в них не совпадает порядок букв. Повторений букв в таких «словах» нет, ибо в наличии только семь кубиков. Итак, набор букв каждого слова представляет собой упорядоченную (7,5)-выборку без повторений.

Еще один пример: мы составляем всевозможные восьмизначные числа из четырёх цифр 1, 5, 7, 8. Например, 11111111, 15518877, 88881111 и так далее. Множество $U$ таково: $U=\<1,5,7,8\>$. Цифры каждого составленного числа образуют (4,8)-выборку. Порядок следования цифр в числе важен, т.е. выборка упорядоченная. Повторения допускаются, поэтому здесь мы имеем дело с упорядоченной (4,8)-выборкой с повторениями.

Размещения без повторений из $n$ элементов по $k$

Так как элементы в рассматриваемой выборке повторяться не могут, то мы не можем отобрать в выборку больше элементов, чем есть в исходном множестве. Следовательно, для таких выборок верно неравенство: $n≥ k$. Количество размещений без повторений из $n$ элементов по $k$ определяется следующей формулой:

Запись «n!» (читается «эн факториал») обозначает произведение всех чисел от 1 до n, т.е.

$$ n!=1\cdot2\cdot 3\cdot \ldots\cdot n $$

По определению полагается, что $0!=1!=1$. Для примера найдём 5!:

$$ 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120. $$

Алфавит состоит из множества символов $E=\<+,*,0,1,f\>$. Определим количество таких трёхсимвольных слов в этом алфавите, которые не содержат повторяющихся букв.

Под трёхсимвольными словами будем понимать выражения вида «+*0» или «0f1». В множестве $E$ пять элементов, поэтому буквы трехсимвольных слов образуют (5,3)-выборки. Первый вопрос: эти выборки упорядочены или нет? Слова, которые отличаются лишь порядком букв, полагаются различными, поэтому порядок элементов в выборке важен. Значит, выборка является упорядоченной. Второй вопрос: допускаются повторения или нет? Ответ на этот вопрос даёт условие: слова не должны содержать повторяющихся букв. Подводим итоги: буквы каждого слова, удовлетворяющего условию задачи, образуют упорядоченную (5,3)-выборку без повторений. Иными словами, буквы каждого слова образуют размещение без повторений из 5 элементов по 3. Вот примеры таких размещений:

Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:

Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.

Размещения с повторениями из $n$ элементов по $k$

Количество размещений с повторениями из $n$ элементов по $k$ определяется следующей формулой:

Сколько пятизначных чисел можно составить из множества цифр $\<5,7,2\>$?

Из данного набора цифр можно составить пятизначные числа 55555, 75222 и так далее. Цифры каждого такого числа образуют (3,5)-выборку: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Зададимся вопросом: что это за выборки? Во-первых, цифры в числах могут повторяться, поэтому мы имеем дело с выборками с повторениями. Во-вторых, порядок расположения цифр в числе важен. Например, 27755 и 77255 – разные числа. Следовательно, мы имеем дело с упорядоченными (3,5)-выборками с повторениями. Общее количество таких выборок (т.е. общее количество искомых пятизначных чисел) найдём с помощью формулы (2):

Следовательно, из заданных цифр можно составить 243 пятизначных числа.

Перестановки без повторений из $n$ элементов

По сути, перестановка без повторений есть частный случай размещения без повторений, когда объём выборки равен мощности исходного множества. Количество перестановок без повторений из $n$ элементов определяется следующей формулой:

Эту формулу, кстати, легко получить, если учесть, что $P_n=A_^$. Тогда получим:

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Пусть первому мороженому соответствует цифра 1, второму – цифра 2 и так далее. Мы получим множество $U=\<1,2,3,4,5\>$, которое будет представлять содержимое морозилки. Порядок съедения может быть таким: $(2,1,3,5,4)$ или таким: $(5,4,3,1,2)$. Каждый подобный набор есть (5,5)-выборка. Она будет упорядоченной и без повторений. Иными словами, каждая такая выборка есть перестановка из 5 элементов исходного множества. Согласно формуле (3) общее количество этих перестановок таково:

Следовательно, существует 120 порядков выбора очередности съедения.

Перестановки с повторениями

Общее количество перестановок с повторениями определяется формулой:

Слова составляются на основе алфавита $U=\$. Сколько различных слов из семи символов может быть составлено, если в этих словах буква «a» должна повторяться 2 раза; буква «b» – 1 раз, а буква «d» – 4 раза?

Вот примеры искомых слов: «aabdddd», «daddabd» и так далее. Буквы каждого слова образуют (3,7)-выборку с повторениями: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d)$ и т.д. Каждая такая выборка состоит из двух элементов «a», одного элемента «b» и четырёх элементов «d». Иными словами, $k_1=2$, $k_2=1$, $k_3=4$. Общее количество повторений всех символов, естественно, равно объёму выборки, т.е. $k=k_1+k_2+k_3=7$. Подставляя эти данные в формулу (4), будем иметь:

Следовательно, общее количество искомых слов равно 105.

Сочетания без повторений из $n$ элементов по $k$

Общее количество сочетаний без повторений из $n$ элементов по $k$ определяется формулой:

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Итак, в данной задаче исходное множество таково: $U=\<1,2,3,4,5,6,7,8,9,10\>$. Из этого множества мы выбираем четыре элемента (т.е., четыре карточки из корзины). Номера вытащенных элементов образуют (10,4)-выборку. Повторения в этой выборке не допускаются, так как номера всех карточек различны. Вопрос вот в чём: порядок выбора карточек играет роль или нет? Т.е., к примеру, равны ли выборки $(1,2,7,10)$ и $(10,2,1,7)$ или не равны? Тут нужно обратиться к условию задачи. Карточки вынимаются для того, чтобы потом найти сумму элементов. А это значит, что порядок карточек не важен, так как от перемены мест слагаемых сумма не изменится. Например, выборке $(1,2,7,10)$ и выборке $(10,2,1,7)$ будет соответствовать одно и то же число $1+2+7+10=10+2+1+7=20$. Вывод: из условия задачи следует, что мы имеем дело с неупорядоченными выборками. Т.е. нам нужно найти общее количество неупорядоченных (10,4)-выборок без повторений. Иными словами, нам нужно найти количество сочетаний из 10 элементов по 4. Используем для этого формулу (5):

Следовательно, общее количество искомых наборов равно 210.

Сочетания с повторениями из $n$ элементов по $k$

Общее количество сочетаний с повторениями из $n$ элементов по $k$ определяется формулой:

Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных «конфетных комбинаций» может оказаться в горсти?

Если принять, что первому сорту соответствует число 1, второму сорту – число 2 и так далее, то исходное множество в нашей задаче таково: $U=\<1,2,3,4\>$. Из этого множества мы выбираем 20 элементов (т.е., те самые 20 конфет с конвейера). Пригоршня конфет образует (4,20)-выборку. Естественно, повторения сортов будут. Вопрос в том, играет роль порядок расположения элементов в выборке или нет? Из условия задачи следует, что порядок расположения элементов роли не играет. Нам нет разницы, будут ли в горсти располагаться сначала 15 леденцов, а потом 4 шоколадных конфеты, или сначала 4 шоколадных конфеты, а уж потом 15 леденцов. Итак, мы имеем дело с неупорядоченной (4,20) выборкой с повторениями. Чтобы найти общее количество этих выборок используем формулу (6):

Следовательно, общее количество искомых комбинаций равно 1771.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник