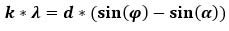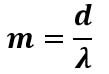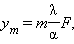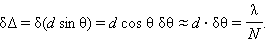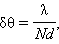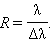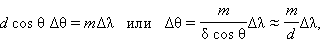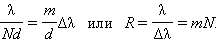Способы разложения немонохроматического света спектр

Ответы на любые вопросы

Школьный курс физики кажется совсем не сложным, понятным и достаточно интересным. Не так уж трудно объяснить на уроке учителю, чем отличается дифракционный спектр от дисперсионного, и получить хорошую оценку. Но когда речь идет о физике в высших учебных заведениях, все резко усложняется. Некоторые задачки могут заставить провести за их решением не одну бессонную ночь.

Разные способы разложения света на спектр

И дифракция и дисперсия представляют собой разложение светового луча на составляющие, но всегда есть свои нюансы:

Получается в результате контакта света и дифракционной решетки.

Можно добиться во время прохождения луча через призму.

Равномерно распространяется во всех направлениях.

Растянут в фиолетовом направлении, а в сторону красного – сжат.

Направление цветов в спектре идет от фиолетового цвета к красному.

Распространяется от красного к фиолетовому цвету.

Опыт с дисперсией многие видели на уроках физики. Для этого достаточно было направить луч на призму, рядом с которой находился простой альбомный лист. И обычный солнечный свет или направленный луч из фонарика раскладывался на все цвета радуги.

Но при этом, красный цвет занимал на листе совсем немного места, ширина остальных цветов увеличивалась, по направлению к фиолетовому. Именно он занимал значительную часть всего спектра.

Наибольший порядок спектра дифракционной решетки

Оптика это точная наука, которая требует логического мышления и верных расчетов. Некогда физики вывели формулу, которой мы можем пользоваться, по сей день:

В этом сложном, но только на первый взгляд, равенстве, искомой величиной является k – порядок спектра:

• λ – длина волны света, падающего на решетку.
• φ – угол дифракции.
• ά – угол падения на решетку световой волны.
• đ – период решетки.

Из этого равенства можно вывести интересующую нас формулу, для определения максимального порядка спектра. Для этого достаточно правую часть равенства поделить на длину световой волны, при этом синус угла дифракции можно заменить единицей, для простоты вычисления.

Часть из необходимых для вычисления величин – постоянная, так что никаких проблем возникнуть не должно. Главное, не запутаться в подсчетах.

Простой способ вычисления максимального порядка спектра

А еще у физиков есть более простой способ определения максимального порядка. Для формулы можно использовать значения из предыдущего равенства. Только в этот раз исходных данных будет гораздо меньше, а сами расчеты можно представить в виде:

Как несложно понять, искомое значение напрямую зависит от периода решетки и длины волны. Синусы мы благополучно откинули, а максимальный порядок выразили в виде m.

На деление двух чисел сложно потратить больше минуты, так что любая задача на оптику, в которой требуется лишь определить значение порядка, не займет так уж много времени. Но чаще всего это вычисление – только первый шаг на пути к поиску ответа на более сложный вопрос.

Если разобраться в вопросе и вникнуть в суть понятия, формула кажется предельно логичной. Проще всего решать задачу с белым светом, ведь в таком случае длина волны одинакова для всего светового потока.

А теперь представьте, что в потоке несколько оттенков, которые, конечно же, имеют разную длину. Задача несколько усложняется, на вычисления уйдет больше времени. А так уж вышло, в реальной жизни, что волны исключительно белого света встречаются крайне редко.

Ширина дифракционного спектра

На опыте с призмой вы могли понаблюдать за неоднородностью и шириной спектра. Этот параметр имеет огромное значение в оптике, особенно когда речь идет о дифракционном спектре. Дело в том, что в отличие от дисперсионного он не сжат ни в одном направлении, все оттенки представлены равномерно и ширина зависит только от показателей самой решетки, с помощью которой и проводится разложение луча на спектр. В то время как значения ширины дисперсионного спектра зависит от длины волны. В дифракционной решетке:

1. Есть прозрачные штрихи.
2. Есть непрозрачные промежутки.
3. Сумма их длин является периодом решетки.
4. Получить это значение можно поделив единицу на количество штрихов на единицу длины решетки.

Интересующая нас ширина спектра находится в обратной зависимости от периода решетки, который уже фигурировал в предыдущих формулах. Только теперь чем меньше этот период, тем больше ширина.

Если вернуться к определению максимального порядка, можно заметить, что с увеличением значения периода решетки возрастал и порядок. Из этого, чисто логически, несложно сделать еще один вывод – ширина дифракционного спектра и его максимальный порядок находятся в обратной взаимосвязи.

Разница между спектрами

Чтобы выделить различия дисперсионного и дифракционного спектра, необходимо понять, что каждый из них собой представляет.
Дисперсионный:

• Появляется в результате разложения луча света на составляющие, после прохождения через призму.
• Распространяется от красного цвета к фиолетовому.
• Спектр сжат в том же направлении, наименьшей шириной обладает красный диапазон, наибольшей – фиолетовый.
• Может существовать только одна цветная картинка.

• Получается в результате попадания света на дифракционную решетку.
• Идет в обратном порядке, от фиолетового к красному цвету.
• Спектр равномерен на всем своем протяжении.
• Может быть несколько цветных картинок.

Со знания, чем отличается дифракционный спектр от дисперсионного спектра, можно начать изучение оптики. Перспективы этой дисциплины недооценены, так что исследователей ждет гарантированная занятость в будущем, а может быть и серьезные открытия.

Видео: различия дифракционного и дисперсионного спектра

В этом видео ученый-физик Денис Логачев проведет урок, в котором расскажет об отличии дифракционного спектра от дисперсионного, мы узнаем, что такое дифракционная решетка:

Источник

Способы разложения немонохроматического света спектр

В состав видимого света входят монохроматические волны с различными значениями длин. В излучении нагретых тел (нить лампы накаливания) длины волн непрерывно заполняют весь диапазон видимого света. Такое излучение называется белым светом . Свет, испускаемый, например, газоразрядными лампами и многими другими источниками, содержит в своем составе отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн. Совокупность монохроматических компонент в излучении называется спектром . Белый свет имеет непрерывный спектр , излучение источников, в которых свет испускается атомами вещества, имеет дискретный спектр . Приборы, с помощью которых исследуются спектры излучения источников, называются спектральными приборами .

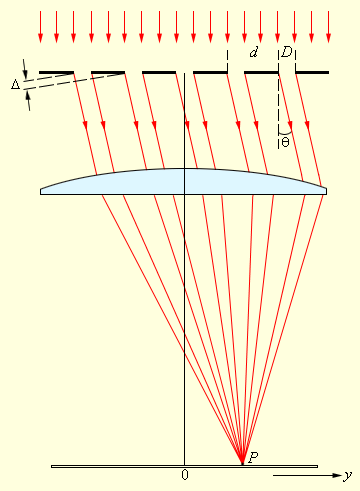
Для разложения излучения в спектр в простейшем спектральном приборе используется призма (рис. 3.10.1). Действие призмы основано на явлении дисперсии , то есть зависимости показателя преломления вещества от длины волны света .

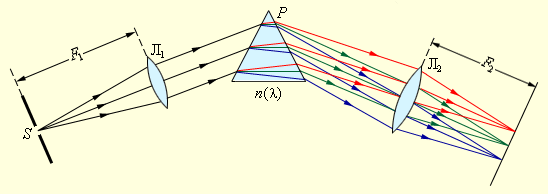Рисунок 3.10.1. Щель , на которую падает исследуемое излучение, находится в фокальной плоскости линзы . Эта часть прибора называется коллиматором . Выходящий из линзы параллельный пучок света падает на призму . Вследствие дисперсии свет разных длин волн выходит из призмы под разными углами. В фокальной плоскости линзы располагается экран или фотопластинка, на которой фокусируется излучение. В результате в разных местах экрана возникает изображение входной щели в свете разных длин волн. У всех прозрачных твердых веществ (стекло, кварц), из которых изготовляются призмы, показатель преломления в диапазоне видимого света убывает с увеличением длины волны , поэтому призма наиболее сильно отклоняет от первоначального направления синие и фиолетовые лучи и наименее – красные. Монотонно убывающая зависимость называется нормальной дисперсией . Первый опыт по разложению белого света в спектр был осуществлен И. Ньютоном (1672 г.). В спектральных приборах высокого класса вместо призм применяются дифракционные решетки . Решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки (рис. 3.10.2). У хороших решеток параллельные друг другу штрихи имеют длину порядка , а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки. Рисунок 3.10.2. Простейшая дифракционная решетка состоит из прозрачных участков (щелей), разделенных непрозрачными промежутками. На решетку с помощью коллиматора направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой (рис. 3.10.3). Рисунок 3.10.3. В каждой точке на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом к направлению падающей волны. Колебание в точке является результатом интерференции вторичных волн, приходящих в эту точку от разных щелей. Для того, чтобы в точке наблюдался интерференционный максимум, разность хода между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн: Здесь – период решетки, – целое число, которое называется порядком дифракционного максимума . В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины. В фокальной плоскости линзы расстояние от максимума нулевого порядка () до максимума -го порядка при малых углах дифракции равно где – фокусное расстояние. Следует обратить внимание на то, что в каждой точке фокальной плоскости линзы происходит интерференция волн, приходящих в эту точку от щелей решетки. Это так называемая многоволновая (или «многолучевая») интерференция. Распределение световой энергии в плоскости наблюдения резко отличается от того, которое получается в обычных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, потому амплитуда колебаний возрастает в раз, а интенсивность в раз по сравнению с колебанием, которое возбуждает волна только от одной щели. При смещении из главных максимумов интенсивность колебаний быстро спадает. Чтобы волн погасили друг друга, разность фаз должна измениться на , а не на π, как при интерференции двух волн. На рис. 3.10.4 изображена векторная диаграмма колебаний, возбуждаемых волнами от всех щелей при условии, что сдвиг фаз волн от соседних щелей равен , а соответствующая разность хода равна . Вектора, изображающие колебаний, образуют в этом случае замкнутый многоугольник. Таким образом, при переходе из главного максимума в соседний минимум разность хода должна измениться на . Из этого условия можно оценить угловую полуширину главных максимумов: Здесь для простоты полагается, что дифракционные углы достаточно малы. Следовательно, где – полный размер решетки. Это соотношение находится в полном согласии с теорией дифракции в параллельных лучах, согласно которой дифракционная расходимость параллельного пучка лучей равна отношению длины волны к поперечному размеру препятствия. Рисунок 3.10.4. Можно сделать важный вывод: при дифракции света на решетке главные максимумы чрезвычайно узки. Рис. 3.10.5 дает представление о том, как меняется острота главных максимумов при увеличении числа щелей решетки. Рисунок 3.10.5. Как следует из формулы дифракционной решетки, положение главных максимумов (кроме нулевого) зависит от длины волны . Поэтому решетка способна разлагать излучение в спектр, то есть она является спектральным прибором . Если на решетку падает немонохроматическое излучение, то в каждом порядке дифракции (т. е. при каждом значении ) возникает спектр исследуемого излучения, причем фиолетовая часть спектра располагается ближе к максимуму нулевого порядка. На рис. 3.10.6 изображены спектры различных порядков для белого света. Максимум нулевого порядка остается неокрашенным. Рисунок 3.10.6. С помощью дифракционной решетки можно производить очень точные измерения длины волны. Если период решетки известен, то определение длины сводится к измерению угла , соответствующего направлению на выбранную линию в спектре -го порядка. На практике обычно используются спектры 1-го или 2-го порядков. Если в спектре исследуемого излучения имеются две спектральные линии с длинами волн и , то решетка в каждом спектральном порядке (кроме ) может отделить одну волну от другой. Одной из важнейших характеристик дифракционной решетки является ее разрешающая способность , характеризующая возможность разделения с помощью данной решетки двух близких спектральных линий с длинами волн и . Спектральной разрешающей способностью называется отношение длины волны к минимальному возможному значению Δλ, то есть Разрешающая способность спектральных приборов, и, в частности, дифракционной решетки, также как и предельное разрешение оптических инструментов, создающих изображение объектов (телескоп, микроскоп) определяется волновой природой света. Принято считать, что две близкие линии в спектре -го порядка различимы, если главный максимум для длины волны отстоит от главного максимума для длины волны не менее, чем на полуширину главного максимума, т. е. на . По существу, это критерий Релея, примененный к спектральному прибору. Из формулы решетки следует: где – угловое расстояние между двумя главными максимумами в спектре -го порядка для двух близких спектральных линий с разницей длин волн . Для простоты здесь предполагается, что углы дифракции малы (). Приравнивая и , получаем оценку разрешающей силы решетки: Таким образом, предельное разрешение дифракционной решетки зависит только от порядка спектра и от числа периодов решетки . Пусть решетка имеет период , ее длина . Тогда, (это хорошая решетка). В спектре 2-го порядка разрешающая способность решетки оказывается равной . Это означает, что минимально разрешимый интервал длин волн в зеленой области спектра () равен . В этих же условиях предельное разрешение решетки с и оказалось бы равным . Источник Читайте также:  Геометрический способ задания множества Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты