Способы распространения выборочных данных на генеральную совокупность
Конечной целью любого выборочного наблюдения является распространение его характеристик на генеральную совокупность. Существует два способа распространения данных выборочного наблюдения на генеральную совокупность: способ прямого пересчета и способ поправочных коэффициентов. Способ прямого пересчета применяется в том случае, если целью выборочного наблюдения является определение объема признака генеральной совокупности, когда известна лишь численность ее единиц (пример 1). Способ поправочных коэффициентов применяется в тех случаях, когда целью выборочного метода является уточнение результатов сплошного наблюдения (пример 2).
Пример 1. Для определения качества продукции проверено 200 изделий из 10000, или 2%. В результате проверки установлено с вероятностью 0,997, что средний процент бракованной продукции выборочной партии составил 4%, а пределы возможных отклонений 
0,5%. Способом прямого пересчета необходимо определить количество бракованных изделий в генеральной совокупности.
Генеральная средняя будет находится в пределах:
Количество бракованных изделий во всей партии (штук):
Пример 2. При проведении сплошного учета скота в регионе было зарегистрировано 10000 голов. С целью проверки данных сплошного учета проведены контрольные обходы части обследованных хозяйств и выявлено, что если данные сплошного учета скота в хозяйствах, попавших в выборку, показали 300 голов, то данные выборки в этих же хозяйствах – 305 голов. Следовательно, «процент недоучета» (коэффициент) при сплошном наблюдении составил:
Количество голов скота необходимо умножить на этот коэффициент:
Это значит, что при сплошном учете было недоучтено 167 голов.
Малые выборки и их особенности
Малая выборка – это несплошное статистическое обследование, численность единиц которого не превышает 30.
Для определенного способа отбора единиц величина стандартной ошибки зависит от объема выборки и степени колеблемости изучаемого признака в генеральной совокупности. Причем, чем меньше объем выборки, тем большую величину стандартной ошибки следует ожидать, а это снижает точность оценки параметров генеральной совокупности.
Для оценки возможных пределов ошибки малой выборки применяется отношение Стьюдента, определяемое по формуле:
,
где 
– величина среднего квадратического отклонения малой выборки, которая определяется по формуле:
Величина 
вычисляется на основе данных выборочного наблюдения. Она равна:
Таким образом, теоретическое распределение отношения Стьюдента t имеет дело с величинами, определяемыми непосредственно по данным выборки. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, которые приводятся в учебниках по математической статистике.
Предельная ошибка малой выборки определяется по формуле: 
Порядок расчетов тот же, что и при больших выборках.
Контрольные вопросы для самоподготовки:
1. Сущность, условия применения и способы отбора. Ошибки выборочного наблюдения (средняя и предельная), методы их расчета.
2. Виды и способы выборки. Определение доверительных границ обобщающих характеристик генеральной совокупности.
3. Малая выборка, ее специфика.
4. Определение необходимой численности выборки.
5. Способы распространения выборочных данных на генеральную совокупность.
Список использованной литературы
1. Федеральный закон «Об официальном статистическом учете и системе государственной статистики в Российской Федерации» от 29 ноября 2007 года № 282-ФЗ.
2. Приказ Ростехрегулирования №329-ст от 22 ноября 2007 г. «О внедрении Общероссийского классификатора продукции по видам экономической деятельности (ОКПД)»
3. Федеральная целевая программа Развитие государственной статистики России в 2007-2011 годах.
4. Методологические положения по статистике. — М.: Росстат 2006 — Вып.5.
1. Статистика: Учебно-практич. пособие / Под. ред. М.Г. Назарова.- М.:КНОРУС,2006*;
2. Социально-экономическая статистика. Практикум / под ред. С.А. Орехова. – М.: Эксмо, 2007. – 384 с.*
1. Теория статистики: Учебник / Под ред. Р.А. Шмойловой.-5-е изд.- М.: Финансы и статистика, 2005;*
2. Практикум по теории статистики. Учебное пособие. /Под ред. Шмойловой Р.А. — М.: Финансы и статистика, 2002*;
3. Статистика финансов: Учеб. Пособие / под ред.М.Г. Назарова. – М: Омега-Л, 2005. – 380 с.*
4. Статистика: Учебник / Под ред. В.Г. Ионина.-3-е изд., перераб. и доп.-М.: ИНФРА-М, 2006*
1. Статистика: Учебник / Под ред. И.И. Елисеевой.-М.: Высшее образование, 2006*;
2. Гусаров В.М. Статистика: Учеб. пособие для вузов. — М: ЮНИТИ-ДАНА, 2001*;
3. Статистика: Учебник / Под ред. B.C. Мхитаряна.-М.: Экономистъ, 2005*;
4. Статистика: Учеб.пособие / Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005*;
5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. — М.: Финансы и статистика, 2006*;
6. Журнал «Вопросы статистики».
Публикации в периодических изданиях
1. Божко В.П. Совершенствование процесса сбора первичных статистических данных в территориальных органах Росстата/ Божко В.П., Тульчинский Б.М. //Вопросы статистики. 2009. № 4. С.68-75.*
2. Лайкам К.Э. Основные итоги и направления развития государственной статистики / Лайкам К.Э. //Вопросы статистики. 2009. № 3. С.30-33.*
3. Пашинцева Н.И. Внедрение территориальными органами Росстата Административного регламента исполнения Федеральной службой государственной статистики государственной функции по предоставлению официальной статистической информации /Пашинцева Н.И. //Вопросы статистики. 2009. № 1. С.3-5.*
Источник
Способы распространения данных выборочного наблюдения
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборочной совокупности. Существуют два способа распространения данных выборочного наблюдения на генеральную совокупность – способ прямого пересчета и способ поправочных коэффициентов.
Способ прямого перерасчета заключается в том, что выборочная средняя или доля умножаются на численность генеральной совокупности и получается соответствующий объемный показатель. Так, в статистике сельского хозяйства выход шерсти от овец, находящихся в личном пользовании, определяется путем умножения полученных по выборке данных о среднем настриге шерсти с одной овцы на всю численность овец, находящихся в личной собственности. Например, согласно выборке, в области годовой настриг шерсти с одной овцы составляет 3 кг (с ошибкой выборки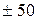 
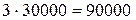
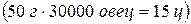
г), среднегодовая численность овец в хозяйствах – 30 тыс голов. Исходя из этого годовой выход шерсти в хозяйствах определяется как произведение настрига с одной овцы на все поголовье овец: 
кг, или 900 ц; с учетом ошибки выборки 
– от 885 до 915 ц.
Второй пример. в 3%-ной выборке численностью 150 светильников 6 светильников оказались бракованными (ошибка выборки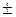 
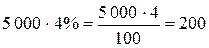
1 светильник). По количеству брака, имеющемуся в выборочной совокупности (4%), можно подсчитать, сколько брака будет во всей партии светильников, составляющей 5 000 шт. Брак составит:
светильников.
Данный способ применяется тогда, когда известна численность единиц в генеральной совокупности.
Способ поправочных коэффициентом используется при проведении контрольных выборочных наблюдений для проверки и уточнения данных сплошного наблюдения. Он заключается в том, что по одним и тем же объектам сопоставляют данные сплошного и контрольного выборочного наблюдения. В результате такого сопоставления исчисляют поправочные коэффициенты, которые применяют для внесения поправок в данные сплошных наблюдений. Поправочные коэффициенты исчисляют, например, на основе данных контрольных выборочных обследований скота, находящегося в личной собственности населения сельской местности, при контроле за качеством деталей непосредственно на рабочем месте и т.д.
Например, по данным сплошного наблюдения численность крупного рогатого скота в личном подсобном хозяйстве граждан составляет 1 0000 голов.
Для контрольной проверки отобрано 1 000 семей, в хозяйствах которых сплошным наблюдением определена численность поголовья скота 1000 голов. В результате контрольного обхода в этих хозяйствах установлена численность крупного рогатого скота 1 050 голов.
Отсюда поправочный коэффициент составляет 1 050:1 000=1,05.
Общее поголовье скота в личном подсобном хозяйстве граждан равно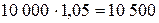 
голов.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Способы распространения выборочных результатов на генеральную совокупность. Предельная ошибка выборки
Выборочное наблюдение
Определение выборочного наблюдения
Виды и схемы отбора
Ошибки выборки
Способы распространения выборочных результатов на генеральную совокупность
Определение необходимого объема выборки
Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.
Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности по обследованной ее части.
Выборочное наблюдение– это метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются только по отдельно взятой части на основе положений случайного отбора.
При выборочном методе изучению подвергается только некоторая часть изучаемой совокупности, при этом подлежащая изучению статистическая совокупность называется генеральной совокупностью.
Выборочной совокупностью или просто выборкой можно называть отобранную из генеральной совокупности часть единиц, которая будет подвергаться статистическому исследованию.
Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда.
Если в период обследования будут соблюдены все правила его научной организации, то выборочный метод даст довольно точные результаты, и поэтому данный метод целесообразно применять для проверки данных сплошного наблюдения.
Этот метод получил широкое распространение в государственной и вневедомственной статистике, потому что при исследовании минимальной численности изучаемых единиц позволяет тщательно и точно провести исследование.
Изучаемая статистическая совокупность состоит из единиц с варьирующими признаками. Состав выборочной совокупности может отличаться от состава генеральной совокупности, это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки.
Ошибки, свойственные выборочному наблюдению, характеризуют размер расхождения между данными выборочного наблюдения и всей совокупности. Ошибки, возникающие в ходе выборочного наблюдения, называются ошибками репрезентативности и делятся на случайные и систематические.
Если выборочная совокупность недостаточно точно воспроизводит всю совокупность из–за несплошного характера наблюдения, то это называют случайными ошибками, и их размеры определяются с достаточной точностью на основании закона больших чисел и теории вероятностей.
Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения.
Виды и схемы отбора или формирования выборки
Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.
Различают четыре вида отбора совокупности единиц наблюдения:
4) серийный (гнездовой).
1. Случайный отбор– наиболее распространенный способ отбора в случайной выборке, его еще называют методом жеребьевки, при нем на каждую единицу статистической совокупности заготовляется билет с порядковым номером.
Далее в случайном порядке отбирается необходимое количество единиц статистической совокупности. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку, например тиражи выигрышей, когда из общего количества выпущенных билетов в случайном порядке наугад отбирается определенная часть номеров, на которые приходятся выигрыши. При этом всем номерам обеспечивается равная возможность попасть в выборку.
2. Механический отбор– это способ, когда вся совокупность разбивается на однородные по объему группы по случайному признаку, потом из каждой группы берется только одна единица. Все единицы изучаемой статистической совокупности предварительно располагаются в определенном порядке, но в зависимости от объема выборки механически через определенный интервал отбирается необходимое количество единиц.
3. Типический отбор –это способ, при котором исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности.
Типический отбор дает более точные результаты, так как при нем в выборку попадают представители всех типических групп.
4. Серийный (гнездовой) отбор.Отбору подлежат целые группы (серии, гнезда), отобранные случайным или механическим способом. По каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.
Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.
Повторный отбор.Каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку. Это так называемая схема возвращенного шара.
Бесповторный отбор.Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Эта схема получила название невозвращенного шара.
Бесповторный отбор дает более точные результаты, потому что при одном и том же объеме выборки наблюдение охватывает большее количество единиц изучаемой совокупности.
Комбинированный отборможет проходить одну или несколько ступеней. Выборка называется одноступенчатой, если отобранные однажды единицы совокупности подвергаются изучению.
Выборка называется многоступенчатой, если отбор совокупности проходит по ступеням, последовательным стадиям, причем каждая ступень, стадия отбора имеет свою единицу отбора.
Многофазная выборка – на всех ступенях выборки сохраняется одна и та же единица отбора, но проводится несколько стадий, фаз выборочных обследований, которые различаются между собой широтой программы обследования и объемом выборки.
Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.
Ошибки выборки
В статистике приняты следующие условные обозначения.
Доля выборки– это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
,
где N – объем генеральной совокупности;
n – объем выборки.
Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):
Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.
В генеральной совокупности доля единиц, которая обладает изучаемым признаком, называется генеральной долей (обозначается р),а средняя величина изучаемого варьирующего признака – это генеральная средняя (обозначается 
).
Основной задачей при выборочном исследовании является определение ошибок выборки. Ошибка выборки присуща только выборочным наблюдениям.
Для характеристики надежности выборочных показателей различаютпредельную и среднюю ошибки выборки.
Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.
Рассмотрим ошибки при 4-х видах отбора.
1. Собственно-случайная выборка– это отбор единиц из всей генеральной совокупности посредством жеребьевки (например, розыгрыш лотерей) или другим подобным способом (например, по таблице случайных чисел).
Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.
Собственно-случайный отбор в чистом виде в практике выборочного наблюдения встречается редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.
Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.
Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией s 2 . Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.
При случайном повторном отборе средние ошибки рассчитывают по следующим формулам:
1) для средней количественного признака:
где s 2 г – средняя величина генеральной дисперсии количественного признака.
2) для доли (альтернативного признака):
В эти формулы входит дисперсия признака в генеральной совокупности. Практически генеральная дисперсия точно не известна, но в теории вероятности 
доказано, что
,
где s 2 г – генеральная дисперсия (дисперсия признака в генеральной совокупности);
s 2 в – выборочная дисперсия того же признака;
Так как величина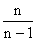 
при достаточно больших n близка к 1, можно считать, что 
. Тогда средняя ошибка выборки может быть рассчитана:
.
Но в случаях малой выборки (при n 2
С вероятностью не ниже 95 % определить
1. Границы, в которых находится среднее время
2. Границы, в которых находится доля студентов более 15 часов работающих за компьютером
Решение:
Среднее время / границы могут быть определены
1. 
, 
час
, где t = 2– коэффициент доверия
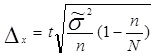
n = 900 человек (15 %) – объем выборки
N = 6000 человек (100%)– объем генеральной совокупности
= 
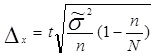
час 2
= 2 
ч
= (18 ±0,5) ч 17,5 – 18,5
2. 
, w = 
(60 %)
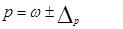
sр 2 = рq = 0,6 х 0,4 = 0,24
= 
(3 %)
= 60 ± 3, 57 — 63
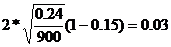
Дата добавления: 2018-02-28 ; просмотров: 2439 ; Мы поможем в написании вашей работы!
Источник
