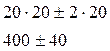Методы распространения выборочного наблюдения на генеральную совокупность
Основными методами распространения выборочного наблюдения на генеральную совокупность являются прямой пересчет и способ коэффициентов.
Прямой пересчет есть произведение среднего значения признака на объем генеральной совокупности. Однако большое число факторов не позволяет в полной мере использовать точечную оценку прямого пересчета при распространении результатов выборки на генеральную совокупность. На практике чаще пользуются интервальной оценкой, которая дает возможность учитывать размер предельной ошибки выборки, которая рассчитана для средней или для доли признака.
Способ коэффициентов используется в тех случаях, когда выборочное наблюдение проводится для проверки и уточнения данных сплошного наблюдения.
При этом рекомендуется использовать формулу
(11.20)
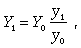
где Y1— численность совокупности с поправкой на недоучет; Y0— численность совокупности без этой поправки; y0— численность совокупности в контрольных точках по первоначальным данным; y1— численность совокупности в тех же точках по данным контрольных мероприятий.
Если нужно уточнить данные сплошного наблюдения при осуществлении контроля за выборочными исследованиями, необходимо определить поправку на недоучет. Метод расчета этой поправки широко применяется при исследовании небольших совокупностей, когда можно рассчитать коэффициент недоучета по каждой категории работников и, уточнив данные, распространить результаты на всю совокупность.
Пример: при проведении сплошного учета гаражей-ракушек в городе было зарегистрировано по южному (Ю) району 1000 гаражей; по северному (С) — 750; восточному (В) — 400. На основе контрольных выборочных мероприятий было установлено следующее количество гаражей, шт.:
| Район | p при учете | p в ходе контроля | Коэффициент недоучета |
| Ю С В | 200 150 100 | 210 160 110 | 1,050 1,066 1,100 |
Используя формулу способа коэффициентов (или используя рассчитанный коэффициент при выборочном учете), получаем численность гаражей после контроля (У) с поправкой на недоучет:
У(Ю) = 1000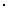 
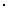
210 : 200 = 1050; У(С) = 750 160 : 150=800;
У(В) = 400 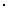110 : 100 = 440.
В итоге можно сказать, что на основе способа коэффициентов проверка результатов сплошного наблюдения широко применяется в социальной и экономической статистике, в частности в контроле за коммерческой деятельностью юридических и физических лиц со стороны финансовых организаций.
Источник
Способы распространения результатов выборки на генеральную совокупность
На заключительном этапе выборочного наблюдения решается вопрос о возможности распространения полученных результатов на генеральную совокупность. При этом учитываются два основных обстоятельства:
1). Насколько адекватно представлена генеральная совокупность в выборке, т. е. не изменилась ли в результате наблюдения структура запланированной её основы, соблюдены ли основные пропорции между типическими группами в выборочной и генеральной совокупности.
Для восстановления исходных пропорций генеральной совокупности проводится корректировка выборки либо путём отсечения части единиц, доля которых в выборке непропорционально велика по сравнению с долей в генеральной совокупности, либо путём многократного использования результатов наблюдения за единицами тех групп, которые недостаточно широко представлены в выборке.
2). Какова степень соответствия фактически полученной относительной ошибки выборки запланированному её уровню. Фактическое значение относительной ошибки определяется путём сопоставления абсолютной величины предельной ошибки выборки, полученной в результате исследования, со средним уровнем признака, рассчитанным на основе выборки.
Если выборка адекватна генеральной совокупности и фактическая относительная ошибка выборки незначительно отличается от запланированного её уровня, то на основе проведенного исследования можно оценить пределы, в которых находится среднее значение изучаемого признака (или доли) в генеральной совокупности, а также указать его возможное значение для совокупности в целом.
Общее значение изучаемого показателя для совокупности в целом определяется двумя способами: методом прямого пересчёта показателей выборки для генеральной совокупности или методом расчёта поправочных коэффициентов.
Способ прямого пересчёта состоит в том, что показатели выборочной доли w или выборочной средней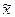 
распространяется на генеральную совокупность с учётом ошибки выборки.
Если в результате исследования получены верхняя и нижняя границы изучаемого признака в расчёте на единицу совокупности, т. е. найдены величины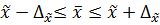 
, то с соответствующей вероятностью можно найти эти границы для совокупности в целом, умножив на N.
Так, в торговле определяется количество поступивших в партии товара нестандартных изделий. Для этого (с учётом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара.
При выборочном 3% обследовании качества продукции в выборку попало 1000 единиц, из которых качество 20 не соответствует стандарту. Ошибка выборки =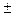 
2 единицы. Используя соотношение численности можно рассчитать, что число некачественных единиц из 20000 будет равно:
от 360 до 440 ед.
Способ поправочных коэффициентовприменяется для получения по данным выборки значений показателей, которые непосредственно не наблюдались, но тесно связаны с величинами, зафиксированными в ходе выборочного исследования, а также для уточнения данных сплошного наблюдения с помощью дополнительно проведённого выборочного исследования.
Сопоставляя выборочные данные с данными сплошного наблюдения, определяют поправочный коэффициент, а с его помощью вносят поправки в данные выборочной совокупности.
В статистической практике этот способ используется при уточнении данных ежегодных переписей скота, находящегося у населения. Для этого после обобщения данных сплошного учёта практикуется 10%-е выборочное исследование с определением так называемого «процента недоучёта».
Источник
Способы распространения результатов выборочного наблюдения на генеральную совокупность
Характеристики выборки могут быть распространены на генеральную совокупность с помощью одного из двух способов распространения выборочных данных:
— способа прямого пересчета;
— способа поправочных коэффициентов.
При первом способе средние величины и доли, полученные по выборке, переносятся на генеральную совокупность. При этом генеральная средняя определяется как 
, а генеральная доля – какР
.
Способ поправочных коэффициентов применяется, когда целью выборочного исследования является уточнение результатов сплошного наблюдения. Для этого после обобщения данных сплошного наблюдения практикуется 10%-ное выборочное наблюдение с установлением поправочного коэффициента 
, который устанавливает процент расхождений между данными сплошного и выборочного наблюдения.
Например, при проведении сплошного учета уличных торговых мест в городе их было зарегистрировано N=1000 шт. С целью уточнения данных через полгода был проведен контрольный обход части города и зарегистрировано 210 уличных торговых мест. По данным сплошного учета их было 200шт.
Необходимо уточнить число уличных торговых мест на новую дату: 
На новую дату число торговых мест составят 
Проверка статистических гипотез
Статистическая гипотеза – это гипотеза, которая допускает наблюдения статистической природы. Такие наблюдения могут возникать в различных областях деятельности человека. Вот некоторые примеры.
1) Вероятности выпадения каждой грани игральной кости равны. Это означает, что мы имеем равномерное распределение случайной переменной, которая представляет собой число точек на лицевой поверхности каждой грани данной кости.
2) Средняя длина детали, поступившей от нашего поставщика, больше, чем он заявлял (или меньше, или отличается от заявленной).
3) Средняя оценка стандартного тестирования у обучавшихся по новому методу выше, чем у обучавшихся по старому методу.
4) Значения параметров, характеризующих чистоту воздуха в городе, больше, чем установлено стандартом.
5) Для некоторых работодателей переменная «принятие на работу» не будет независимой от переменной «пол» (или «этническая принадлежность», «вероисповедание» и т. д.).
Из приведенных примеров следует, что статистическая гипотеза – это утверждение относительно характера или неизвестных параметров распределения случайных величин.
Гипотеза1 является гипотезой относительно абстрактной модели, вероятностном распределении случайной переменной, которая описывает игральную кость. Данная гипотеза может быть проверена с помощью наблюдений, например, 100 бросаний кости. Следующие три гипотезы касаются параметра. Они проверяются с помощью выборочных данных. Эти данные рассматриваются как выборочное распределение, необходимое для оценки параметра. Последняя гипотеза утверждает независимость двух качественных (нечисловых) переменных. Она проверяется путем сравнения наблюдаемых данных с истинными данными, ожидаемыми в случае независимости переменных. Отметим, что только три из пяти гипотез включает параметр, две другие представляют собой статистически утверждения другого рода.
Для каждого из этих примеров практически невозможно непосредственно определить истинность гипотезы. Например, вероятностное распределение для кости является моделью всех возможных бросаний, которые мы не можем наблюдать. Практически невозможно измерить длину каждой из сотен, а может быть и тысяч поступающих деталей. Для гипотезы (3) невозможно протестировать сегодня всех студентов, которые должны обучаться по новому методу в ближайшие 15 лет. Конечно, можно протестировать студентов через год после окончания обучения. Но оценку эффективности нового метода нужно делать до его реализации, а не после. А для гипотезы (4) можно ли проверить каждый кубический метр воздуха в городе? Наконец, что означает (5) прямая верификация для каждого человека?
Из-за невозможности определить истинность гипотезы прямым путем, мы «проверяем» гипотезу, т.е. устанавливаем, не противоречит ли высказанная нами гипотеза имеющимся выборочным данным. Эта процедура носит название статистической проверки гипотез.
Результат сопоставления высказанной гипотезы с выборочными данными может быть либо отрицательным (данные наблюдения противоречат высказанной гипотезе, а поэтому гипотезу надо отклонить), либо неотрицательным (данные наблюдения не противоречат высказанной гипотезе, а поэтому ее можно принять в качестве одного из возможных решений).
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Следовательно, эти гипотезы целесообразно различать.
Нулевая гипотеза (H0) – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияния фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Примером нулевой гипотезы является утверждение о том, что различие в результатах выполнения двумя группами учащихся одной и той же контрольной работы вызвано лишь случайными причинами.
Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Так, для упомянутого выше примера гипотезы Н0 одна из возможных альтернатив Н1 будет определена как: уровни выполнения работы в двух группах учащихся различны и это различие определяется влиянием неслучайных факторов, например, тех или других методов обучения.
С точки зрения статистической проверки гипотез существуют только два вида ошибок, называемые ошибкой I рода иошибкой II рода.
Ошибка I рода – это неправильное действие в соответствии с Н1: действовать в соответствии сН1, если справедливаН0, т.е. ошибочно отвергнуть нулевую гипотезу. Ошибка II рода – это неправильное действие в соответствии сН0: действовать в соответствии сН0, если справедливаН1. Вероятность ошибки интерпретируется как условная вероятность. Условные вероятности этих двух типов ошибок обозначаются соответственноα иβ:
α =Р (ошибка I рода) =Р (действие в соответствии сН1|Н0 истинна);
β =Р (ошибка II рода) =Р (действие в соответствии сН0|Н1 истинна).
В таблице 6.5 показаны возможности принятия решения и ошибки двух типов по отношению к гипотезе Н0. Отметим, что если гипотезаН0 справедлива и она принимается, то в таблице указано, что решение принято правильно. Если справедлива гипотезаН1, а принимаетсяН0 , то при решении допущена ошибка II рода. Если справедлива гипотезаН0 , а принимается гипотезаН1, то при решении допущена ошибка I рода.
Таблица 6.5 — Решения и ошибки при статистической проверке гипотез
Источник
