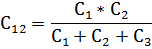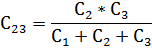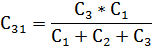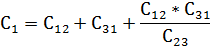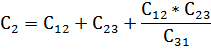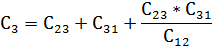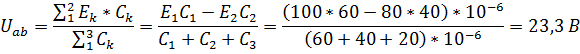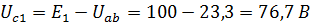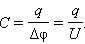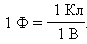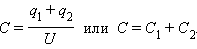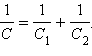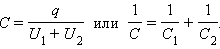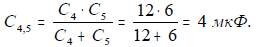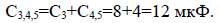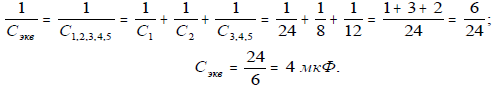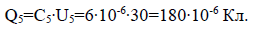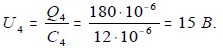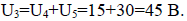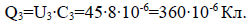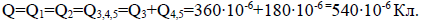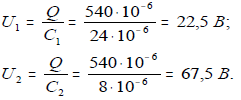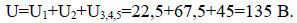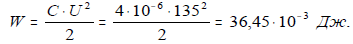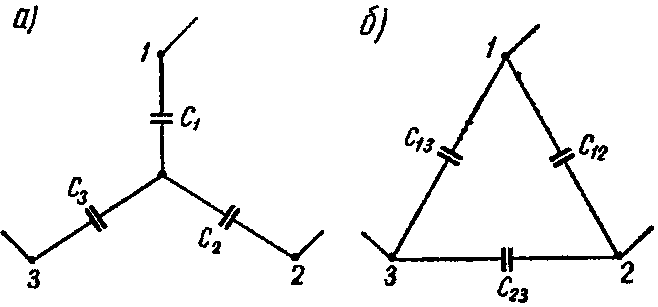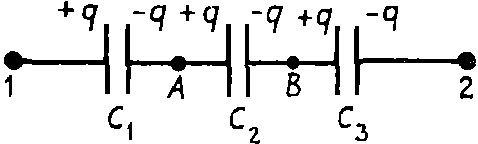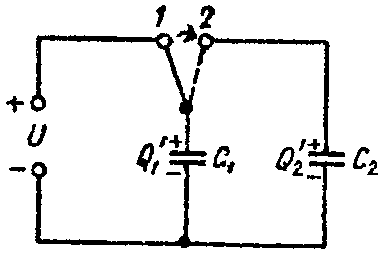Расчет электростатических цепей
Электростатической или емкостной называется электрическая цепь, состоящая
из конденсаторов и источников э.д.с. Расчет такой цепи состоит в определении напряжений и зарядов отдельных конденсаторов. Рассмотрим расчет емкостной цепи с идеальными конденсаторами (рис. 51). При постоянных э.д.с..токов в ветвях этой цепи не будет. Для емкостных цепей на основании электростатической аналогии получают зависимости, аналогичные законам Ома и Кирхгофа путем замены токов I на заряды Q и проводимостей g на емкости С,
Рис. 51
| Для цепей постоянного тока | Для элетростатических цепей |
| Закон Ома | |
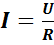 или I=U*g или I=U*g | Q=U*C |
| 1-й закон Кирхгофа | |
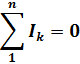 | 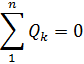 |
| 2-й закон Кирхгофа | |
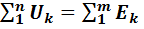 или или 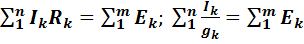 | 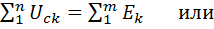 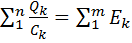 |
Для расчета электрических цепей можно применять все методы расчета цепей постоянного тока, если емкости конденсаторов постоянны. Удобнее применять метод узловых напряжений.
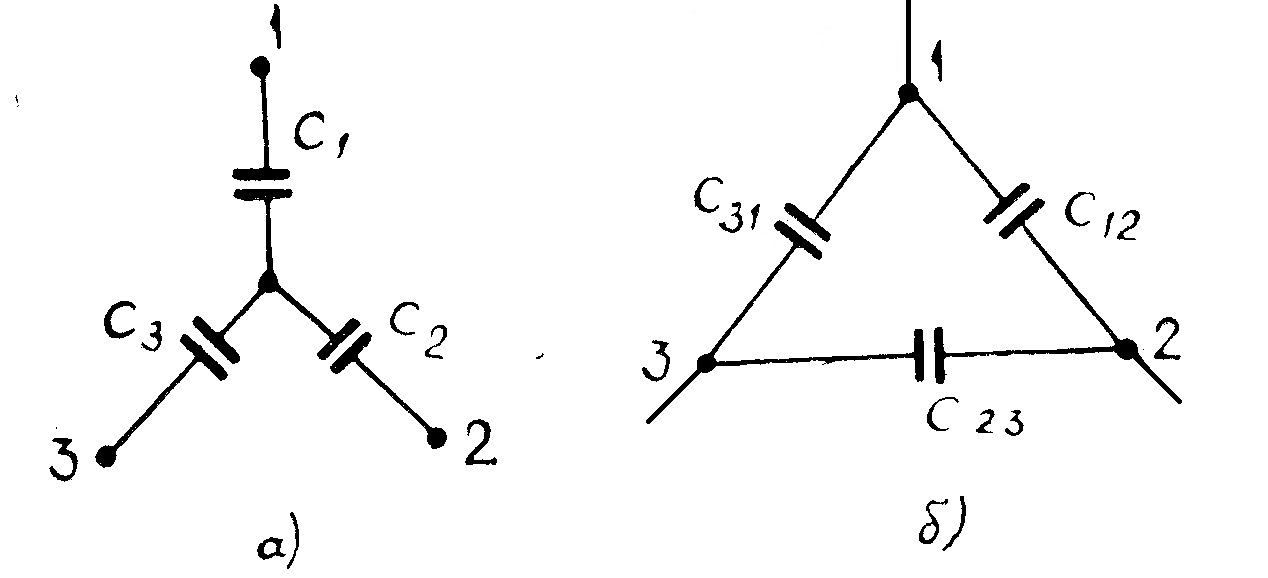
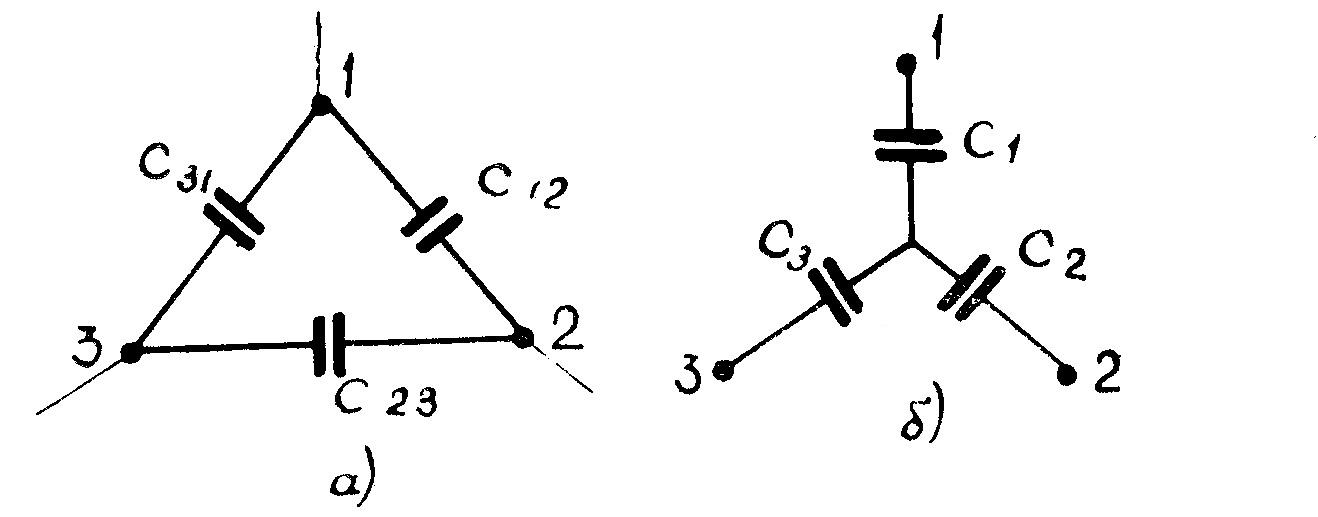
Для преобразования соединения конденсаторов звездой в соединение треугольником и обратно производится по формулам, аналогичным 2.21 и 2.22. Переход от звезды к треугольнику (рис. 52а, б):
Рис. 52
Переход от треугольника к звезде (рис. 53,а, б).
Рис. 53
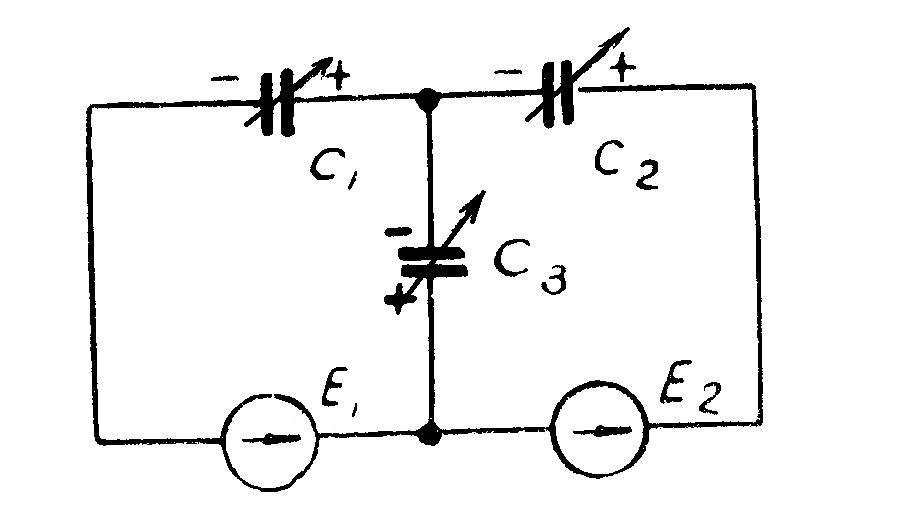
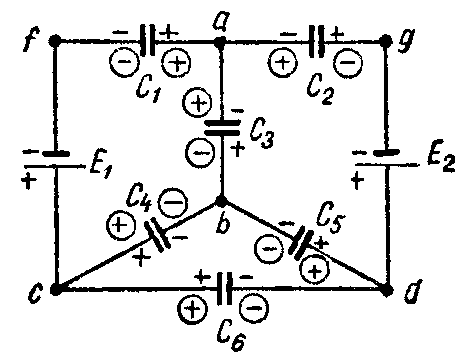
Пример 14. Определить напряжение на обкладках конденсаторов электрической цепи (рис. 54), если емкости конденсаторов 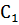
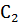
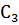
Решение: Зададим произвольно направления зарядов конденсаторов (направления напряжений на конденсаторах). Для расчета данной цепи применим метод двух узлов.
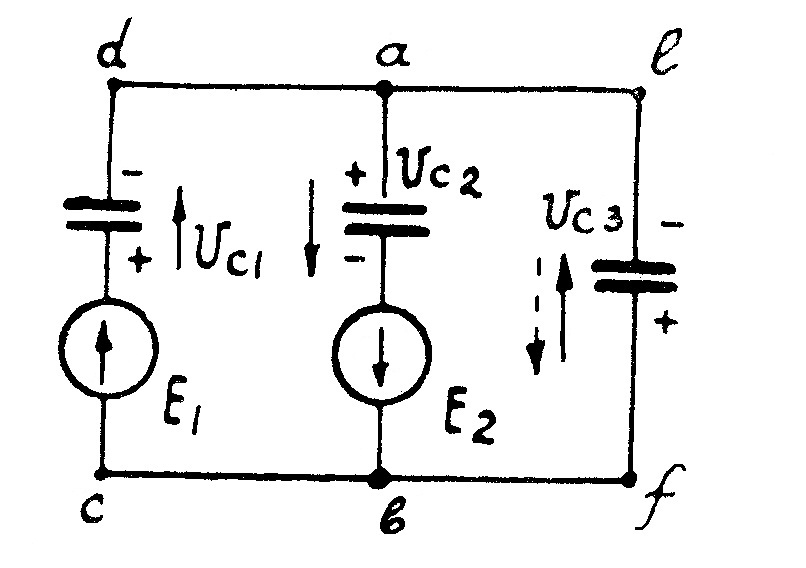
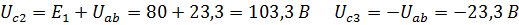
Проверка: по второму закону Кирхгофа для контура abcd:
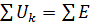
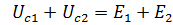
для контура abfe:
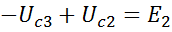
В отличие от идеальных, реальные конденсаторы имеют диэлектрик, обладающий хотя и большим, но конечным сопротивлением. Поэтому в цепях с конденсаторами при постоянных э.д.с. протекают токи, что в схемах учитывается включением параллельно конденсаторам сопротивлений утечки (рис: 55). Вследствие этого напряжения на конденсаторах распределяются в соответствии с сопротивлениями утечек вне зависимости от емкости конденсаторов. Заряды конденсаторов можно вычислить по известным значениям напряжений на конденсаторах и их емкостей.
Источник
Методика расчёта электрических цепей с конденсаторами.

Методика расчёта электрических цепей с конденсаторами.
Просмотр содержимого документа
«Методика расчёта электрических цепей с конденсаторами.»
Методика расчёта электрических цепей с конденсаторами.
Краткие теоретические сведения:
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад (Ф):
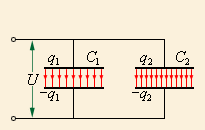
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2при напряжении между обкладками равном U. Отсюда следует
Таким образом, при параллельном соединении электроемкости складываются.
Параллельное соединение конденсаторов. C = C1 + C2
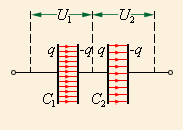
Последовательное соединение конденсаторов.
При последовательном соединении (рис.2.) одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них 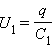
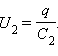
При последовательном соединении конденсаторов складываются обратные величины емкостей.
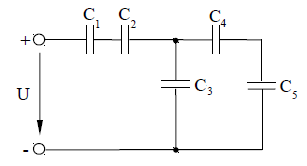
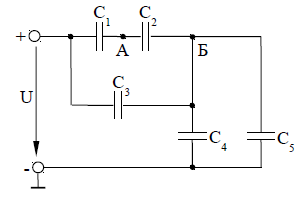
Пример расчёта:На рисунке 2 приведена схема соединения конденсаторов. Определить эквивалентнуюемкостьСэкв батареи конденсаторов, общий заряд Q, напряжение сети U, напряжение и заряд на каждом конденсаторе, если дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; напряжение на пятом конденсаторе U5=30 В.
Дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; U5=30 ВОпределить: U, Q, Сэкв, U1, U2, U3, U4, Q1.
Решение: 1. Общая емкость последовательно соединенных конденсаторов С4 и С5:
2. Общая емкость параллельно соединенных конденсаторов С3 иС4,5:
3. Общая емкость последовательно соединенных конденсаторов С1, С2 и С3,4,5, которая и является эквивалентной емкостью батареи конденсаторов:
4. По заданному напряжению U5 и емкости конденсатора С5 определяем заряд, накапливаемый этим конденсатором:
5. Заряд конденсатора С4 Q4=Q5=Q4,5=180・10 -6 Кл, т. к. конденсаторы С4 и С5 соединены последовательно. 6. Напряжение на четвертом конденсаторе:
7. Напряжение на третьем конденсаторе:
8. Заряд конденсатора С3:
9. Общий заряд батареи и заряды конденсаторов С1 и С2:
10. Напряжение на первом и втором конденсаторах:
11. Напряжение сети (напряжение последовательно соединенных конденсаторов С1, С2, С3,4,5):
12. Энергия электрического поля батареи:
На рисунке 4 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1.Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки.
Емкость конденсатора, мкФ
Точка, потенциал которой следует вычислить
Источник
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
2. Емкость плоского конденсатора
C = ε a ⋅ S d = ε r ⋅ ε 0 ⋅ S d ,
S – поверхность каждой пластины конденсатора;
d – расстояние между ними;
εr – диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4 π ⋅ с 2 ⋅ 10 − 7 ≈ 8,85418782 ⋅ 10 − 12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C = C 1 + C 2 + . + C n = ∑ k = 1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C = C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 = U ⋅ C 2 C 1 + C 2 ; U 2 = U ⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
осуществляется по формулам:
6. Энергия электростатического поля конденсатора:
W = C ⋅ U 2 2 = Q ⋅ U 2 = Q 2 2 C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k = 1 n E k = ∑ k = 1 n U C k = ∑ k = 1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 – φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 = ( φ 1 − φ A ) + ( φ A − φ B ) + ( φ B − φ 2 ) = U 1 A + U A B + U B 2 .
Воспользовавшись формулой напряжения на конденсаторе
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .
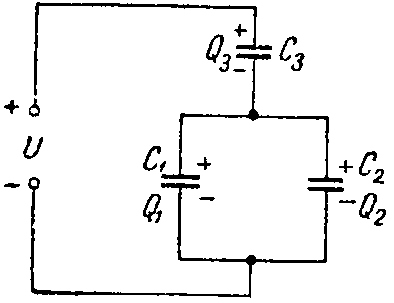
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
эквивалентная емкость всей цепи равна
C = C 12 ⋅ C 3 C 12 + C 3 = 200 ⋅ 300 500 = 120 м к Ф .
Заряд на эквивалентной емкости
Q = C·U = 120·10 –6 ·240 = 288·10 –4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10 –4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288 ⋅ 10 − 4 300 ⋅ 10 − 6 = 96 В .
Напряжение на конденсаторах C1 и C2 равно
их заряды имеют следующие значения
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72 ⋅ 10 − 4 ⋅ 144 2 ≈ 0,52 Д ж ; W 2 = Q 2 ⋅ U 2 2 = 216 ⋅ 10 − 4 ⋅ 144 2 ≈ 1,56 Д ж ; W 3 = Q 3 ⋅ U 3 2 = 288 ⋅ 10 − 4 ⋅ 96 2 ≈ 1,38 Д ж .
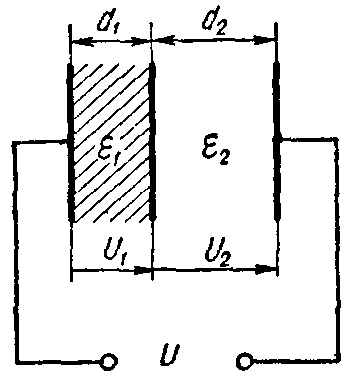
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см 2 , имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C = C 1 ⋅ C 2 C 1 + C 2 = ε a 1 ⋅ S d 1 ⋅ ε a 2 ⋅ S d 2 ε a 1 ⋅ S d 1 + ε a 2 ⋅ S d 2 = ε a 1 ⋅ ε a 2 ⋅ S ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 .
C = ε 0 ⋅ ε r 1 ⋅ ε r 2 ⋅ S ε r 1 ⋅ d 2 + ε r 2 ⋅ d 1 = 8,85 ⋅ 10 − 12 ⋅ 6 ⋅ 7 ⋅ 12 ⋅ 10 − 4 6 ⋅ 0,4 ⋅ 10 − 3 + 7 ⋅ 0,3 ⋅ 10 − 3 = 99 ⋅ 10 − 12 Ф .
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C ⋅ U п р ε a 1 ⋅ S d 1 = ε a 2 ⋅ d 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U п р ; U 2 = Q C 2 = C ⋅ U п р ε a 2 ⋅ S d 2 = ε a 1 ⋅ d 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U п р .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U ′ п р ; E 2 = U 2 d 2 = ε a 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U ″ п р .
Здесь U’np – общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»np – общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ п р = E 1 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 2 = 49,5 к В ; U ″ п р = E 2 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 1 = 27,0 к В .
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см 2 . Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅ S d 1 ⋅ U 2 2 ,
где С1 – емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из
где C2 – емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅ S d 2 ⋅ U 2 2 2 = ε 0 ⋅ S 10 d 1 ⋅ ( 10 U ) 2 2 = 10 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 10 ⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 = 9 ⋅ W 1 = 9 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 2,86 ⋅ 10 − 7 Д ж .
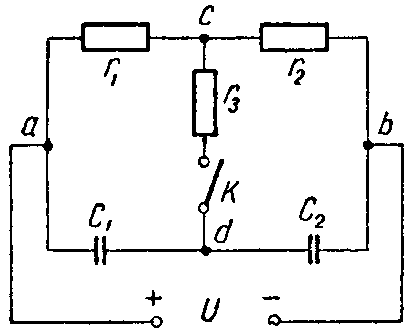
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅ U = 20 ⋅ 10 − 6 30 ⋅ 10 − 6 + 20 ⋅ 10 − 6 ⋅ 20 = 8 В ; U 2 = U − U 1 = 20 − 8 = 12 В .
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I = U r 1 + r 2 = 20 500 = 0,04 А ,
а через сопротивление r3 ток не протекает.
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
Аналогично напряжение на втором конденсаторе равно
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
По второму закону Кирхгофа имеем
0 = U C 1 − U C 2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
Q ′ 1 5 ⋅ 10 − 6 − Q ′ 2 120 ⋅ 10 − 6 = 0. ( 2 )
Решая уравнения (1) и (2), найдем
Напряжение на зажимах конденсаторов станет равным
U C 1 = Q ′ 1 C 1 = U C 2 = Q ′ 2 C 2 = 5 ⋅ 10 − 6 5 ⋅ 10 − 6 = 1 В .
Энергия обоих конденсаторов будет равна
W = C 1 ⋅ U C 1 2 2 + C 2 ⋅ U C 2 2 2 = 62,5 ⋅ 10 − 6 Д ж .
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W н а ч = C 1 ⋅ U 2 = 5 ⋅ 10 − 6 ⋅ 25 2 2 = 1562,5 ⋅ 10 − 6 Д ж .
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10 –6 – 62,5·10 –6 = 1500·10 –6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
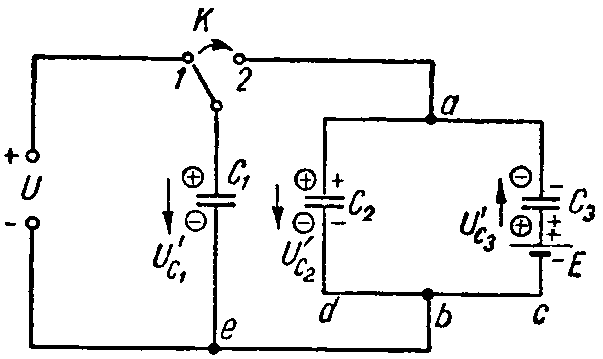
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
Рубильник находится в положении 1. Заряд конденсатора C1 равен
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E = U C 2 + U C 3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅ E = 30 ⋅ 10 − 6 ⋅ 60 ⋅ 10 − 6 90 ⋅ 10 − 6 ⋅ 50 = 1 ⋅ 10 − 3 К л .
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для контура 2ebda2
0 = U ′ C 1 − U ′ C 2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E = U ′ C 2 − U ′ C 3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) – (3), после подстановки числовых значений величин, примут вид
Решая совместно уравнения (4) – (6), получим
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C 1 = Q ′ 1 C 1 = 0,33 ⋅ 10 − 3 10 ⋅ 10 6 = 33 В ; U C 2 = Q ′ 2 C 2 = 0,99 ⋅ 10 − 3 30 ⋅ 10 6 = 33 В ; U C 3 = Q ′ 3 C 3 = 1,02 ⋅ 10 − 3 60 ⋅ 10 6 = 17 В .
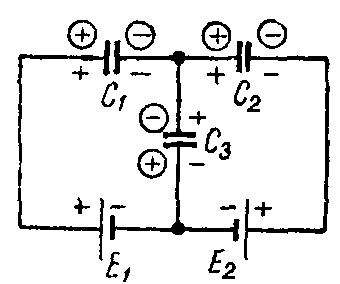
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 = 0 ; E 1 = U C 1 − U C 3 = Q 1 C 1 − Q 3 C 3 ; E 2 = − U C 2 − U C 3 = − Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 – противоположна выбранной.
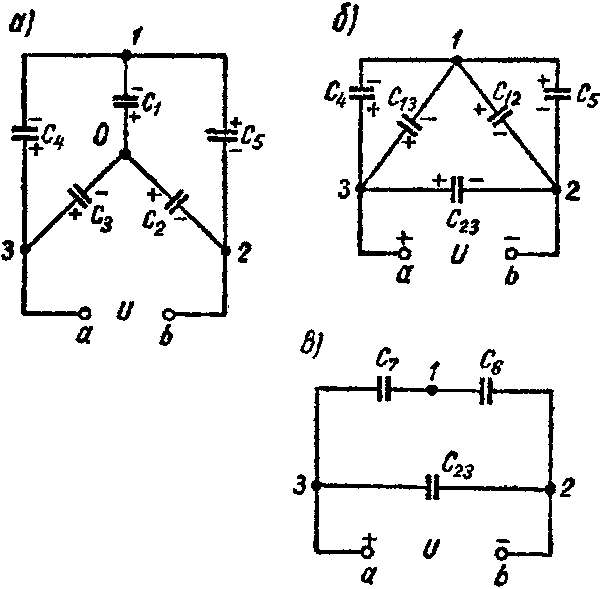
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 = 0,6 м к Ф ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 = 1,0 м к Ф ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 = 1,5 м к Ф .
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C a b = C 23 + C 6 ⋅ C 7 C 6 + C 7 = 2,7 м к Ф .
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅ U = 6 В .
Таково же напряжение и на конденсаторах C4 и C13
Напряжение на конденсаторе C6 равно
По закону сохранения электричества для узла 1 схем 8, а и б имеем
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 = 1,8 В .
Далее находим напряжения и заряды на остальных конденсаторах
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 = 0 ; ( 3 )
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 = 0 ; ( 4 )
Q 3 C 3 + Q 2 C 2 = U . ( 5 )
Система уравнений (1) – (5) – содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для контура afcba
E 1 = U C 1 + U C 4 − U C 3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C 5 − U C 3 + U C 2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0 = U C 4 − U C 5 − U C 6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
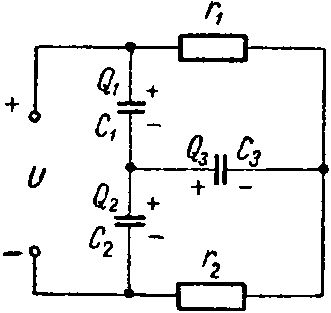
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
Через сопротивления протекает ток
I = U r 1 + r 2 = 0,05 А .
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 = 0 ; U = U C 1 + U C 2 = Q 1 C 1 + Q 2 C 2 ; I ⋅ r 1 = U C 1 + U C 3 = Q 1 C 1 + Q 3 C 3 ,
Q 1 = Q 2 + Q 3 ; 45 = Q 1 6 ⋅ 10 − 6 + Q 2 2 ⋅ 10 − 6 ; 25 = Q 1 6 ⋅ 10 − 6 + Q 3 3 ⋅ 10 − 6 .
Решив эту систему уравнений, найдем, что

Источник