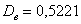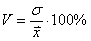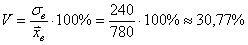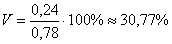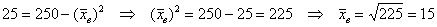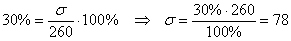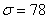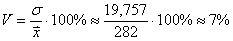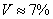Способы расчета среднего квадратического отклонения

Среднеквадратическое отклонение

Предлагаемая здесь программа, помимо расчета среднеквадратического отклонения, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.

Среднеквадратическое отклонение σ в строгом смысле является частным случаем стандартного отклонения S₀ (стандартной ошибки), хотя зачастую их уравнивают как синонимы, но в случае среднеквадратического отклонения мы имеем дело с отклонением от среднего арифметического [1] значения конечного набора величин, а в случае стандартного отклонения — с отклонением от математического ожидания некой (чаще всего случайной) величины.

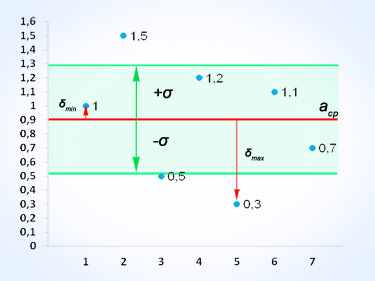
Среднеквадратическое отклонение значений множества заданных чисел от среднего арифметического определяется как число равное квадратному корню от суммы квадратов разности этих чисел и среднего арифметического, делённой на количество этих чисел:

В другом варианте определения можно сказать, что среднее квадратическое отклонение (стандартное отклонение) равно квадратному корню от дисперсии случайной величины [2] как меры разброса значений случайной величины относительно её математического ожидания.

Расчет среднеквадратического отклонения

Для начала расчета среднеквадратического отклонения введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному — они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:

Введите исходные данные

Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°

Среднеквадратическое отклонение, σ

Дисперсия [2] , σ 2

Среднее линейное отклонение [3] , δ

Коэффициент вариации [4] , V

Размах вариации [5] , R

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднеквадратического отклонения в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднеквадратического отклонения и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Страницы по теме «Расчет средних значений»

Свойства среднеквадратического отклонения

1. Среднее квадратическое отклонение имеет всегда положительную или равную нулю величину:

2. Среднее квадратическое отклонение для заданного множества неотрицательных чисел лежит между минимальным и максимальным значением линейного отклонения от среднего значения этого множества.

3. Кроме того квадратическое отклонение подчиняется неравенству о средних, то есть для любого множества чисел оно не меньше среднего линейного отклонения:

Прикладное значение среднеквадратического отклонения

Среднеквадратическое отклонение от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии, экспериментальной физике и статистике. При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение [3], [4] величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.

P.S. На этой странице используется Бета версия программы расчета среднеквадратического отклонения, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическое значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

3. Среднее линейное отклонение определяется как среднее от абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:

4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:

5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:

Источник

Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel

Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

Среднеквадратичное (стандартное) отклонение

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:

На практике формула стандартного отклонения следующая:

Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.

Расчет cреднеквадратичного (стандартного) отклонения в Excel

Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.

Коэффициент вариации

Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:

По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.

Расчет коэффициента вариации в Excel

Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:

Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Источник

6. Формула для вычисления дисперсии.
Среднее квадратическое отклонение. Коэффициент вариации

В первой части урока мы рассмотрели размах вариации, среднее линейное отклонение и дисперсию, и продолжение темы в заголовке. Многие из этих показателей фигурируют в теории вероятностей, и если вы зашли с поисковика именно за ними, то сразу ссылка на нужную статью: Дисперсия дискретной случайной величины – там же всё остальное.

Ну а здесь на повестке дня Математическая статистика (организационный урок для «чайников»), и мы продолжаем изучать показатели вариации:

Всё с формулами, примерами решений и техникой рациональных вычислений.

И снова о дисперсии.

На предыдущем занятии мы рассчитывали дисперсию по определению:
– для несгруппированных данных и
– для дискретного либо интервального вариационного ряда.

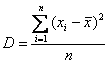
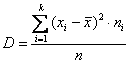
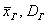
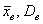
Если известно, генеральная ли нам дана совокупность или выборочная, то хорошим тоном считается поставить подстрочные индексы: либо .

Расчёт дисперсии по определению прост и реально используется на практике, но существует ещё более простой и удобный способ вычисления – по формуле, которую несложно вывести из определения:

– дисперсия равна разности средней арифметической квадратов всех вариант статистической совокупности и квадрата средней самих этих вариант.

ОСМЫСЛЕННО повторяем ВСЛУХ и вникаем! … Карл украл у Клары кораллы, а Клара украла у Карла кларнет 🙂

Если что-то не очень понятно, то сейчас всё станет на свои места:

Для несгруппированных вариант 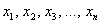выборочной совокупности формула детализируется следующим образом:

и для готового вариационного ряда – так: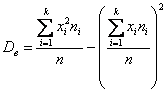
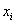
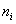
, где – кратные (одинаковые) варианты дискретного ряда либо середины интервалов интервального ряда, а – соответствующие частоты.

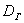
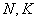
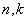
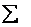
Для генеральной дисперсии формулы те же, только с буквами вместо . Во многих случаях удобно использовать просто значок суммирования – без переменной-«счётчика», поскольку в контексте той или иной задачи и так понятно, что суммируется.

И начнём мы со знакомой подопытной задачи:

В результате 10 независимых измерений получены опытные данные, которые представлены в таблице:

Это данные из Примера 13, и на этот раз нам требуется вычислить дисперсию с помощью формулы. Напоминаю, что там мы её рассчитали по определению и получили результат 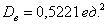, таким образом, ответ известен заранее, и это всегда круто. Всегда, когда он правильный.

Решение: используем формулу .
Для этого нужно найти выборочную среднюю, повторим действие: ,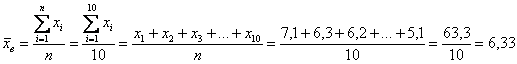
вычислить квадраты всех вариант: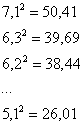

и их сумму: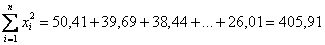
Результаты вычислений удобно заносить в таблицу: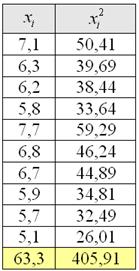

Осталось применить формулу: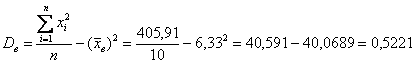
, что и требовалось увидеть.

Ответ:

Теперь случай сформированного вариационного ряда. В Примере 14 мы потренировались на дискретном ряде, и сейчас очередь интервального:

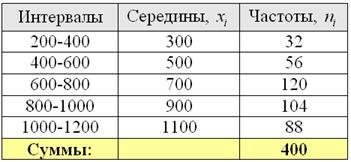
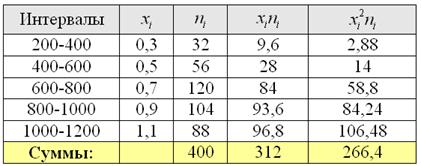
С целью изучения вкладов в Сбербанке города проведено выборочное исследование, в результате которого получены следующие данные: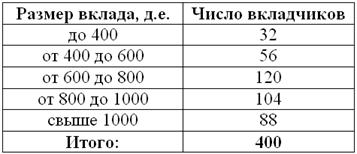

Вычислить выборочную дисперсию и среднее квадратическое отклонение, оценить соответствующие показатели генеральной совокупности.

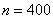
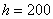
Автор задачи заботливо подсчитал объем выборки , но не «закрыл» крайние интервалы. Такая вещь уже встречалась, и решение мы начинаем с этого закрытия. Поскольку длины внутренних интервалов составляют д.е., то логично рассмотреть такую же длину и по краям, то бишь, интервалы от 200 до 400 и от 1000 до 1200 денежных единиц.

…Возможно, у вас возник вопрос, а как быть, если даны интервалы разной длины? В этом случае принимаем за «эталон» среднюю длину известных интервалов.

Для расчёта числовых характеристик перейдём к дискретному вариационному ряду, выбрав в качестве вариант 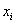середины интервалов, которые здесь видны устно:

В тяжёлых случаях суммируем концы интервалов и делим их пополам, например: .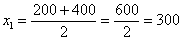

Кроме того, варианты целесообразно уменьшить в 1000 раз, поскольку в ходе дальнейших вычислений будут получаться гигантские числа. С современными вычислительными мощностями, это, конечно, не проблема, но смотреться будет некрасиво.

Сначала вычислим выборочную среднюю. Этот алгоритм уже обкатан: находим произведения 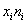, их сумму:

и по соответствующей формуле:
тыс. д.е. или 780 д.е. – средний размер вклада.

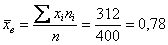
Примечание: далее для компактной записи я буду использовать просто значок – без переменной-«счётчика».

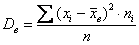
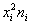
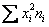
Теперь дисперсия. Её никто не запрещает рассчитать по определению , но заметьте, насколько легче формула – для её применения всего-то лишь нужно рассчитать произведения и их сумму (правый столбец таблицы). Несмотря на то, что многие читатели уже освоили технику вычислений в Экселе, я продолжу записывать ролики – мало ли, кто что запамятовал:

Итак, по формуле вычисления дисперсии, получаем:
тыс. д.е. в квадрате (т.к. по определению, дисперсия – есть величина квадратичная).

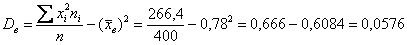
И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь квадратный корень:
тыс. д.е. или 240 денежных единиц. Полученный показатель называется

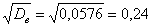
среднее квадратическое отклонение

Или стандартное отклонение. Оно обозначается греческой буквой «сигма», и коль скоро, у нас выборочная совокупность, то добавляем соответствующий подстрочный индекс:

– выборочное среднее квадратическое отклонение.

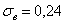
Чем меньше стандартное отклонение (и дисперсия), тем меньше вариация – тем бОльшее количество вариант находится вблизи выборочной средней. Но у нас, как нетрудно «прикинуть на глазок», разброс довольно-таки велик – значительное количество вкладов расположено далековато от 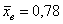, и поэтому значение получилось немалым.

Следующая часть задачи состоит в том, чтобы корректно оценить генеральную дисперсию и генеральное среднее квадратическое отклонение .

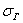
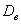
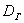
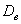
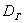
В 1-й части урока я рассказал о том, что выборочная дисперсия представляет собой смещённую оценку генеральной дисперсии. Это означает, что если мы будем проводить неоднократные выборки из той же генеральной совокупности, то полученные значения будут систематически занижено оценивать . Обращаю ваше внимание, что это не значит, что будет всегда меньше, чем .

И поэтому выборочную дисперсию, как намекает условие, нужно поправить:
– исправленная выборочная дисперсия

и, соответственно:
или 240,30 д.е. – исправленное среднее квадратическое отклонение.

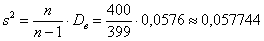
и – это уже несмещённые оценки генеральной дисперсии и генерального стандартного отклонения соответственно.

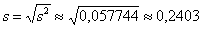
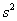
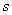
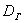
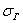
Ввиду большого объёма выборки (более 100 вариант) этой поправкой можно пренебречь, но всё же мы не будем «разбрасываться» 30 «копейками».

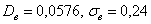
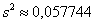
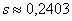
Ответ: ; в качестве оценки соответствующих генеральных показателей принимаем и .

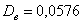
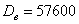
Рассмотренные выше показатели (размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение) входят в группу абсолютных показателей вариации, которые обладают рядом неудобств. Так, если в прорешанной задаче не уменьшать варианты в 1000 раз, то дисперсия получится в миллион раз больше! Да-да, не , а . И возникает естественное желание привести результаты к некому единому стандарту.

Для этого существуют показатели относительные, и самым известным из них является

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

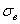
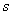
Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение 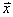хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество вариант находятся далеко от 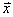, и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть квартили, децили, а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей 🙂

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов.

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке 🙂

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Решения и ответы:

Пример 17. Решение:

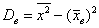
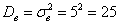
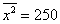
а) Используем формулу . По условию, , . Таким образом:

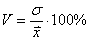
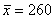
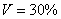
б) Используем формулу . По условию, , . Таким образом:

Ответ: а) 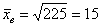, б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов: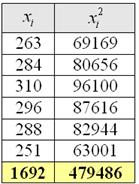

Найдём среднюю:
тонны – среднемесячный объем производства за полугодие.
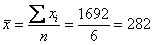
Дисперсию вычислим по формуле: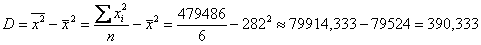

Среднее квадратическое отклонение:
тонн.
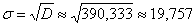
Коэффициент вариации:

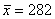
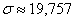
Ответ: тонны, тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил 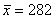тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник