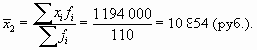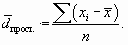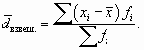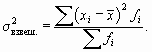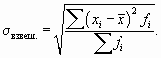Способы расчета показателей вариации статистика

Показатели вариации и способы их расчета

Понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называются факторами. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные (случайные), которые на одни единицы совокупности могут оказывать влияние, на другие нет.

Вариация, порождаемая существенными факторами, носит систематический характер, т.е. наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называется систематической. В систематической вариации проявляются взаимосвязи между явлениями, их признаками, в такой связи — один как причина (фактор), другой как следствие (результат) его действия. Точнее говоря, проявляется зависимость вариации одного признака от вариации другогоили от нескольких других.

Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.

Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации. Но систематическая вариация, если между признаками имеется довольно существенная связь, в конце концов пробивает себе дорогу через хаос случайных колебаний вариантов зависимого признака и проявляет себя.

Наличие вариации признаков, изучаемых статистикой явлений, ставит задачу определить меру вариации, ее измерение, найти соответствующие измерители — показатели, характеризующие размеры этой вариации, а также выявить сущность и методы вычисления определяющих ее факторов.

Показатели вариации и способы их расчета

Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. Исчислив среднюю арифметическую по данным вариационного ряда, мы не знаем о том, как отдельные значения изучаемого признака группируются вокруг средней. Для вариационного ряда важно изучать степень сплоченности всех отдельных значений признака вокруг его среднего значения, степень разбросанности этих значений, степень их колеблемости. Для этого в теории статистики используются показатели вариации.

Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. К относительным показателям вариации относятся: коэффициенты вариации, осцилляции, относительное линейное отклонение и др. Относительные показатели вычисляются как отношение абсолютных показателей вариации к средней величине.

1.Размах вариации (R)представляет собой разность между максимальным (x_max) и минимальным (x_min) значением признака исследуемой совокупности:

.

Размах вариации (амплитуда колебаний) дает лишь самое общее представление о размерах вариации, характеризует предел изменения значений признака в исследуемой совокупности. Этот показатель вариации обладает существенным недостатком: он характеризует только отклонения и не дает представление о распределении отклонений по все совокупности. Его величина определяется двумя крайними значениями признака, в то время как колеблемость последнего в целом складывается из всех его значений. Для анализа вариации необходим показатель, который бы отражал все колебания варьирующего признака и давал обобщенную его характеристику.

2. Среднее линейное отклонение ( 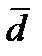)– это среднее из абсолютных отклонений значений признака от средней арифметической:

, .

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю.

Таково в среднем линейное отклонение вариантов признака от их средней величины. Если среднее линейное отклонение по сравнению со средней величиной признака небольшое, это свидетельствует о том, что данная совокупность в отношении нашего признака однородна, а средняя – типична. Таким образом, среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности.

3. Дисперсия – это среднее из квадратов отклонений индивидуальных значений признака от средней величины:

, .

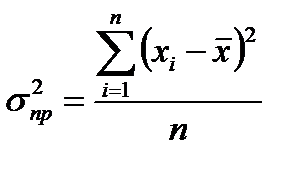
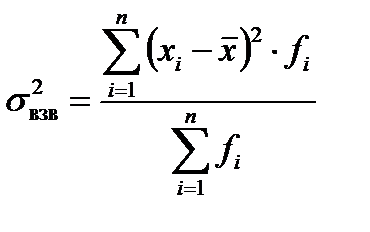
Математические свойства дисперсии

1) Дисперсия постоянной величины равна нулю:

.

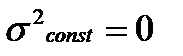
2) Дисперсия не изменится, если все значения признака увеличить или уменьшить на некоторую постоянную величину А.

.

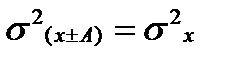
3) Если все значения варьирующего признака разделить (умножить) на одну и ту же величину h, то дисперсия уменьшится (увеличится) в h 2 раз.

, .

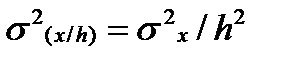
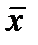
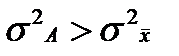
4)Средний квадрат отклонений индивидуальных значений признака от любой величины А, отличающейся от средней арифметической (A ≠ ), всегда больше среднего квадрата отклонений, исчисленного от средней арифметической:

или .

Средний квадрат отклонений при этом будет больше на вполне определенную величину – на квадрат разности средней от этой условно взятой величины А, т.е. на .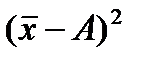

Другими словами, дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин.

или .

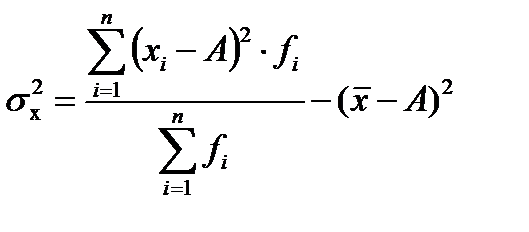
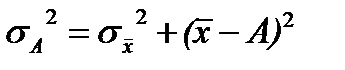
В случае когда А приравнивается нулю и, следовательно, отклонения не вычисляются, формула принимает следующий вид:

, или .

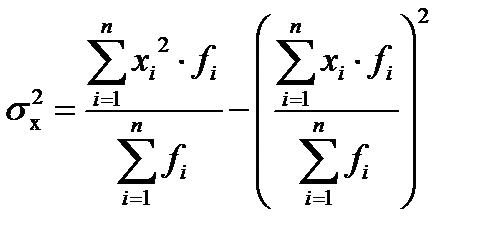
4.Среднее квадратическое отклонение находится как корень из дисперсии. Показывает (как и среднее линейное отклонение) на сколько в среднем индивидуальные значения признака отклоняются от средней арифметической:

, .

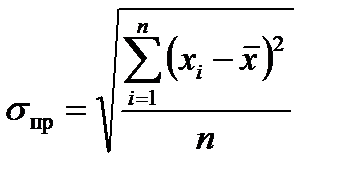
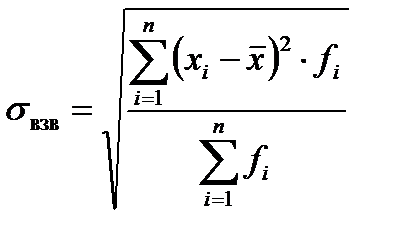
5.Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:

.

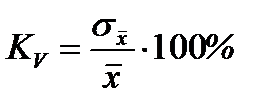
Считается, что если коэффициент вариации превышает 33%, то совокупность нельзя признать качественно однородной. Если K_v ≤ 33%, то можно утверждать, что совокупность более или менее однородна, а следовательно, средняя, рассчитанная по такой совокупности, типична. Необходимость исчисления коэффициента вариации вызвана тем, что показатели вариации в абсолютных величинах, как правило, непосредственно несравнимы.

Пример. Рассчитать показатели вариации по имеющимся данным (табл. 8.1).

Таблица 8.1 – Распределение предприятий по объему продаж

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе
1-5
5-9
9-13
13-17
17-21
ИТОГО

Алгоритм расчета показателей вариации следующий:

1) определим размах вариации:

R = 21 – 1 = 20 млн. руб.

2) найдем середину интервалов по исходным данным (x_i) и запишем в табл. 8.2;

3) определим среднее значение по формуле средней арифметической взвешенной, для этого введем графу (x_i f_i):

млн. руб.

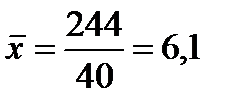
4) для расчета среднего линейного отклонения введем графы и :

млн. руб.

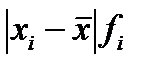
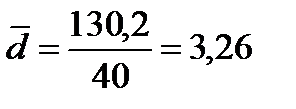
Таково в среднем отклонение вариантов признака от их средней величины.

5) для расчета дисперсии введем графы и :

.

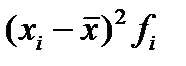
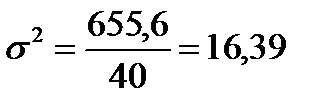
6) рассчитаем дисперсию упрощенным способом, для этого введем графу ( ):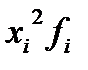

.

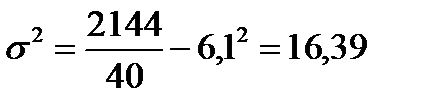
7) извлечем из дисперсии корень и получим среднее квадратическое отклонение:

млн. руб.

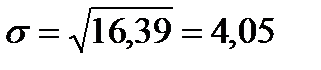
8) определим коэффициент вариации:

или 66%.

K_v > 33%, следовательно, изучаемая совокупность качественно неоднородна и рассчитанное среднее значение нетипично.

Таблица 8.2 – Расчет показателей вариации

Группа предприятий по объему продаж, млн.руб.	Число предприятий в группе, fi	Середина интервала, xi	xi fi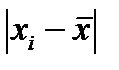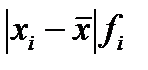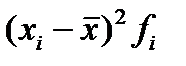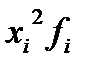
1-5	3,1	65,1	9,61	201,81
5-9	0,9	9,9	0,81	8,91
9-13	4,9	24,5	24,01	120,05
13-17	8,9	17,8	79,21	158,42
17-21	12,9	12,9	166,41	166,41
ИТОГО	—	—	130,2	—	655,6

Дата добавления: 2015-12-26 ; просмотров: 11310 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Показатели вариации в статистике

7.1. Абсолютные и относительные показатели вариации

Рассмотрим две совокупности сотрудников рекламных агентств.

Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1.

Таблица 7.1. Распределение сотрудников первого агентства по уровню месячной заработной платы

Размер месячной заработной платы, руб.	Середина интервала, xi	Число сотрудников, чел., fi	xi*fi
4 000-6 000	5 000	10	50 000
6 000-8 000	7 000	6	42 000
8 000-10 000	9 000	19	171 000
10 000-12 000	11 000	26	286 000
14 000-16 000	15 000	10	150 000
16 000-18 000	17 000	5	85 000
Сумма	—	95	1 031 000

Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2.

Таблица 7.2. Распределение сотрудников второго агентства по уровню месячной заработной платы

Размер месячной заработной платы, руб.	Середина интервала, xi	Число сотрудников, чел., fi	xi*fi
1 500-4 500	3 000	9	27 000
4 500-7 500	6 000	26	156 000
7 500-10 500	9 000	24	216 000
10 500-13 500	12 000	18	216 000
13 500-16 500	15 000	14	210 000
16 500-19 500	18 000	10	180 000
19 500-22 500	21 000	9	189 000
Сумма	—	110	1 194 000

Рассчитаем средний уровень заработной платы:

Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации.

Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации.

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия , среднее квадратическое отклонение.

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака

( 7.1)

Среднее линейное отклонение (d) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение

( 7.2)

Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:

( 7.3)

Дисперсией (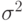) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней

( 7.4)

( 7.5)

Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением):

( 7.6)

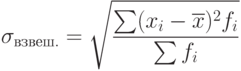( 7.7)

Абсолютные показатели вариации, за исключением дисперсии, имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Поэтому, если экономическая интерпретация , например, среднего линейного отклонения, проста и понятна физически, то в случае с дисперсией она затруднена. Однако дисперсия рассчитывается в статистическом анализе гораздо чаще, чем другие показатели вариации. Связано это с тем, что дисперсия широко используется в таких видах статистического анализа, как корреляционный, регрессионный, дисперсионный, при оценках результатов выборочного наблюдения. Кроме того, именно с помощью дисперсии можно оценить влияние случайных и систематических факторов на формирование значений случайной величины.

Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят:

Источник