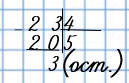Способы проверки деления с остатком

Деление с остатком

Начнём рассмотрение новой темы с решения задачи.

Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?

Каждый ребёнок получил по 4 конфеты.

На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?

Каждый получил по 2 конфеты и 2 конфеты остались лишними.

Как это записать?

Как сделать проверку?

Правило 1

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

Правило 2

При делении с остатком остаток всегда должен быть меньше делителя.

Порядок решения

1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.

2. Вычитаю из делимого найденное число: 14 − 10 = 4

3. Сравниваю остаток с делителем

Проверка деления с остатком

1. Умножаю неполное частное на делитель.

2. Прибавляю остаток к полученному результату.

3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.

Деление в столбик

В 23 содержится 5 раз по 4, и ещё остаётся 3.

Решение записывают так:

23 : 4 = 5 (ост. 3) или так:

, где 23 — делимое, 4 — делитель, 5 — неполное частное, а 3 — остаток.

Поделись с друзьями в социальных сетях:

Источник

Деление в столбик

О чем эта статья:

3 класс, 4 класс

Как правильно делить в столбик

Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.

Рассмотрим пример деления трехзначного числа на однозначное 322 : 7. Для начала определимся с терминами:

• 322 — делимое или то, что необходимо поделить;
• 7 — делитель или то, на что нужно поделить:
• частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.

Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза.

Проверяем: 4 × 7 = 28, а 28

Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся двойку и продолжаем размышлять.

Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.

Мы закончили решать пример и в результате получили целое число 46.

Как выглядит деление в столбик с остатком

Это такое же деление, только в результате получается неровное число, как получилось в примере выше.

• Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
• Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).

Примеры на деление в столбик

Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!

Источник

Деление чисел с остатком

О чем эта статья:

Деление с остатком целых положительных чисел

Деление — это разбиение целого на равные части.

Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.

Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!

Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.

Попрактикуемся в решении.

Пример

Разделить 14671 на 54.

Выполним деление столбиком:

Неполное частное равно 271, остаток — 37.

Ответ: 14671 : 54 = 271(остаток 37).

Деление с остатком положительного числа на целое отрицательное

Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:

В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.

Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.

Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».

Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.

Алгоритм деления положительного числа на целое отрицательное (с остатком):

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя
• получить неполное частное и остаток;
• записать число противоположное полученному.

Пример

Разделить 17 на −5 с остатком.

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.

Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.

Ответ: 17 : (− 5) = −3 (остаток 2).

Деление с остатком целого отрицательного числа на целое положительное

Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:

Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:

d = a − b * c

Из правила делаем вывод, что при делении получается целое неотрицательное число.

Для точности решения применим алгоритм деления а на b с остатком:

• найти модули делимого и делителя;
• разделить по модулю;
• записать противоположное данному число и вычесть 1;
• использовать формулу для остатка d = a − b * c.

Рассмотрим пример, где можно применить алгоритм.

Пример

Найти неполное частное и остаток от деления −17 на 5.

Разделим заданные числа по модулю.

Получаем, что при делении частное равно 3, а остаток 2.

Так как получили 3, противоположное ему −3.

Необходимо отнять единицу: −3 − 1 = −4.

Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:

d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.

Значит, неполным частным от деления является число −4 с остатком 3.

Ответ: (−17) : 5 = −4 (остаток 3).

Деление с остатком целых отрицательных чисел

Сформулируем правило деления с остатком целых отрицательных чисел:

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:

d = a − b * c

Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.

Алгоритм деления с остатком целых отрицательных чисел:

• найти модули делимого и делителя;
• разделить модуль делимого на модуль делителя;
• получить неполное частное и остаток;
• прибавить 1 к неполному частному;
• вычислить остаток, исходя из формулы d = a − b * c.

Пример

Найти неполное частное и остаток при делении −17 на −5.

Применим алгоритм для деления с остатком.

Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.

Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.

Получилось, что остаток равен 3, а неполное частное равно 4.

Ответ: (−17) : (−5) = 4 (остаток 3).

Деление с остатком с помощью числового луча

Деление с остатком можно выполнить и на числовом луче.

Пример 1

Рассмотрим выражение: 10 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.

Решение: 10 : 3 = 3 (остаток 1).

Пример 2

Рассмотрим выражение: 11 : 3.

Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.

Решение: 11 : 3 = 3 (остаток 2).

Проверка деления с остатком

Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.

Формула деления с остатком

a = b * c + d,

где a — делимое, b — делитель, c — неполное частное, d — остаток.

Эту формулу можно использовать для проверки деления с остатком.

Пример

Рассмотрим выражение: 15 : 2 = 7 (остаток 1).

В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.

Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:

Теорема о делимости целых чисел с остатком

Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:

где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.

Докажем возможность существования a = b * q + r .

Доказательство:

Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.

Если посчитать, что b — целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b * q не было больше значения числа а , а произведение b * (q + 1) было больше, чем a.

Тогда необходимо взять q такое, чтобы данное неравенством b * q

Источник

Изучение темы » Деление с остатком»

Тема: Изучение деления с остатком в начальной школе.

В основе разъяснения смысла деления с остатком лежит теоретико-множественная трактовка определения: «Разделить с остатком целое неотрица­тельное число a на натуральное число b — значит найти целые неотрица­тельные числа q и r , что a = bq + r и 0 r b ».

Деление с остатком вво­дится после внетабличного умножения и деления и является подготовкой к письменному делению многозначных чисел.

Для того чтобы учащиеся хорошо усвоили новый материал, им необходимо знать из ранее пройденного такие вопросы: 1) смысл деления; 2) табличные случаи деления без остатка.

ЭТАПЫ ИЗУЧЕНИЯ темы «Деление с остатком»:

Цель- ознакомить с конкретным смыслом деления с остатком, опираясь на предметные действия.

На этом этапе решаются практические задачи на деление с остатком, вво­дится форма записи деления с остатком. Все задачи решаются практически.

На этом уроке уч-ся убеждаются в том, что большее число всегда можно разделить на меньшее, только иногда при делении получается остаток.

При подборе практических заданий для разъяснения смысла деления с ос­татком лучше использовать ситуации, связанные с делением по содержанию, так как процесс этого деления можно показать не только на предметных мно­жествах, но и иллюстрировать.

Первую задачу целесообразно подобрать так, чтобы она носила проблем­ный характер. Причем решение задачи желательно сопровождать практической демонстрацией.

Рассмотрим конкретные примеры:

В результате практической работы с демонстрационным материалом дети убеждаются в том, что иногда при делении могут остаться предметы

— Для ответа на вопрос задачи 1 надо узнать, сколько раз по 5 содержится в 14.

— В 14 содержится 2 раза по 5 и еще остается 4.

Выполненные действия переводятся на язык математических знаков:

— Сколько было мячей? (14) Запишем это.

— Что мы делали с мячами? (Раздавали игрокам по 5 штук в каждому).

Читайте также:  Правильный способ написания букв

— Скольким игрокам смогли раздать? (2) Сколько мячей осталось? (4). Решение записы­вают так:

При знакомстве с формой записи деления с остатком важно обратить внимание на то, что обозначает каждое число в этой записи.

При знакомстве с делением с остатком вводится новый вид записи действия деления – «уголок»

Цель — на основе наблюдений подвести детей к выводу: остаток при делении всегда меньше делителя.

В качестве подготовки можно использовать следующие упражнения:

1) Повторить ряды чисел из таблицы умножения, делящиеся на данное число («Назовите числа, которые делятся на 2 без остатка»).

2) Можно провести игру: учитель называет подряд числа от 1 до 30. Уч-ся вни­мательно слушают его и, когда он называет число, делящееся без остатка, на­пример на 3, поднимают руку или хлопают в ладоши.

Для раскрытия соотношения между делителем и остатком в учебниках предлагаются следующие задания:

Одновременно учитель заполняет таблицу:

Ученики замечают, что при делении на 2 в остатке получается 0 или 1; при делении на 3 остатки могут быть равны 0, 1 или 2.

На основании знания таблицы деления ученики выполняют деление не­скольких последовательных чисел на 4, 5 и продолжают заполнение таблицы:

— Сравните делитель и остатки и сделайте вывод.

Упражнения для закрепления:

Цель — познакомить с приемом подбора, делимого для нахождения частного и остатка.

1) Назови все числа, которые без остатка делятся на 2, на 3 и т.д.

2) Среди данных чисел выбери числа, которые без остатка делятся на 5, на 7 и т.д.

3) Назови число, ближайшее к числу 60, которое меньше, чем 60, и делится на 9 без остатка.

4) Среди данных чисел 45, 46, 47 выбери ближайшее к числу 48 число, которое меньше, чем 48 и делится на 5 без остатка.

На этом этапе вводится знакомство с алгоритмом проверки деления с остатком:

Цель — познакомить учащихся с приемом подбора частного при делении с ос­татком.

Прием, с которым знакомятся ученики (подбор такого числа, при умно­жении которого на делитель получается число, близкое к делимому), более тру­доемкий, чем прием подбора делимого. Однако многократное умножение част­ного на делитель способствует запоминанию таблицы умножения.

Цель — познакомить учащихся со случаем деления с остатком меньшего числа на большее.

С этой целью предлагаются задачи:

Решая задачи, учащиеся приходят к выводу, что при делении меньшего числа на большее частное равно 0, а остаток равен делимому.

В некоторых учебниках этот этап даётся учащимся с опорой на прием подбора де­лимого:

Цель — познакомить учащихся со способом проверки деления с остатком.

В качестве подготовки надо вспомнить правило проверки деления умно­жением. Анализируя образец в учебнике, ученики высказывают свои предположения о проверке деления с остатком.

Выясняется, что для проверки деления с остатком надо сравнить остаток с делителем: если остаток больше делителя, то деление выполнено неправиль­но; если остаток меньше делителя, то частное надо умножить на делитель и прибавить остаток. Если полученное число равно делимому, то вычисления вы­полнены правильно.

Деление с остатком – случай, который при решении практических задач встречается гораздо чаще, чем деление без остатка. Поэтому знакомство с ним имеет большое практическое значение хотя бы в этом смысле. Это важно ещё и потому, что в школьной практике дети, постоянно встречаясь только со случаями деления без остатка (в течение всей работы над темой «Умножение и деление в пределах 100»), часто приходят к убеждению, что, например, 8 разделить на 3 вообще нельзя. Если на практике им приходится сталкиваться с такой задачей, то они теряются и не знают, что делать. Поэтому нужно сделать всё для того чтобы такие задачи не «пугали» детей, и чтобы они в дальнейшем не объясняли «опечаткой» в условии задания такие случаи деления.

Деление с остатком нужно хорошо знать для сознательного усвоения алгоритмов письменных вычислений. Это ещё одна из причин, из-за которой этому вопросу следует уделить повышенное внимание.

Навык деления с остатком вырабатывается в результате тренировки, по­этому надо больше включать примеров на деление с остатком как в устные уп­ражнения, так и в письменные работы, при этом обращать внимание, что част­ное находят делением, а остаток — вычитанием.

Источник