Способы проекции прямой линии

Проекции прямых линий

Положение прямой линии в пространстве вполне определяется двумя ее любыми точками. В общем случае проекцией прямой является прямая, в частном случае — точка, если прямая перпендикулярна плоскости проекций. Для построения проекций прямой достаточно иметь либо проекции двух ее точек, либо проекцию одной точки прямой и направление прямой в пространстве.

По своему расположению в пространстве относительно плоскостей проекций прямые линии разделяют на прямые общего положения, уровня и проецирующие.

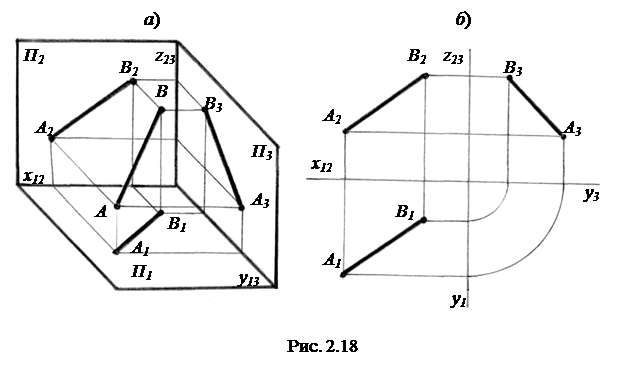
2.2.1. Прямые общего положения.Это прямые, не параллельные и не перпендикулярные к плоскостям проекций. Проекции А₁В₁, А₂В₂ и А₃В₃ отрезка АВ прямой АВ общего положения (рис. 2.18, а) наклонены под острыми углами к осям x₁₂, y₁₃ и z₂₃. Длины проекций отрезков этой прямой всегда меньше самого отрезка. Трехкартинный комплексный чертеж отрезка прямой общего положения, построенный по двум точкам А и В, показан на рис.2.18, б.

2.2.2. Прямые уровня. Это прямые, параллельные одной из плоскостей проекций — П₁, П₂ или П₃. Следовательно, имеем три вида прямых уровня:

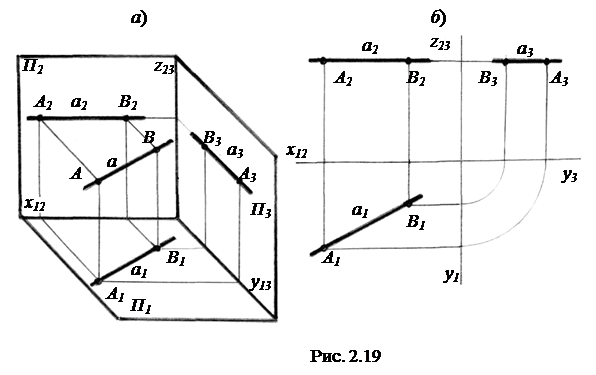
1) горизонтальная уровня a (горизонталь), параллельная П₁ (прямая a с отрезком AB на ней на рис. 2.19, а, б);

2) фронтальная уровня (фронталь), параллельная П₂ (прямая b c отрезком CD на ней на рис. 2.20, а);

3) профильная уровня, параллельная П₃ (прямая с с отрезком ЕF на ней на рис. 2.20, б). На рис. 2.20 наглядные изображения прямых b и c относительно плоскостей проекций не показаны.

Одноименные проекции отрезков прямых уровня проецируются в натуральную величину, а разноименные параллельны осям, отделяющим их от одноименных. При этом для горизонтали одноименная проекция — горизонтальная, а разноименные — фронтальная и профильная и т. п.

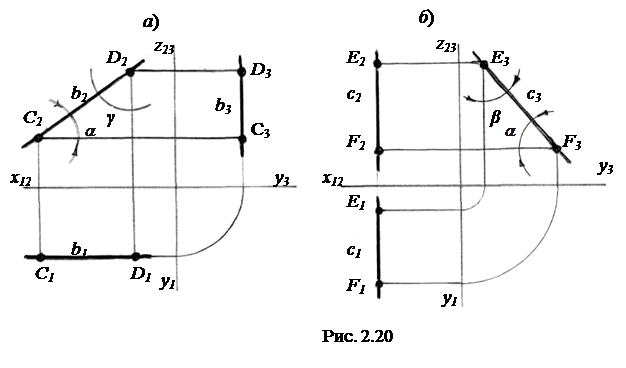
Углы наклона прямых уровня a, b и c к плоскостям проекций П₁, П₂ и П₃ принято обозначать соответственно α, β и γ (на рис. 2.19 углы α, β и γ не показаны).

2.2.3. Проецирующие прямые.Это прямые, перпендикулярные к одной из плоскостей проекций и параллельные двум другим. Следовательно, имеем три вида проецирующих прямых:

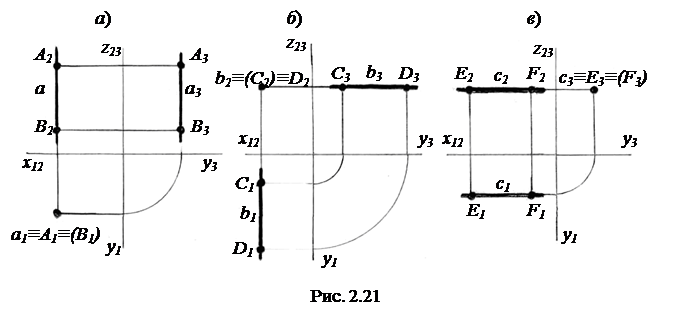
1) горизонтально-проецирующая прямая, перпендикулярная П₁ (прямая а с отрезком AB на ней на рис. 2.21, а);

2) фронтально-проецирующая прямая, перпендикулярная П₂ (прямая b с отрезком CD на ней на рис. 2.21, б);

3) профильно-проецирующая прямая, перпендикулярная П₃ (прямая c с отрезком EF на ней на рис. 2.21, в).

На рис. 2.21 в скобки заключены проекции невидимых точек. Вопрос определения видимости точек на проекциях подробнее будет рассмотрен ниже в п. «Скрещивающиеся прямые».

У проецирующих прямых одноименные проекции представляют собой точки, что вытекает из существа проецирующей прямой, вдоль которой ведется проецирование.

Каждая разноименная проекция проецирующей прямой перпендикулярна оси, отделяющей ее от одноименной проекции, а разноимённая проекция отрезка, расположенного на прямой уровня, является натуральной величиной этого отрезка.

2.2.4. Определение натуральной величины отрезка прямой общего положения.Натуральную величину прямой частного положения можно сразу определить на комплексном чертеже этой прямой.

Для определения натуральной величины отрезка прямой общего положения можно применить рассмотренный ранее (см. п. 2.1.2) способ замены плоскостей проекций. На рис.2.22 показано определение натуральной величины (Н.В.) отрезка AB прямой общего положения и определение углов наклона его к Π₁ ( угол α) и к Π₂ ( угол β) этим способом.

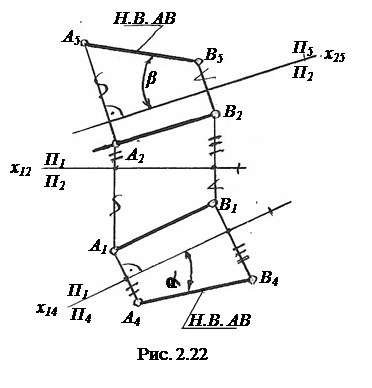
Дополнительная плоскость Π₄проведена параллельноAB (х₁₄||A₁B₁). Прямая AB преобразована в положение фронтали, следовательно A₄B₄ – натуральная величина AB.

Проведя дополнительную плоскостьΠ₅||AB (х₂₅||A₂B₂), также можно определить натуральную величинуAB. A₅B₅ – натуральная величинаAB. Прямая AB в системе Π₂—Π₅ стала горизонталью.

На рис.2.23 показано определение натуральной величины ABметодом треугольника.Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – алгебраическая разность расстояний его концов от плоскости Π₁ (ΔZ).

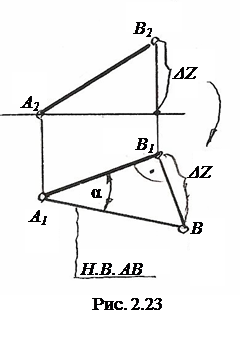
2.2.5. Взаимное положение прямых.Прямые линии в пространстве могут быть параллельными, пересекаться и скрещиваться.

Параллельные прямые. Из свойств параллельных проекций следует, что если прямые в пространстве параллельны, то все три пары их одноименных проекций параллельны. Очевидно и обратное положение: если одноименные проекции прямых параллельны, то прямые в пространстве параллельны.

Для определения параллельности прямых в общем случае достаточно параллельности двух пар одноименных проекций. В случае, если определяется параллельность линий уровня, то одной из двух пар параллельных проекций должна быть проекция на одноименную плоскость.

На рис. 2.24 показаны проекции параллельных прямых a и b общего положения, где a₁║ b₁ и a₂║ b₂. На рис. 2.25 показаны две горизонтали c и d. У горизонталей фронтальные и профильные проекции всегда параллельны осям, отделяющих их от одноименных горизонтальных проекций, т. е. c₂║ d₂║ x₁₂ и c₃║ d₃║ y₃. Но горизонтальные их проекции не параллельны, т. е. c₁╫ d₁. Следовательно, прямые c и d не параллельны.

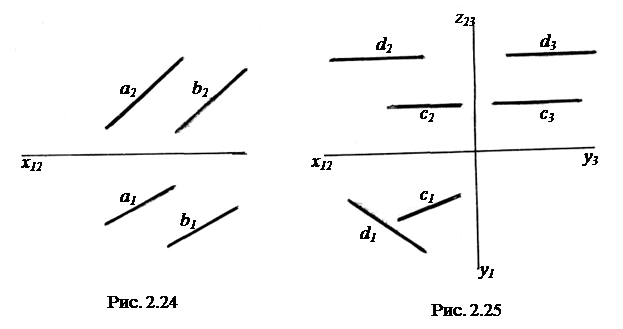
Пересекающиеся прямые. Две пересекающиеся прямые лежат в одной плоскости и имеют одну общую точку. Из свойств параллельных проекций известно, что если точка лежит на прямой, то ее проекции лежат на проекциях прямой. Если точка лежит и на той и на другой прямой, т. е. в точке пересечения прямых, то ее проекция должна лежать сразу на двух одноименных проекциях прямых, а следовательно, в точке пересечения проекций прямых.

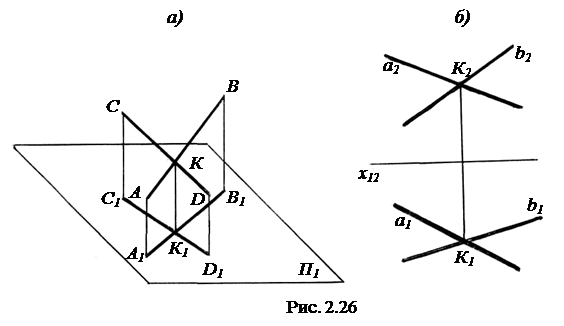
Так, если отрезки AB и CD двух прямых пересекаются в точке K, то проекции отрезков A₁B₁ и C₁D₁ пересекаются в точке K₁, являющейся проекцией точки K (рис. 2.26, а). Поэтому, если одноименные проекции прямых пересекаются в точках, лежащих на одной линии проекционной связи, то прямые в пространстве пересекаются (рис. 2.26, б).

Для определения того, пересекаются прямые или нет, достаточно, чтобы это условие выполнялось для двух каких-либо проекций. Исключение составляет случай, когда одна из пересекающихся прямых является профильной уровня. В этом случае для проверки пересечения прямых необходимо построение профильной проекции.

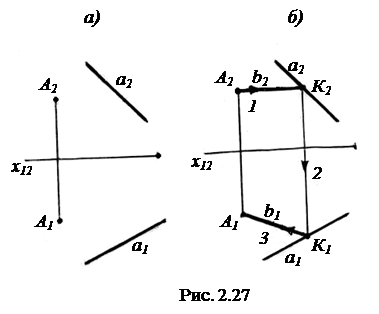
Пусть через точку A необходимо провести горизонталь b, пересекающую прямую a (рис. 2.27, а). Для этого через точку A₂ проводим b₂║ x₁₂ (этап 1) до пересечения с a₂ в точке K₂ (рис.2.27, б). Далее с помощью линии проекционной связи на a₁ находим точку K₁ (этап 2) и, соединяя точки A₁ и K₁ (этап 3), получаем b₁.

Скрещивающиеся прямые.Скрещивающиеся прямые a и b не лежат в одной плоскости и, следовательно, не параллельны и не имеют общих точек (рис.2.28, а). Поэтому, если прямые скрещивающиеся, то хотя бы одна пара их одноименных проекций не параллельна, и точки пересечения одноименных проекций не лежат на одной линии проекционной связи (рис. 2.28, б).

Каждая такая точка пересечения является проекцией двух точек, принадлежащих прямым; эти две точки лежат на одном проецирующем луче и называются конкурирующими.

K1≡(L1)

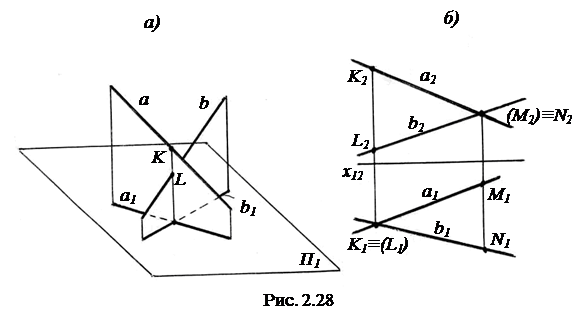
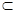
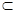
Точки K и L (рис. 2.28, а) лежат на одном горизонтально-проецирующем луче. Горизонтальные проекции точек совпадают и находятся в точке пересечения горизонтальных проекций a₁ и b₁ прямых. Точка K a, точка L b. Видно, что точка K выше точки L. Считают, что при проецировании на П₁ точка K видна, а точка L — не видна (закрыта от наблюдателя точкой К).

Точки M и N лежат на одном фронтально-проецирующем луче (рис. 2.28, б). Фронтальные проекции точек совпадают и находятся в точке пересечения фронтальных проекций прямых a₂ и b₂. Точка M 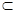a, точка N b. Точка N дальше от П₂, чем точка M, т. е. ближе к глазам наблюдателя, и поэтому при проецировании на П₂ точка N видна, а точка M — не видна. Обозначения проекций невидимых точек принято заключать в круглые скобки.

Источник

Проецирование отрезка прямой линии с примерами и образцами выполнения

Содержание:

Проецирование отрезка прямой на горизонтальную, фронтальную и профильную плоскости проекции заключает-ся в построении соответствующих проекций двух точек, при-надлежащих данной прямой, и проведении прямой линии че-рез одноименные проекции этих точек.

Проецирование отрезка прямой линии

Отрезок прямой линии определяется двумя точками, которые находятся на концах этого отрезка.

Проецирование отрезка прямой линии на плоскости проекций

Прямая линия АВ определяется двумя точками, которые находятся на концах отрезка.

Прямоугольную проекцию отрезка АВ можно построить следующим образом (рис. 89, а).

Опустив перпендикуляры из точек А и В на плоскость Н. получим проекции а и b этих точек. Соединив точки а и b прямой линией, получим искомую горизонтальную проекцию отрезка АВ.

Если взять на отрезке прямой линии АВ точки А, С, D, Е, В (рис. 89. б) и из каждой точки опус­тить перпендикуляры на плоскость Н. то совокупность этих перпендикуляров можно рассматривать как плоскость Q, перпендикулярную плоскости Н. Плоскость Q пересечет плоскость Н по прямой линии, на которой располагаются точки пересече­ния всех перпендикуляров с плоскостью Н. Так как эти точки являются проекциями точек отрезка АВ. то, следовательно, и отрезок ab будет проекцией отрезка АВ. Таким образом, проек­цию отрезка АВ на плоскости Н можно по­лучить, если через отрезок АВ провести плос­кость Q, перпендикулярную плоскости Н, до их взаимного пересечения. Линия пересечения плоскостей и будет горизонтальной проекцией отрезка АВ.

На рис. 89. в показано построение фронталь­ной проекции отрезка АВ. Плоскость Р перпенди­кулярна плоскости V.

Рассмотрим различные случаи расположения отрезков прямой линии относительно плоскостей проекций Н. V и W.

1. Прямая, перпендикулярная плоскости V, называется фронтально-проецирующей прямой (рис. 90, о).

Из комплексного чертежа отрезка АВ (рис. 90, б) видно, что горизонтальная проекция ab перпендикулярна оси х и по длине равна отрез­ку АВ, а фронтальная проекция а’Ь’ является точкой.

Если, например, резец расположить так, чтобы его длинные ребра были параллельны плоскостям V и Н, то ребро АВ будет фронтально проецирую­щей прямой (рис. 90, в).

2. Прямая, перпендикулярная плоскости Н (рис. 91. а), называется горизонтально-проециру­ющей прямой.

Из комплексного чертежа отрезка ВС (рис. 91, б) видно, что фронтальная проекция b‘с’ перпендикулярна оси х и по длине равна отрезку ВС, а горизонтальная проекция bс (точки совпадают) является точкой.

Ребро ВС резца на рис. 91, в является горизон­тально- проецирующей прямой.

3. Прямая, перпендикулярная плоскости W, называется профильно-проецирующей прямой (рис. 92, а). На комплексном чертеже обе проек­ции отрезка АВ — фронтальная и горизонтальная — параллельны оси Ох и по длине равны отрезку АВ (рис. 92, 6). Профильная проекция а«Ь» отрез­ка АВ — точка.

Длинное ребро АВ резца (рис. 92. в) — профильно-проецирующая прямая.

4. Прямая, параллельная горизонтальной пло­скости проекций, называется горизонтальной прямой или горизонталью (рис. 93. а). На комплексном чертеже горизонтали АВ (рис. 93, б) видно, что фронтальная а’Ь’ и профильная а»Ь» проекции параллельны соответственно осям про­екций Ох и Oy₁. Горизонтальная проекция ab горизонтали АВ расположена под углом к оси Ох и равна длине отрезка АВ.

Ребро АВ (режущая кромка) головки резца (рис. 93, в) параллельно плоскости Н и представ­ляет собой горизонталь.

5. Прямая, параллельная плоскости У, называ­ется фронтальной прямой или фронталью (рис. 94, а).

Горизонтальная проекция ab фронтали АВ параллельна оси Ох (рис. 94, б). Фронталь­ная проекция а‘Ь‘ фронтали наклонена к оси Ох и равна действительной длине отрезка АВ. Профильная проекция а»Ь» фронтали АВ па­раллельна оси Oz.

Ребро АВ резца (рис. 94, в) параллельно плос­кости V и, следовательно, представляет собой фронталь.

6. Прямая, не параллельная ни одной из трех плоскостей проекций, называется прямой общего положения.

Возьмем отрезок АВ прямой общего положения (рис. 95, а) и построим горизонтальную ab и фронтальную а’Ь’ проекции этого отрезка. Ком­плексный чертеж отрезка прямой общего положе­ния показан на рис. 95, б.

По двум проекциям а’Ь’ и ab отрезка прямой общего положения можно, применяя известное уже правило (см. рис. 86, б), построить третью проекцию а»Ь» (рис. 95. б).

У отрезного резца (рис. 95. а) ребро АВ пред­ставляет собой прямую общего положения.

Рассмотренные прямые часто применяются в построениях, поэтому, изучая их комплексные чертежи. надо запомнить. как та или иная проек­ция прямой располагается относительно осей про­екций.

Угол между прямой и плоскостью проекций

Горизонталь, фронталь, профильная прямая и прямая общего положения расположены под углом к соответствующим плоскостям проекций.

Угол прямой линии с плоскостью проекций определяется как острый угол между этой прямой и ее проекцией на данную плоскость. Например, отрезок фронтали АВ (рис. 96, а) составляет угол α с горизонтальной плос­костью проекций Н.

Разберем способ определения угла между пря­мой и плоскостью проекций на комплексном чер­теже. Если прямая — фронталь, то, как видно на рис. 96, б, угол между фронтальной и горизонталь­ной плоскостью проекций Н на комплексном чер­теже равен углу между фронтальной проекцией фронтали а’b’ и осью проекций х.

Ребро АВ резьбового резца (рис. 96, в) парал­лельно фронтальной плоскости проекций, т.е. ребро АВ — фронталь. Так как основание резца расположено на горизонтальной плоскости проек­ций Н, то угол α является углем между прямой АВ и плоскостью Н. Таким образом, по чертежу резца можно определить угол α между ребром АВ и основанием резца. Следовательно, сети прямая имеет какую-либо проекцию, равную действи­тельной се длине, то на комплексном чертеже угол между проекцией этой прямой и плоскостью проекций будет действительным углом.

Следы прямой линии

Следом прямой линии называется точка пере­сечения прямой с плоскостью проекций.

Чтобы найти фронтальный след прямой АВ (рис. 97, а), необходимо продолжить се горизонтальную проекцию ab до пересечения с осью х в точке v, а затем из точки v восставить перпенди­куляр к оси х и найти точку v‘ пересечения этого перпендикуляра с продолжением фронтальной проекции отрезка. Тогда v’ — искомый фронталь­ный след прямой АВ или точнее — фронтальная проекция фронтального следа; точка v — горизонтальная проекция горизонтального следа; точка h’ фронтальная проекция горизонтального следа.

На комплексном чертеже отрезка АВ эти по­строения выполняются аналогично (рис. 97, б).

Из чертежа видно, что одна из двух проекций каждого следа прямей расположена на оси х.

Изображение взаимного положения двух прямых на комплексном чертеже

Из курса начертательной геометрии известно, что:

а) если прямые параллельны в пространстве, то их одноименные проекции параллельны (рис. 98, д);

б) если прямые пересекаются в точке А. то их одноименные проекции тоже пересекаются (рис. 98, б); при этом проекции точки пересечения А обязательно располагаются на самом пер­пендикуляре к оси (на одной линии связи);

в) если точки пересечения проекций прямых, например, n’ и а не расположены на одном пер­пендикуляре к оси х (рис. 98, в). то прямые скре­щиваются.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник