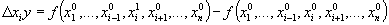Способы применяемые для кратных моделей

Экономический анализ. Шпаргалки.

90. Мультипликативная модель, смешанные и кратные модели, логарифмический способ и способ долевого участия.

Мультипликативная модель представляет собой произведение факторов:

Примером мультипликативной модели является двухфакторная модель объема реализации.

Где Ч – среднесписочная численность работников; В – выработка на одного работника.

Кратные модели представляют собой отношение факторов и имеют вид.

Где Z – совокупный показатель.

Смешанные модели представляют собой комбинацию перечисленных моделей. Примером смешанной модели является формула расчета интегрального показателя рентабельности:

Где R к – рентабельность капитала; Rnр – рентабельность продаж; F е —фондоемкость основных средств; Е з – коэффициент закрепления оборотных средств. Логарифмический способ применим к кратным и мультипликативным моделям. Основан на логарифмировании отклонения отчетного и базисного значений результативного признака, равного отношению соответствующих произведений факторов, так как изменение показателей может быть оценено с помощью как абсолютных, так и относительных показателей. Способ долевого участия заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост совокупного показателя. Он применяется к аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков. Для примера можно рассмотреть модель зависимости фонда заработной платы от средней заработной платы и численности персонала: ФЗ = ЗП · Ч, где ФЗ – фонд заработной платы; ЗП – средняя заработная плата; Ч – среднесписочная численность.

Источник

Кратные модели

Применяются, когда результативный показатель получают делением одного факторного показателя на величину другого.

Смешанные (комбинированные) модели – сочетание предыдущих моделей в различных комбинациях.

Способ цепной подстановки.

Заключ-ся в определении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на отчетные.

Данный способ основан на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом исходя из того, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения. потом изменяются два при неизменности остальных и т.д.

ВП=КР*ГВ Алгоритм расчета способом ЦП: ВППЛ=КРПЛ*ГВПЛ; ВПУСЛ= КРФ*ГВПЛ ;

ВПФ=КРФ*ГВФ

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.

Это связано с тем, что в результате применения этого метода образуется

некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки: при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов; если модель представлена несколькими количественными и качественными показателями, последовательность подстановки определяется путем логического анализа.

Способ абсолютных разниц.

Способ абсолютных разниц: является модификацией способа цепной подстановки.

Изменение результативного показателя за счет каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки.

Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных и смешанных моделях вида у = (а – в) . с. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах. Чтобы рассчитать влияние второго фактора нужно к плановой величине результативного показателя прибавить изменения за счет 1-го фактора, затем полученную сумму умножить на относительный прирост второго фактора (дней в %) и разделить на 100%.

Источник

Вопрос № 18. Способы преобразования кратных факторных моделей.

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.

Удлинение предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет разложения одного или нескольких факторных показателей на составные элементы

Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей.

Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель

На практике для преобразования одной и той же модели может быть последовательно использовано несколько методов.

Вопрос № 19. Методы детерминированного факторного анализа: изолированного влияния факторов, цепных подстановок.

Изменение результативного показателя под влиянием какого-либо фактора вычисляется по формуле:

При использовании данного метода полное разложение не достигается, т. е. сумма влияний всех факторов не равна общему приросту результативного показателя. Этот метод позволяет только приблизительно оценить степень влияния факторов, но, с другой стороны, он является самым простым методом и не требует установления очередности изменения факторов.

Метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных значений факторов на отчетные. Данный способ основан на элиминировании. Элиминировать — значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Предполагается, что все факторы изменяются независимо друг от друга, т.е. сначала изменяется один фактор, а все остальные остаются без изменения, потом изменяются два при неизменности остальных и т.д.

Преимущества данного способа: универсальность применения; простота расчетов.

Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют определенные правила, определяющие последовательность подстановки:

— при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;

— если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.

Вопрос № 20. Методы детерминированного факторного анализа: относительных и абсолютных разниц.

Метод абсолютных разниц является модификацией способа цепной подстановки. Изменение результативного показателя за счет каждого фактора определяется как произведение абсолютного прироста исследуемого фактора на базисную величину факторов, которые находятся справа от него и отчетную величину факторов, расположенных слева от него в модели.

Метод относительных разниц также является одной из модификаций способа цепной подстановки. Применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных моделях. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах — находят относительное отклонение каждого факторного показателя; определяют отклонение результативного показателя у за счет каждого фактора

Источник

Большая Энциклопедия Нефти и Газа

Кратная модель

Кратные модели могут быть преобразованы путем удлинения, расширения и сокращения. [1]

Метод расширения кратной модели представляет собой получение мультипликативной системы путем умножения числителя и знаменателя дроби исходной факторной модели на один или несколько новых показателей. [2]

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. [3]

К классу кратных моделей применяют следующие способы их преобразования: удлинения, расширения и сокращения. [4]

Метод расширения кратной модели представляет собой получение мультипликативной системы путем умножения числителя и знаменателя дроби исходной факторной модели на один или несколько новых показателей. [5]

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. [6]

Удлинение знаменателя в кратных моделях позволяет получить также кратную модель, где фактор, обратно пропорционально влияющий на результативный показатель, будет представлен суммой или произведением однородных показателей. [7]

Задача имеет смысл для мультипликативных и кратных моделей . [8]

Задача имеет смысл для мультипликативных и кратных моделей . [9]

Исходная кратная модель заменяется на тождественную кратную модель , в которой каждый фактор — отдельная кратная модель. [10]

Метод арифметических разниц нецелесообразно использовать для кратных моделей . [11]

В факторном анализе индексный метод используется в мультипликативных и кратных моделях . [12]

Удлинение знаменателя в кратных моделях позволяет получить также кратную модель , где фактор, обратно пропорционально влияющий на результативный показатель, будет представлен суммой или произведением однородных показателей. [13]

Исходная кратная модель заменяется на мультипликативную модель, в которой каждый фактор — отдельная кратная модель . [14]

Исходная кратная модель заменяется на тождественную кратную модель, в которой каждый фактор — отдельная кратная модель . [15]

Источник

Может быть использована специалистами предприятий. Книга выпущена в свет в рамках межиздательского проекта «Учебник для XXI века»

Главная > Учебник

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

5.4. Детерминированное моделирование и преобразование факторных систем

Сущность и значение моделирования, требования к нему. Основные типы факторных детерминированных моделей. Способы преобразования факторных моделей. Правила моделирования.

Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.

Моделирование — это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения.

В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).

При моделировании детерминированных факторных систем необходимо выполнять ряд требований.

1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.

2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции. Последнее можно проиллюстрировать следующим образом. Возьмем две модели:

2)ГВ=ВП/ЧР, где ВП — валовая продукция предприятия; ЧР — численность работников на предприятии; ГВ — среднегодовая выработка продукции одним работником.

В первой системе факторы находятся в причинной связи с результативным показателем, а во второй — в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая.

3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность.

4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.

1. Аддитивные модели:

Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

2. Мультипликативные модели:

Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.

3. Кратные модели:

Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.

4. Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей:

Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции (см. рис. 5.2) можно применять такие детерминированные модели, как:

Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы.

Как известно, объем реализации продукции равен:

V РП = VB П — V И,

где VB П — объем производства; V И — объем внутрихозяйственного использования продукции.

В хозяйстве продукция использовалась в качестве семян (С) и кормов (К). Тогда приведенную исходную модель можно записать следующим образом: V РП = VB П — (С + К).

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения.

Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции ( VB П). Исходная модель этой факторной системы будет иметь вид

Если общую сумму затрат (3) заменить отдельными их элементами, такими, как заработная плата (3П), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы ( HP ) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:

где Х 1 — трудоемкость продукции; Х 2 — материалоемкость продукции; Х 3 — фондоемкость продукции; Х 4 — уровень накладных расходов.

Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Если В = L +М+N+Р,то

В результате, получили конечную модель того же вида, что и исходной факторной системы (кратную модель). На практике такое разложение встречается довольно часто. Например, при анализе показателя рентабельности производства ( R ):

где П — сумма прибыли от реализации продукции; 3 — сумма затрат на производство и реализацию продукции. Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид:

Себестоимость одного тонно-километра зависит от суммы затрат на содержание и эксплуатацию автомобиля (3) и от его среднегодовой выработки (ГВ). Исходная модель этой системы будет иметь вид: С ткм = 3 / ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д), продолжительности смены (П) и среднечасовой выработки (ЧВ), мы можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов:

Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель

ввести новый показатель с, то модель примет вид

В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов.

Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП /ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками ( D ), то получим следующую модель годовой выработки:

где ДВ — среднедневная выработка; Д — количество отработанных дней одним работником.

После введения показателя количества отработанных часов всеми работниками (Г) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (Я):

Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель:

В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.

И снова практический пример. Как известно, экономическая рентабельность работы предприятия рассчитывается делением суммы прибыли ( П ) на среднегодовую стоимость основного и оборотного капитала предприятия ( KL ):

Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:

И еще один пример. Фондоотдача (ФО) определяется отношением валовой ( ВП ) или товарной продукции ( ТП ) к среднегодовой стоимости основных производственных фондов (ОПФ):

Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв):

Необходимо заметить, что на практике для преобразования одной и той же модели может быть последовательно использовано несколько методов. Например:

где ФО — фондоотдача; РП — объем реализованной продукции (выручка); С — себестоимость реализованной продукции; П — прибыль; ОПФ —среднегодовая стоимость основных производственных фондов; ОС — средние остатки оборотных средств.

В этом случае для преобразования исходной факторной модели, которая построена на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель, которая имеет большую познавательную ценность, так как учитывает причинно-следственные связи между показателями. Полученная конечная модель позволяет исследовать, как влияют на фондоотдачу рентабельность основных средств производства, соотношения между основными и оборотными средствами, а также коэффициент оборачиваемости оборотных средств.

Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.

Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.

Глава 6 СПОСОБЫ ИЗМЕРЕНИЯ ВЛИЯНИЯ ФАКТОРОВ В ДЕТЕРМИНИРОВАННОМ АНАЛИЗЕ

6.1. Способ цепной подстановки

Типы детерминированных моделей, в которых применяется способ цепной подстановки. Сущность и правила его применения. Алгоритмы расчета влияния факторов этим спосбом в различных типах моделей.

Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном факторном анализе (ДФА) для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.

Первых четыре способа основываются на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.

Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.

Порядок применения этого способа рассмотрим на следующем примере (табл. 6.1).

Как нам уже известно, объем валовой продукции ( ВП ) зависит от двух основных факторов первого уровня: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную мультипликативную модель: ВП = ЧР х ГВ.

Алгоритм расчета способом цепной подстановки для этой модели:

Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит за счет увеличения количества рабочих выпуск продукции увеличился на 32 000 млн руб. (192 000 — 160 000).

Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем валовой продукции увеличился на 48 000 млн руб. (240 000 — 192 000).

Таким образом, перевыполнение плана по объему валовой продукции явилось результатом влияния следующих факторов:

а) увеличения численности рабочих + 32 000 млн руб.

б) повышения уровня производительности труда + 48 000 млн руб.

Итого +80 000 млн руб.

Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:

Отсутствие такого равенства свидетельствует о допущенных ошибках в расчетах.

Для наглядности результаты анализа приведены в табл. 6.2.

Если требуется определить влияние трех факторов, то в этом случае рассчитывается не один, а два условных дополнительных показателя, т.е. количество условных показателей на единицу меньше числа факторов. Проиллюстрируем это на четырехфакторной модели валовой продукции:

Исходные данные для решения задачи приведены в табл.6.1:

План по выпуску продукции в целом перевыполнен на 80 000 млн руб. (240000 — 160000), в том числе за счет изменения:

а) количества рабочих

Используя способ цепной подстановки, рекомендуется придерживаться определенной последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки. Согласно схеме 5.2, количество рабочих в данном случае — фактор первого уровня подчинения, количество отработанных дней – второго уровня, продолжительность рабочего дня и среднечасовая выработка — факторы третьего уровня. Это и обусловило последовательность размещения факторов в модели и соответственно очередность их исследования.

Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.

Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.

В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:

где ФО — фондоотдача; ВП —валовая продукция; ОПФ — среднегодовая стоимость основных производственных фондов.

Методика расчета влияния факторов в смешанных моделях:

а) Мультипликативно-аддитивного типа П = VP П (Ц — С)

где П — сумма прибыли от реализации продукции; VP П — объем реализации продукции; Ц — цена реализации; С — себестоимость единицы продукции;

Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.

Отдельно необходимо остановиться на методике определения влияния структурного фактора на прирост результативного показателя с помощью этого способа. Например, выручка от реализации продукции (В) зависит не только от цены (Ц) и количества проданной продукции ( VPH ), но и от ее структуры (УД i ). Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:

В процессе анализа необходимо элиминироваться от воздействия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:

Разность между этими показателями учитывает изменение выручки от реализации продукции за счет изменения ее структуры (табл. 6.3.).

Из таблицы видно, что в связи с увеличением удельного веса продукции второго сорта в общем объеме его реализации выручка уменьшилась на 10 млн руб. (655 — 665). Это неиспользованный резерв предприятия.

6.2. Индексный метод

Сущность и назначение индексного метода. Алгоритм расчета влияния факторов этим методом для разных моделей.

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Для примера возьмем индекс стоимости товарной продукции:

Он отражает изменение физического объема товарной продукции ( q ) и цен (р) и равен произведению этих индексов:

Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен 1 p :

В нашем примере объем валовой продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки. Следовательно, индекс валовой продукции 1вп будет равен произведению индекса численности рабочих l чр и индекса среднегодовой выработки 1гв:

Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты валовой продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепной подстановки.

Источник