Способы применения эффекта холла

Применение эффекта Холла

С.А. МАНЕГО, Ю.А. БУМАЙ, В.В. ЧЕРНЫЙ

ЭФФЕКТ ХОЛЛА

Рекомендовано УМО по образованию в области приборостроения в качестве учебно-методического пособия для студентов специальностей

1-38 02 01Информационно-измерительная техника

1-38 02 03Техническое обеспечение безопасности

Минск

БНТУ

УДК 537,633,2 (075.8)

С.А. Манего, Ю.А. Бумай, В.В. Черный

Кафедра физики полупроводников и наноэлектроники БГУ,
С.Н. Собчук

М 23 Эффект Холла /сост. С.А. Манего, Ю.А. Бумай, В.В. Черный. ‒ Минск: БНТУ, 2014. 22 с.

Учебно-методическое пособие содержит в краткой форме теорию важнейшего из гальваномагнитных эффектов – эффекта Холла. Рассмотрены практические применения эффекта. Приведена также схема экспериментальной установки для исследования эффекта Холла. Показано, как на основании экспериментальных данных определяются важнейшие характеристики полупроводника – концентрация носителей заряда и их подвижность.

Учебно-методическое пособие предназначено для студентов инженерных специальностей, изучающих раздел “ Электричество и магнетизм ” курса общей физики.

УДК 537,633,2 (075.8)

ЭФФЕКТ ХОЛЛА

1. Изучить теоретические основы эффекта Холла.

2. Изучить связь параметров материалов с результатами измерений эффекта Холла.

1. Провести электрические измерения и измерения эффекта Холла.

2. Определить концентрацию и подвижность носителей тока в полупроводнике.

Гальваномагнитные эффекты

Физические явления, обусловленные движением носителей заряда под действием внешних и внутренних полей или разности температур, называются кинетическими явлениямиили явлениями переноса. К ним относятся электропроводность и теплопроводность, гальваномагнитные, термомагнитные и термоэлектрические явления. Кинетические явления лежат в основе фотоэлектрических и фотомагнитных эффектов. Среди многообразия кинетических эффектов под названием гальваномагнитных объединяются эффекты, возникающие в веществе, находящемся в магнитном поле, при прохождении через вещество электрического тока под действием электрического поля. Другими словами, гальваномагнитные явления наблюдаются в веществе при совместном действии электрического и магнитного полей. К важнейшим гальваномагнитным явлениямотносятся:

2. магниторезистивный эффект или магнетосопротивление;

3. эффект Эттингсгаузена, или поперечный гальваномагнитный эффект;

4. эффект Нернста, или продольный гальваномагнитный эффект.

Эффекты перечислены в порядке их практической значимости. Названия «продольный» и «поперечный» отражают направление градиентов температуры относительно тока. Рассмотрим эти эффекты

Эффект Холла

Американский физик Эдвин Герберт Холл в 1879 году впервые описал явление, впоследствии названное его именем. Явление, открытое Холлом, состоит в том, что в проводнике с током, помещенном в магнитное поле, перпендикулярное направлению тока, возникает электрическое поле в направлении, перпендикулярном направлениям тока и магнитного поля. Наиболее важным применением эффекта Холла является определение концентрации носителей зарядав материалах, проводящих электрический ток, в частности, в полупроводниках, у которых концентрацию носителей зарядов можно произвольно изменить, например, за счет введения примесей.

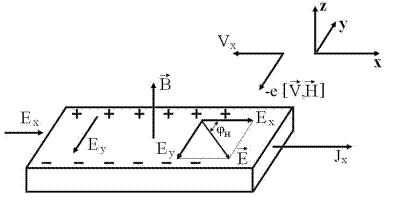
Обратимся к чисто примесному полупроводнику, для определенности электронному. Схема, иллюстрирующая возникновение эффекта Холла, изображена на рисунке 1.

К образцу прямоугольной формы, расположенному по длине вдоль оси Х, приложено электрическое поле Е, вызывающее электрический ток плотностью:

где: e – абсолютная величина заряда электрона; n – собственная концентрация электронов в объеме полупроводника.

Образец помещен в магнитное поле В, параллельно оси Z. В результате действия на движущиеся носители силы Лоренца

F= –e[V,B] (2)

электроны отклоняются в отрицательном направлении оси Y(дрейфовая скорость электронов Vнаправлена против тока) и скапливаются у боковой (передней) грани образца. Их накопление идет до тех пор, пока поперечное электрическое поле (поле Холла) не компенсирует поле силы Лоренца в направлении оси Y.

Вследствие появления поперечного поля Холла Ерезультирующее электрическое поле в образце конечных размеров будет повернуто относительно оси Х на некоторый угол φ_н (угол Холла), а ток будет идти лишь в направлении оси Х. Как видно из рисунка 1, угол определяется при этом соотношением:

(3),

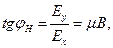
где μ – дрейфовая подвижность.

Поскольку поле Холла Е_y уравновешивает силу Лоренца, можно полагать, что оно должно быть пропорционально как приложенному полю В, так и току J_x в полупроводнике. Поэтому величину, называемую коэффициентом Холла, определяют так:

(4)

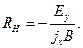
Следует обратить внимание на то, что, поскольку поле Холла направленно против оси Y (рис. 1), коэффициент R должен быть отрицательным.

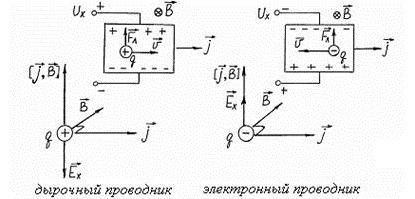
С другой стороны, если бы заряд носителей был положительным (в дырочном полупроводнике), знак их Х-компоненты скорости был бы обратным, и сила Лоренца осталась бы по направлению неизменной. В результате поле Холла, имело бы направление, противоположное тому, которое оно имеет при отрицательно заряженных носителях.

Из этого вывода следует, что по знаку ЭДС Холла можно определить знак носителей заряда и,следовательно, тип проводимости полупроводника.

Чтобы рассчитать коэффициент Холла, воспользуемся выражением для общей силы, действующей на электрон со стороны электрического и магнитного полей. В общем случае эта сила определяется векторным уравнением:

F= –еЕ– e[V,B]. (5)

Рис. 1. Схема возникновения эффекта Холла при действии силы Лоренца на движущиеся электроны.

Величина холловского поля определяется балансом сил в направлении оси Y, при котором F= 0. Отсюда:

Тогда, воспользовавшись соотношением (1), имеем:

. (7)

Сравнивая (4) и (7), видим, что:

(8)

Таким образом, коэффициент Холла обратно пропорционален концентрации носителейи ни от каких других параметров полупроводника не зависит. Знак «минус» показывает электронную проводимость, дырочной проводимости соответствует знак «плюс».

Для практического определения коэффициента Холла воспользуемся уравнением (7), заменив напряженность электрического поля E_y потенциалом поля.

(9)

В случае однородного образца мы имеем:

(10),

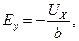
где U_x – холловская разность потенциалов или э.д.с.Холла. С учетом выражений (7) и (10) э.д.с. Холла равна:

, (11),

где: — a и b поперечные размеры образца, a, b(соответственно по направлениям z и y); I_x – сила тока, протекающая через образец; B_z – индукция магнитного поля.

В действительности произведенный элементарный вывод коэффициента Холла не точен: в нем предполагалось, что все носители имеют одинаковую дрейфовую скорость, и не учитывался характер распределения электронов по скоростям и механизм рассеяния носителей.

Более строгое выражение для коэффициента Холла имеет вид:

(12),

где r = 2 >/ 2 , r – называют холл-фактором, τ – время релаксации носителей заряда. Через n в данном случае обозначена концентрация носителей (электронов или дырок). Параметр r является атрибутом реального твердого тела и зависит от механизма рассеяния носителей.

Так, — при рассеянии на ионах примеси r = 315π/512 = 1,93, что обычно имеет место в области низких температур;

— при рассеянии на тепловых колебаниях решетки r = 3π/8 = 1,18 — соответствует более высокой области температур;

— при рассеянии на нейтральных примесях, а также в металлах и сильно вырожденных полупроводниках r = 1.

В полупроводнике со смешанной проводимостью в слабом магнитном поле ( ) коэффициент Холла равен

(13)

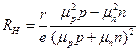
Так как в случае собственной проводимости n = p = n_i, то, введя b = μ_n / μ_p, для собственного полупроводника, получим:

, (14)

т. е. знак R_н определяется тем типом носителей тока, подвижность которых больше. Обычно отношение дрейфовых подвижностей b > 1 и R 3 /Кл. Тогда из формулы (12) можно найти концентрацию носителей заряда

(18)

(19)

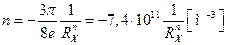
Одновременно с постоянной Холла определяют удельную проводимость образца «σ». Для образца с данными размерами (рис.2) удельная проводимость определяется по формуле:

(20)

(21)

(22)

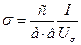
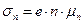
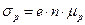
Отсюда, можно определить подвижность электронов и дырок:

(23)

(24)

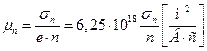
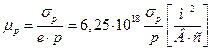
Применение эффекта Холла

На основе эффекта Холла можно создать ряд устройств и приборов, обладающих ценными и даже уникальными свойствами и занимающих важное место в измерительной технике, автоматике, радиотехнике и т. д. Приборы, созданные на основе эффекта Холла, называют датчиками Холла.

Датчики Холла позволяют измерять величину магнитного поля. Как видно из (11), при постоянной величине тока Э.Д.С. Холла прямо пропорциональна магнитной индукции. Линейная зависимость этих величин для датчиков Холла является преимуществом перед измерителями индукции на основе магнетосопротивления.

Датчики Холла также позволяют измерять электрические и магнитные характеристики металлов и полупроводников. В настоящее время в силу высокой точности, постоянства данных, надежности они нашли широкое применение в различных отраслях науки и техники. Датчики Холла могут применяться для измерения силы, давлений, углов, перемещений и других неэлектрических величин. При производстве полупроводниковых материалов эффект Холла используется для измерения подвижности и концентрации носителей в них. Для этой цели на специальном подготовленном образце измеряют э. д. с. Холла и по его величине судят о подвижности и концентрации носителей заряда материала, используемого для изготовления полупроводниковых приборов.

Датчики Холла используются в автомобилях, из-за их низкой стоимости, качества, надежности и способности противостоять жестким условиям окружающей среды. Датчики Холла используют в создании бесконтактных однополярных и биполярных выключателей и переключателей. Основные преимущества датчиков Холла — бесконтактность, отсутствие любых механических нагрузок и загрязнений.

Источник

Эффект холла — в чем заключается, применение для датчиков тока и положения, формула, квантовый, аномальный и другие виды

Электричество и магнитные поля существуют в тесной взаимосвязи друг с другом. Многие известные физики посвятили жизнь исследованию этой связи, поиску и описанию законов, на которых она базируется, а также способов применения на практике полученных теоретических сведений. Одним из таких учёных был Эдвин Герберт Холл, выдающийся американский исследователь, автор ценных научных материалов. В ходе одного из экспериментов он обнаружил необычное явление, которое со временем получило название «эффект Холла». Сегодня он массово используется в бытовой и компьютерной технике, электрооборудовании автомобилей, контрольно-измерительных приборах и, конечно, исследовательских лабораториях. Так в чём же физическая суть эффекта Холла и почему он не теряет своей актуальности спустя почти полтора века с момента открытия?

Что такое эффект Холла?

Эдвин Холл, пропуская ток через тонкую золотую пластину, расположенную между двумя магнитами, заметил, что носители заряда (электроны) отклоняются от центральной оси к одной из граней проводника. Таким образом, на этой грани возникает отрицательный заряд, а на противоположной — положительный. Возникшая разность потенциалов именуется холловским напряжением. Она строго перпендикулярна току в проводнике и вектору магнитной индукции. Это явление наблюдается не только в золоте, но и в любых проводниковых и полупроводниковых материалах, помещённых в магнитное поле.

Если проанализировать физическую суть, можно обнаружить, что у истоков накопления заряда на гранях проводника лежит сила Лоренца, с которой магнитное поле воздействует на заряженную частицу. Под её воздействием электроны будут накапливаться на грани проводника до тех пор, пока их суммарный заряд не скомпенсирует существующее магнитное поле.

В том же случае, когда внешнее магнитное поле слишком велико, система выйдет за рамки стабильности, и заряженные частицы начнут двигаться по циклоиде. Это называется несоблюдением критерия малости.

Цифровые датчики Холла делятся на униполярные и биполярные

Помимо эффекта Холла, законы которого описаны классической физикой и соблюдаются во всех нормальных или приближённых к нормальным условиям экспериментах, выделяют ещё несколько разновидностей явления возникновения разности потенциалов в проводнике.

Аномальный

Аномальным называют любой случай накопления заряда на грани проводника, в котором исключено воздействие внешних магнитных полей. Необходимым условием является перпендикулярная направленность разницы потенциалов относительно направления силы тока.

Причины, по которым возникает аномальный эффект Холла, обычно кроются в намагниченности металла-проводника или особенностях его молекулярной структуры.

Квантовый

Законы возникновения разницы потенциалов в «квантовом мире» исследуются на примере плоского проводника типа ДЭГ (двумерный электронный газ). Квантовый наблюдается в сильных магнитных полях и при низких температурах. Он выражается в квантовании холловского сопротивления, которое на графике имеет чётко выраженные «участки плато». Чем выше сопротивление, тем длиннее участки плато и выше разница между ними.

Открытие данного явления — одна из основных вех современной квантовой физики. Клаус фон Клитцинг, первооткрыватель квантового эффекта Холла, в 1985 году был удостоен Нобелевской премии.

Дробный

Многие передовые учёные в 80-х годах прошлого века заинтересовались исследованиями фон Клитцинга и продолжили изучать свойства разности потенциалов в ДЭГ. Наибольших успехов достигли Даниэль Цуи и Хорст Штёрмер, которые проанализировали промежуточные участки между «плато сопротивления» и пришли к выводу, что при существенном увеличении интенсивности магнитных полей «участки плато» можно получить и на дробных значениях электронных уровней Ландау, например, при n=1/3; n=2/5; n=3/7 и т. д.

Такое явление получило название дробного квантового эффекта Холла, а его первооткрыватели получили Нобелевскую премию по физике в 1998 году. В настоящее время ведутся расширенные исследования квантового и дробного квантового видов данного эффекта.

Спиновый

В 2003–2004 годах было изучено поведение электронов с антипараллельными спинами в проводниках, изолированных от каких-либо магнитных полей. Теоретической базой исследования послужили теории Владимира Переля, выдвинутые в далёком 1971 году. Они были доказаны на практике, когда удалось зафиксировать отклонения данных групп электронов к противоположным граням проводника. Движение заряженных частиц напоминает первый вид эффекта — аномальный.

Формулы и расчёты

Поскольку данный эффект базируется на силе Лоренца, то именно с её определения и начинается математическое описание возникшей разницы потенциалов. Сила Лоренца определяется из следующего выражения:

• q — заряд частицы;
• v — скорость движения частиц;
• B — внешнее магнитное поле.

Электрическое поле, сформированное образовавшимися на гранях проводника зарядами, тоже влияет на движущиеся в сечении электроны. Сила этого влияния описывается так:

• q — заряд частицы;
• E — напряжённость внутреннего электрического поля.

Когда разность потенциалов уравновешивает магнитное поле, система считается стабильной. При этом соблюдается условие F_л= F_эл. Следовательно, верны и два следующих утверждения:

Скорость электронов обычно определяется с помощью формулы плотности тока:

• q — заряд частицы;
• n — кол-во частиц на единицу объёма.

Теперь электрическое поле E можно описать с помощью выражения:

Найдём разность потенциалов:

U_н=dE=djB/qn, где d — толщина проводящей пластины.

Упростить данное выражение можно с помощью так называемой «постоянной Холла», которая имеет вид R=1/qn. Окончательная формула разности потенциалов примет вид:

То есть, разность потенциалов прямо пропорциональна толщине проводника, магнитной индукции и плотности тока.

Применение

Поскольку данное явление позволяет адекватно оценить концентрацию и подвижность заряженных частиц, проследить чёткую зависимость между силой тока, внешним магнитным полем и поведением электронов в материале, он нашёл широкое применение на практике. В общем виде устройства и приборы, принцип действия которых основан на эффекте Холла, можно разделить на две категории: контрольно-измерительное оборудование для материалов с различной проводимостью и электронные датчики.

В проводниках и полупроводниках

В точном машиностроении рассматриваемый эффект используют для определения электромагнитных свойств и молекулярной структуры материала. В проводниках эти показатели оцениваются посредством анализа движения электронов под воздействием силы тока и магнитных полей, в полупроводниках же с равной эффективностью анализируется как поведение электронов, так и образование электронных дырок. Широкое распространение получил метод ван дер Пау, позволяющий определить:

• тип полупроводника (p или n);
• концентрацию заряженных частиц;
• холловскую подвижность заряженных частиц.

Метод применим к любому плоскому образцу произвольной формы, толщина которого намного меньше длины исследуемого участка. Он широко используется при первичных расчётах полупроводниковых приборов: диодов, транзисторов, тиристоров и др.

Направление поля Холла в проводниках зависит от их типа

Датчики Холла — назначение и разновидности

Самостоятельные устройства и элементы систем, использующие интересующий нас эффект для измерения магнитоэлектрических величин, называют датчиками Холла. Их делят на две большие группы: аналоговые и цифровые. Аналоговые датчики очень просты и представляют собой, как правило, изолированный источник магнитного поля, действие которого на проводник напрямую зависит от расстояния и полярности. Такие датчики служат для преобразования магнитной индукции в разность потенциалов.

Они необходимы для измерения магнитных полей. Если индукция поля превышает заданный порог срабатывания датчика, то он формирует цифровой сигнал «1», в противном случае значение сигнала – «0». Ввиду наличия «слепых зон», в которых индукция слишком мала для срабатывания датчика, его применение не всегда целесообразно. Цифровые датчики холла делят на:

• униполярные — генерируют выходной сигнал в магнитном поле любой полярности, отключаются при падении индукции;
• биполярные — переключают выходной сигнал с «1» на «0» при изменении полярности магнитного поля.

Датчики Холла встречаются в почти любой достаточно сложной электронике — от бесконтактных выключателей до смартфонов, от автомобильных двигателей до ионных двигателей космических кораблей. Способность реагировать на появление и изменение магнитных полей сделала устройство незаменимым в электронике и электромеханике, а отсутствие прямого физического взаимодействия обеспечило высокую надёжность и точность, износостойкость и долговечность датчиков.

Изготовление датчика тока на основе эффекта Холла

Если Вы обладаете хотя бы базовыми навыками в работе с электронными компонентами, то без особого труда сможете самостоятельно сконструировать датчик тока. С его помощью можно будет бесконтактно определять наличие электрического тока в проводнике. Вот полный перечень материалов и инструментов, которые Вам понадобятся:

• цифровой датчик Холла в «транзисторном» корпусе, например, A3144 или US1881;
• ферритовое кольцо внешним диаметром не менее 25 мм (можно купить в магазине радиодеталей или извлечь из старого блока питания от энергосберегающих ламп или ПК);
• электрический зажим типа «крокодил»;
• цианакрилатный клей;
• резистор и конденсатор номиналами соответственно 10 кОм и 0,1 мкФ;
• плата Arduino, макетная плата, провода — для временной макетной сборки;
• плата Arduino, припой, канифоль, паяльник, провода — для сборки навесным монтажом;
• ручной лобзик с набором пилок, надфили, наждачная бумага, кусочки резины или ветоши.

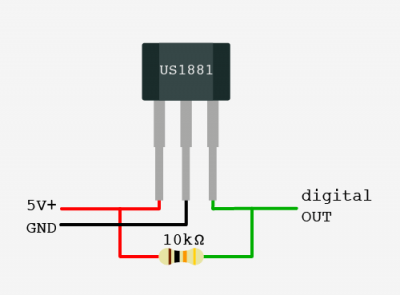
Разверните корпус датчика маркировкой к себе. Нумерация выводов слева направо классическая: 1, 2, 3. Между первой и второй ножкой установите керамический конденсатор ёмкостью 0,1 мкФ (100 нФ). Между первой и третьей ножкой установите резистор сопротивлением 10 кОм. Теперь подключим датчик к плате Arduino по такой схеме:

• «1» — к контакту 5V+;
• «2» — к контакту GND;
• «3» — к цифровому выходу.

Устанавливать кермачиеский конденсатор между первой и второй ножками необязательно, но рекомендуется для стабилизации входящего напряжения

Ферритовое кольцо аккуратно распилите пополам с помощью ручного лобзика. Материал твёрдый, но достаточно хрупкий, поэтому работать придётся осторожно. Полученные полукольца очистите от сколов и шероховатостей, после чего приклейте сбоку к «челюстям» зажима-крокодила так, чтобы в сжатом состоянии торцы полуколец едва касались друг друга. На один из торцов наклейте кусочек плотной толстой ткани или резины, на второй — корпус цифрового датчика Холла.

Теперь, поместив внутри разрезанного ферритового кольца проводник и пустив по нему электрический ток, вы сможете наблюдать появление входящего сигнала на плате Arduino.

На сегодняшний день классический эффект Холла полностью изучен и служит теоретической базой для более или менее сложных электронных устройств. Ведутся исследования частных разновидностей эффекта Холла, в том числе поиск способов их использования в электрических, жидко- и газотопливных двигателях нового поколения.

Источник