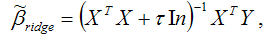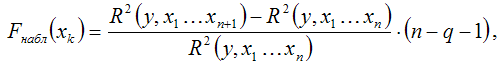Способы преодоления мультиколлинеарности во множественной регрессии

Методы устранения мультиколлинеарности

Если оцененную модель регрессии предполагается использовать для изучения экономических связей, то устранение мультиколлинеарных факторов является обязательным, потому что их наличие в модели может привести к неправильным знакам коэффициентов регрессии.

При построении прогноза на основе модели регрессии с мультиколлинеарными факторами необходимо оценивать ситуацию по величине ошибки прогноза. Если её величина является удовлетворительной, то модель можно использовать, несмотря на мультиколлинеарность. Если же величина ошибки прогноза большая, то устранение мультиколлинеарных факторов из модели регрессии является одним из методов повышения точности прогноза.

К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся:

1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна;

2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:

Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов;

Если рассмотренные способы не помогли устранить мультиколлинеарность факторов, то переходят к использованию смещённых методов оценки неизвестных параметров модели регрессии, или методов исключения переменных из модели множественной регрессии.

Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессию или ридж (ridge).

При использовании метода гребневой регрессии ко всем диагональным элементам матрицы (ХТХ) добавляется небольшое число τ: 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:

где ln – единичная матрица.

Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу.

Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.

Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных x_i (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F. При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных x_i (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.

Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.

Метод пошагового включения осуществляется по следующему алгоритму:

1) из всех факторных переменных в модель регрессии включаются те переменные, которым соответствует наибольший модуль линейного коэффициента парной корреляции с результативной переменной;

2) при добавлении в модель регрессии новых факторных переменных проверяется их значимость с помощью F-критерия Фишера. При том выдвигается основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии. Обратная гипотеза состоит в утверждении о целесообразности включения факторной переменной xk в модель множественной регрессии. Критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. Наблюдаемое значение F-критерия рассчитывается по формуле:

где q – число уже включённых в модель регрессии факторных переменных.

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии отвергается. Следовательно, включение данной переменной в модель множественной регрессии является обоснованным.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии принимается. Следовательно, данную факторную переменную можно не включать в модель без ущерба для её качества

3) проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие Fнабл›Fкрит.

Источник

Методы отбора факторов при построении множественных регрессионных моделей. Мультиколлинеарность факторов, способы её устранения

Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

— шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты — отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).
В процедуре отсева факторов наиболее широко используется матрица частных коэффициентов корреляции.

При отборе факторов рекомендуется, кроме всего прочего, пользоваться следующим правилом: число включаемых факторов должно быть в 6-7 раз меньше объема совокупности, по которой строится регрессия.

Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в реализации алгоритмов последовательного «включения», «исключения» или «включения-исключения» факторов в уравнение регрессии и последующей проверке их статистической значимости.

Наличие мультиколлинеарности между признаками вызывает:

— искажению величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков;

— изменению смысла экономической интерпретации коэффициентов регрессии.

Для устранения мультиколлинеарности используется метод исключения переменных. Этот метод заключается в том, что высоко коррелированные объясняющие переменные (факторы) устраняются из регрессии и она заново оценивается. Отбор переменных, подлежащих исключению, производится с помощью коэффициентов парной корреляции. Опыт показывает, что если \ryj\ > 0,70, то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия.

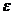
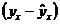
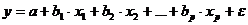
37) При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей. , которая представляет собой в уравнении ненаблюдаемую величину.

Исследования остатков предполагают проверку наличия сле­дующих пяти предпосылок МНК:

1) случайный характер остатков. С этой целью строится график отклонения остатков от теоретических значений признака. Если на графике получена горизонтальная полоса, то остатки представляют собой случайные величины и применение МНК оправдано. В других случаях необходимо применить либо другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки не будут случайными величинами.

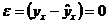
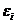
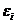
2) нулевая средняя величина остатков, т.е. , не зависящая от хi. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю­чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков от теоретических значений ре­зультативного признака ух строится график зависимости случай­ных остатков от факторов, включенных в регрессию хi . Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xj. Если же график показывает наличие зависимости и хjто модель неадек­ватна. Причины неадекватности могут быть разные.

3. Гомоскедастичность — дисперсия каждого отклонения 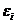одинакова для всех значений хj. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.

4. Отсутствие автокорреляции остатков. Значения остатков 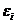распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии.

5. Остатки подчиняются нормальному распределению.

В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков 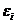не соответствует некоторым предпосылкам МНК, то следует корректировать модель, изменить ее спецификацию, добавить (исключить) некоторые факторы, преобразовать исходные данные, что в конечном итоге позволяет получить оценки коэффициентов регрессии aj, которые обладают свойством несмещаемости, имеют меньшее значение дисперсии остатков, и в связи с этим более эффективную статистическую проверку значимости параметров регрессии.

Источник

Регрессионный анализ — множественная регрессия в условиях мультиколлинеарности

Вы будете перенаправлены на Автор24

Понятие и сущность мультиколлинеарности (частичной коллинеарности)

Множественная регрессия представляет собой эконометрическую модель, которая оформлена в виде уравнения, включающего одну эндогенную (зависимую, результативную) переменную и несколько экзогенных (независимых, факторных, объясняющих) переменных.

Как правило, модель множественной регрессии выстраивают на основе метода наименьших квадратов. Однако его применение зачастую оборачивается для исследователей столкновением с достаточно серьёзной проблемой. Эта проблема проявляется в мультиколлинеарности.

Мультиколлинеарность модели множественной регрессии представляет собой наличие высокой взаимной статистической зависимости между факторными переменными.

Вообще в эконометрике выделяют две основные разновидности коллинеарности:

• полная коллинеарность, которая заключается в наличие между факторами функциональной (тождественной) линейной зависимости (наибольшей корреляции);
• частичная коллинеарность (или мультиколлинеарность), которая заключается в наличии между факторами сильной (но не полной) корреляции.

Отрицательные последствия коллинеарности факторов проявляются в том, что параметры в модели множественной регрессии (независимо от методов оценки) оказываются неопределёнными или неустойчивыми. Неопределённость значений параметров регрессионной модели характерна для полной коллинеарности.

Неустойчивость оценок параметров регрессионной модели характерна для частичной коллинеарности (мультиколлинеарности). Это находит выражение в увеличении дисперсии оценок, что означает сильное различие конкретных результатов оценок при однородных выборках. В связи с этим усложняется задача по интерпретации влияния тех или иных факторов на изучаемый объект.

Готовые работы на аналогичную тему

В то же время регрессионная модель, в которой существует мультиколлинеарность, может признаваться статистически значимой. То есть качество множественной регрессии будет считаться высоким даже тогда, когда все коэффициенты являются незначимыми. В этом случае дальнейшая стратегия проведения эконометрического исследования зависит от его основной цели.

Мультиколлинеарность в модели множественной регрессии может быть обнаружена, если в её отношении будет определено, что:

• стандартные ошибки оценок параметров модели имеют большие значения;
• t-статистики имеют маленькие значения, что говорит о незначимости коэффициентов;
• у оценок параметров неправильные знаки, несмотря на статистическую значимость всей модели;
• в условиях достаточно однородной выборки оценки параметров сильно изменяются в результате добавления (или удаления) выборочных данных.

О наличии мультиколлинеарности в регрессионной модели свидетельствуют слишком высокие значения показателя VIF = 1 / (1 – R^2), где R^2 – это коэффициенты детерминации регрессий факторов на остальные факторы.

Если моделирование было нацелено на прогнозирование будущих значений зависимой переменной, то наличие мультиколлинеарности при условии достаточно большого коэффициента детерминации (то есть R^2 больше или равно 0,85) не окажет какого-нибудь значимого влияния на качество прогноза.

Методы устранения (уменьшения) мультиколлинеарсти модели множественной регрессии

Мультиколлинеарность необходимо устранить в случае проведения исследования в целях определения степени воздействия каждого из факторов на итоговый результат, поскольку зависимость между переменными будет представлена в значительно искаженном виде. Тогда исследователю необходимо воспользоваться специально выведенным и практически обработанным методом устранения или уменьшения мультиколлинеарсти.

На нынешний момент в эконометрической науке ещё нет общепринятого мнения насчёт того, каким образом действовать в подобной ситуации. Каждый исследователь сам выбирает способ нивелирования взаимозависимости факторных переменных. Наибольшей популярностью сейчас пользуются следующие методы:

• метод преобразования переменных модели, или метод главных компонент – он заключается в переходе от исходных переменных, связанных тесной корреляционной связью, к новым (ортогональным) переменным, которые между собой слабо коррелированны или вообще не коррелированны;
• метод регуляризации, или метод вычисления смещенных оценок – он заключается в том, что исходная система эконометрических уравнений множественной регрессии заменяется на «регуляризированную» систему, в которую введён параметр регуляризации, чей отбор требует априорной информации о точности задания вектора зависимой переменной;
• метод отбора наиболее информативных объясняющих переменных модели и несвязанных при этом друг с другом – будет эффективен, если первоначальный отбор был проведен не тщательно и не были выявлены все существующие переменные.

Таким образом, в процессе моделирования сложных экономических объектов и явлений, которые могут быть описаны только системами уравнений множественной регрессии, может возникнуть мультиколлинеарность, то есть взаимная зависимость факторных показателей. Она может как осложнить процесс исследования (тогда приходится использовать специальные методы), так и не оказать существенного влияния на итоговые результаты. Это определяется целю проведения эконометрического исследования.

Источник