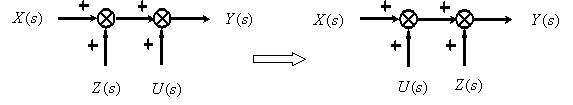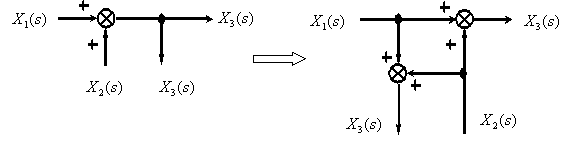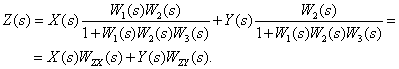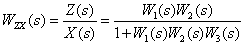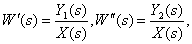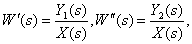Способы преобразования структурных схем тау

Правила эквивалентных преобразований структурных схем систем автоматического управления

Выше были рассмотрены математические модели отдельных динамических звеньев. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. Рассмотрим структуру типичной САУ

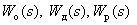
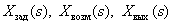
где передаточные функции соответственно объекта, датчика и регулятора, изображения задающего, возмущающего и выходного сигналов.

В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ.

Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ.

Решением этих задач мы и займемся в дальнейшем.

Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения).

Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией.

Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции:

Последовательное соединение динамических звеньев.

Параллельное соединение динамических звеньев.

Замкнутый контур с отрицательной обратной связью.

Замкнутый контур с положительной обратной связью.

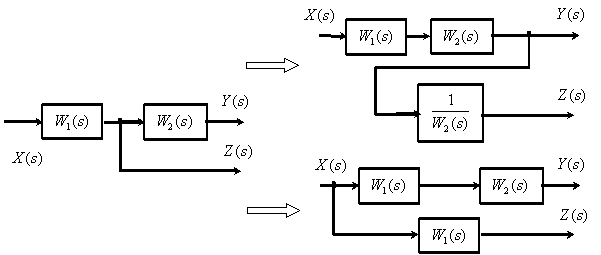
Перенос точки ветвления через динамическое звено.

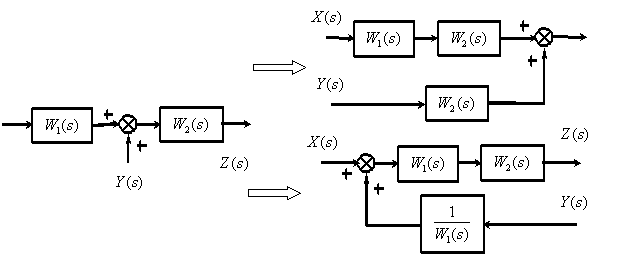
Перенос суммирующего звена через динамическое звено.

Перестановка суммирующих звеньев.

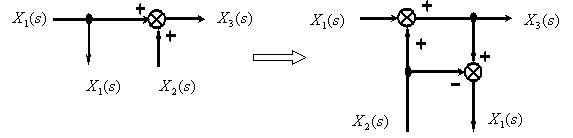
Перенос точки ветвления с выхода на вход суммирующего звена.

Перенос точки ветвления с входа на выход суммирующего звена.

Принцип суперпозиции (наложения)

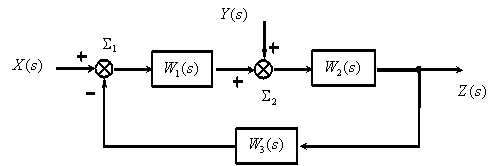
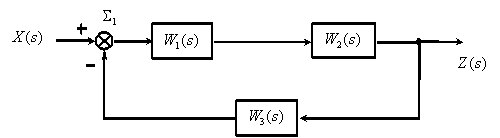
Применим рассмотренные правила для упрощения структурной схемы

Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.

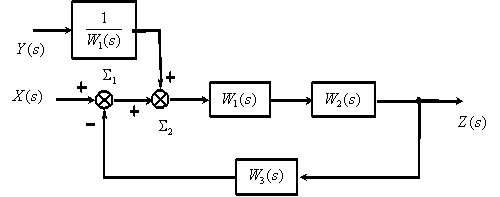
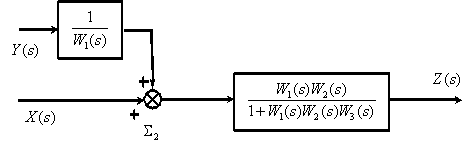
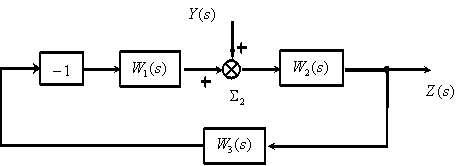
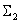
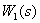
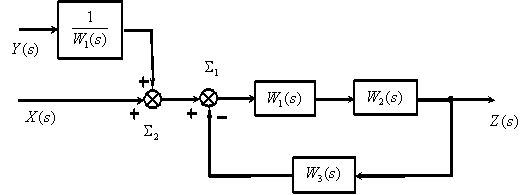
Перенесем суммирующее звено через динамическое звено .

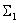
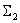
Поменяем местами суммирующие звенья и.

Преобразуем последовательно включенные динамические звенья и .

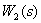
Преобразуем замкнутый контур с отрицательной обратной связью ().

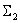
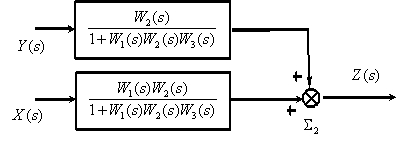
Перенесем суммирующее звено вправо.

Преобразуем последовательно включенные звенья..

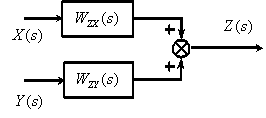
В соответствии с полученной структурной схемой запишем операторное уравнение

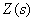
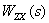
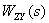
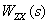
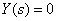
Уравнение показывает, что является линейной комбинацией изображений входных сигналов, взятых с коэффициентами и . Выясним смысл этих коэффициентов на примере коэффициента . Для этого положим в (1) , тогда получим

Таким образом, из (2) следует, это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме , равны нулю.

Теперь становится ясным смысл и самого операторного уравнения (1), описывающего систему. Он заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.

По сути это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.

Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.

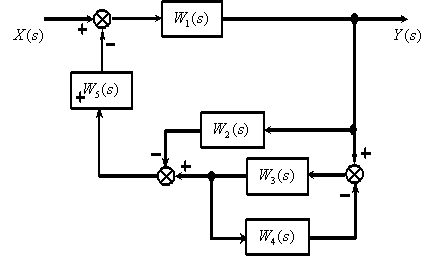
Рассмотрим использование принципа суперпозиции на примере показанной на рис. 1 структурной схемы.

Полагаем 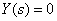и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим

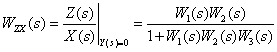
Полагаем 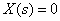и изобразим соответствующую этому случаю структурную схему.

Используя эквивалентные преобразования, получим

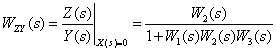
Имея 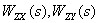, в соответствии с принципом суперпозиции получим «свернутую» структурную схему САУ.

Контрольные вопросы и задачи

Какие задачи позволяют решать правила эквивалентных преобразований структурных схем?

Дайте определение принципа суперпозиции применительно к структурным схемам систем автоматического управления.

Как используют принцип суперпозиции на практике?

Определите передаточные функции

по следующей структурной схеме

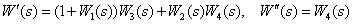
Определите передаточную функцию, эквивалентную структурной схеме.

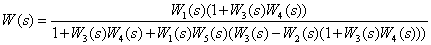
Определите передаточные функции

по следующей структурной схеме

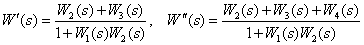
Источник

Способы преобразования структурных схем тау

4.1. Эквивалентные преобразования структурных схем

Структурная схема САУ в простейшем случае строится из элементарных динамических звеньев. Но несколько элементарных звеньев могут быть заменены одним звеном со сложной передаточной функцией. Для этого существуют правила эквивалентного преобразования структурных схем. Рассмотрим возможные способы преобразований.

1. Последовательное соединение (рис.28) — выходная величина предшествующего звена подается на вход последующего. При этом можно записать:

y ₁ = W ₁ y o ; y ₂ = W ₂ y ₁ ; . ; y _n = W _n y _{n — 1} = >

y _n = W 1 W 2 . W n .y o = W_эквy o ,

где.

То есть цепочка последовательно соединенных звеньев преобразуется в эквивалентное звено с передаточной функцией, равной произведению передаточных функций отдельных звеньев.

2. Параллельно — согласное соединение (рис.29) — на вход каждого звена подается один и тот же сигнал, а выходные сигналы складываются. Тогда:

y = y ₁ + y ₂ + . + y _n = (W ₁ + W ₂ + . + W3)y _o = W_эквy _o ,

где .

То есть цепочка звеньев, соединенных параллельно — согласно, преобразуется в звено с передаточной функцией, равной сумме передаточных функций отдельных звеньев.

3. Параллельно — встречное соединение (рис. 30а) — звено охвачено положительной или отрицательной обратной связью. Участок цепи, по которому сигнал идет в противоположном направлении по отношению к системе в целом (то есть с выхода на вход) называется цепью обратной связи с передаточной функцией W _ос . При этом для отрицательной ОС:

Читайте также: Обычный способ это как

где .

Аналогично: — для положительной ОС.

Если W _oc = 1 , то обратная связь называется единичной (рис.30б), тогда W_экв = W _п /(1 ± W _п ).

Замкнутую систему называют одноконтурной , если при ее размыкании в какой либо точке получают цепочку из последовательно соединенных элементов (рис.31а). Участок цепи, состоящий из последовательно соединенных звеньев, соединяющий точку приложения входного сигнала с точкой съема выходного сигнала называется прямой цепью (рис.31б, передаточная функция прямой цепи W _п = WoW ₁ W ₂ ) . Цепь из последовательно соединенных звеньев, входящих в замкнутый контур называют разомкнутой цепью (рис.46в, передаточная функция разомкнутой цепи W _p = W ₁ W ₂ W ₃ W ₄ ).

Исходя из приведенных выше способов эквивалентного преобразования структурных схем, одноконтурная система может быть представлена одним звеном с передаточной функцией: W_экв = W _п /(1 ± W _p ) — передаточная функция одноконтурной замкнутой системы с отрицательной ОС равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи. Для положительной ОС в знаменателе знак минус. Если сменить точку снятия выходного сигнала, то меняется вид прямой цепи. Так, если считать выходным сигнал y ₁ на выходе звена W ₁ , то W _p = WoW ₁ . Выражение для передаточной функции разомкнутой цепи не зависит от точки снятия выходного сигнала.

Замкнутые системы бывают одноконтурными и многоконтурной (рис.32).Чтобы найти эквивалентную передаточную функцию для данной схемы нужно сначала осуществить преобразование отдельных участков.

Если многоконтурная система имеет перекрещивающиеся связи (рис.33), то для вычисления эквивалентной передаточной функции нужны дополнительные правила:

4. При переносе сумматора через звено по ходу сигнала необходимо добавить звено с передаточной функцией того звена, через которое переносится сумматор. Если сумматор переносится против хода сигнала, то добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим сумматор (рис.34).

Так с выхода системы на рис.34а снимается сигнал

Такой же сигнал должен сниматься с выходов систем на рис.34б:

При подобных преобразованиях могут возникать неэквивалентные участки линии связи (на рисунках они заштрихованы).

5. При переносе узла через звено по ходу сигнала добавляется звено с передаточной функцией, обратной передаточной функции звена, через которое переносим узел. Если узел переносится против хода сигнала, то добавляется звено с передаточной функцией звена, через которое переносится узел (рис.35). Так с выхода системы на рис.35а снимается сигнал

Такой же сигнал снимается с выходов рис.35б:

6. Возможны взаимные перестановки узлов и сумматоров: узлы можно менять местами (рис. 36а); сумматоры тоже можно менять местами (рис.36б); при переносе узла через сумматор необходимо добавить сравнивающий элемент (рис.36в: y = y ₁ + f ₁ = > y ₁ = y — f ₁ ) или сумматор (рис.36г: y = y ₁ + f ₁ ).

Во всех случаях переноса элементов структурной схемы возникают неэквивалентные участки линии связи, поэтому надо быть осторожным в местах съема выходного сигнала.

При эквивалентных преобразованиях одной и той же структурной схемы могут быть получены различные передаточные функции системы по разным входам и выходам. Так на рис.48 имеется два входа: по управляющему воздействию u и возмущению f при одном выходе y . Такая схема может быть преобразована к одному звену с двумя передаточными функциями W _uy и W _fy .

4.2. САР напряжения генератора постоянного тока

Для примера рассмотрим схему САР напряжения генератора постоянного тока (рис.37).

Выведем дифференциальное уравнение исполнительного двигателя постоянного тока. Его схема замещения изображена на рис. 38.

Для якорной цепи справедливо уравнение

Если принять, что , гдеj – угол поворота вала двигателя, то

где – постоянная времени якорной цепи; , – коэффициенты пропорциональнсти.

Если учесть, что , где J – момент инерции якоря, M — электромагнитный момент, М _с – момент сторонних сил, то получим

= >

Здесь – электромеханическая постоянная времени;

; ; ; – коэффициенты пропорциональности;

, – передаточные функции по напряжению и моменту сторонних сил.

Структурная схема двигателя постоянного тока показана на рис.39.

Аналогичным образом выводится передаточная функция генератора постоянного тока, которая с учетом пренебрежения индуктивностью обмотки якоря имеет вид, показанный на рис.40, где

Усилитель можно представить пропорциональным звеном с коэффициентом усиления K _у . В окончательном виде структурная схема САР напряжения генератора постоянного тока показана на рис.41.

Перечислите типичные схемы соединения звеньев САУ?
Как преобразовать цепь последовательно соединенных звеньев к одному звену?
Как преобразовать цепь параллельно соединенных звеньев к одному звену?
Как преобразовать обратную связь к одному звену?
Что называется прямой цепью САУ?
Что называется разомкнутой цепью САУ?
Как перенести сумматор через звено по ходу и против движения сигнала?
Как перенести узел через звено по ходу и против движения сигнала?
Как перенести узел через узел по ходу и против движения сигнала?
Как перенести сумматор через сумматор по ходу и против движения сигнала?
Как перенести узел через сумматор и сумматор через узел по ходу и против движения сигнала?
Что называется неэквивалентными участками линий связи в структурных схемах?
Каково назначение САР напряжения генератора постоянного тока?

Источник