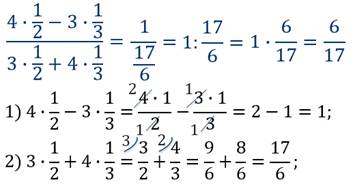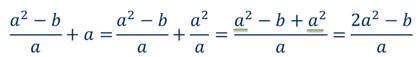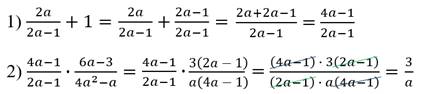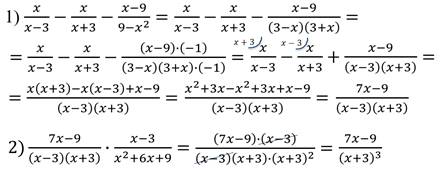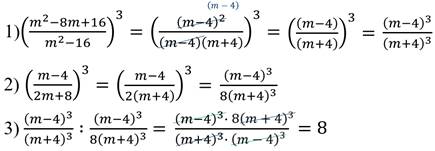Способы преобразования рациональных выражений 8 класс

Грамотное преобразование рациональных выражений

Рациональные выражения и дроби — краеугольный пункт всего курса алгебры. Те, кто научатся работать с такими выражениями, упрощать их и раскладывать на множители, по сути смогут решить любую задачу, поскольку преобразование выражений — неотъемлемая часть любого серьёзного уравнения, неравенства и даже текстовой задачи.

В этом видеоуроке мы посмотрим, как грамотно применять формулы сокращённого умножения для упрощения рациональных выражений и дробей. Научимся видеть эти формулы там, где, на первый взгляд, ничего нет. Заодно повторим такой нехитрый приём, как разложение квадратного трёхчлена на множители через дискриминант.

Как вы уже наверняка догадались по формулам за моей спиной, сегодня мы будем изучать формулы сокращенного умножения, а, точнее, не сами формулы, а их применение для упрощения и сокращения сложных рациональных выражений. Но, прежде чем переходить к решению примеров, давайте познакомимся ближе с этими формулами или вспомним их:

Еще хотел бы отметить, что наша школьная система образования устроена таким образом, что именно с изучением этой темы, т.е. рациональных выражений, а также корней, модулей у всех учеников возникает одна и та же проблема, которую я сейчас объясню.

Дело в том, что в самом начале изучения формул сокращенного умножения и, соответственно, действий по сокращению дробей (это где-то 8 класс) учителя говорят что-то следующее: «Если вам что-то непонятно, то вы не переживайте, мы к этой теме еще вернемся неоднократно, в старших классах так точно. Мы это еще разберем». Ну а затем на рубеже 9-10 класса те же самые учителя объясняют тем же самым ученикам, которые так и не знают, как решать рациональные дроби, примерно следующее: «А где вы были предыдущие два года? Это же изучалось на алгебре в 8 классе! Чего тут может быть непонятного? Это же так очевидно!».

Однако обычным ученикам от таких объяснений нисколько не легче: у них как была каша в голове, так и осталась, поэтому прямо сейчас мы разберем два простых примера, на основании которых и посмотрим, каким образом в настоящих задачах выделять эти выражения, которые приведут нас к формулам сокращенного умножения и как потом применять это для преобразования сложных рациональных выражений.

Сокращение простых рациональных дробей

Задача № 1

Первое, чему нам нужно научиться — выделять в исходных выражениях точные квадраты и более высокие степени, на основании которых мы сможем потом применять формулы. Давайте посмотрим:

Перепишем наше выражение с учетом этих фактов:

Задача № 2

Переходим ко второй задаче:

Упрощать тут нечего, потому что в числителе стоит константа, но я предложил эту задачу именно для того, чтобы вы научились раскладывать на множители многочлены, содержащие две переменных. Если бы вместо него был написанный ниже многочлен, как бы мы разложили его?

Давайте решим уравнение и найдем $x$, которые мы сможем поставить вместо точек:

\[D=25-4\cdot \left( -6 \right)=25+24=49\]

Мы можем переписать трехчлен следующим образом:

С квадратным трехчленом мы работать научились — для этого и нужно было записать этот видеоурок. А что делать, если кроме $x$ и константы присутствует еще $y$? Давайте рассмотрим их как еще одни элементы коэффициентов, т.е. перепишем наше выражение следующим образом:

Запишем разложение нашей квадратной конструкции:

\[\left( x-y \right)\left( x+6y \right)\]

Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:

Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати. Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители.

Нюансы решения

Запомните основные правила преобразования рациональных выражений:

• Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант.
• Работать нужно по такому алгоритму: когда мы смотрим и пытаемся выделить формулу сокращенного умножения, то, прежде всего, пытаемся все перевести в максимально возможную степень. После этого выносим за скобку общую степень.
• Очень часто будут встречаться выражения с параметром: в качестве коэффициентов будут возникать другие переменные. Их мы находим по формуле квадратного разложения.

Таким образом, как только вы видите рациональные дроби, первое, что нужно сделать — это разложить и числитель, и знаменатель на множители (на линейные выражения), при этом мы используем формулы сокращенного умножения или дискриминант.

Давайте посмотрим на пару таких рациональных выражений и попробуем их разложить на множители.

Решение более сложных примеров

Задача № 1

Переписываем и стараемся разложить каждое слагаемое:

\[6xy=2\cdot 3\cdot x\cdot y=2x\cdot 3y\]

Давайте перепишем все наше рациональное выражение с учетом этих фактов:

Источник

Преобразование рациональных выражений

Урок 7. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Преобразование рациональных выражений»

Любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение. Точно также состоит дело и с рациональными выражениями. Любое рациональное выражение после выполнения преобразований принимает вид рациональной дроби. Для этого рациональные выражения предварительно преобразуют или упрощают.

Преобразование рациональных выражений – это применение тождественных преобразований, с целью упростить запись выражения (сделать его короче и удобнее для дальнейших вычислений).

Напомню тождественные преобразования, которые мы уже умеем выполнять:

— приведение подобных слагаемых;

— разложение на множители;

— приведение рациональных дробей к общему знаменателю.

Для преобразования рациональных выражений принимают тот же порядок выполнения действий, что и при преобразовании числовых выражений. Т.е. первыми выполняют действия в скобках, вторыми – действия второй ступени (это умножение, деление, возведение в степень), а затем уже действия первой ступени (сложение, вычитание).

Ещё для преобразования рациональных выражений необходимы знания формул сокращённого умножения и тождества, которые доказали на прошлых уроках:

Задание 1: преобразуйте выражение в рациональную дробь .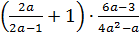

Задание 2: упростите выражение .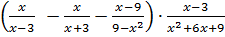

Задание 3: доказать тождество .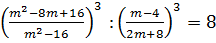

Решение: доказать тождество – это значит установить, что при всех допустимых значениях переменных его левая и правая части равны. Есть несколько способов доказательства тождеств:

1) Можно преобразовать левую часть и в итоге получить правую.

2) Можно преобразовать правую часть и в итоге получить левую.

3) Можно по отдельности преобразовать правую и левую части и в итоге получить и в первом и во втором случае одно и то же выражение.

4) Можно составить разность левой и правой частей и в результате её преобразований должны получить нуль.

Какой способ выбрать зависит от конкретного тождества, которое требуется доказать.

Преобразование рациональных выражений – это применение тождественных преобразований, с целью упростить запись выражения.

Есть несколько способов доказательства тождеств:

1) Можно преобразовать левую часть и в итоге получить правую.

2) Можно преобразовать правую часть и в итоге получить левую.

3) Можно по отдельности преобразовать правую и левую части и в итоге получить и в первом и во втором случае одно и то же выражение.

4) Можно составить разность левой и правой частей и в результате её преобразований должны получить нуль.

Источник

Преобразование рациональных выражений: виды преобразований, примеры

Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.

Определение и примеры рациональных выражений

Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.

Для примера имеем, что 5 , 2 3 · x — 5 , — 3 · a · b 3 — 1 c 2 + 4 a 2 + b 2 1 + a : ( 1 — b ) , ( x + 1 ) · ( y — 2 ) x 5 — 5 · x · y · 2 — 1 11 · x 3 .

То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.

Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.

Основные виды преобразований рациональных выражений

Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.

Преобразовать рациональное выражение 3 · x x · y — 1 — 2 · x x · y — 1 .

Видно, что такое рациональное выражение – это разность 3 · x x · y — 1 и 2 · x x · y — 1 . Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид

3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 · 3 — 2 = x x · y — 1

Ответ: 3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 .

Выполнить преобразование 2 · x · y 4 · ( — 4 ) · x 2 : ( 3 · x — x ) .

Первоначально выполняем действия в скобках 3 · x − x = 2 · x . Данное выражение представляем в виде 2 · x · y 4 · ( — 4 ) · x 2 : ( 3 · x — x ) = 2 · x · y 4 · ( — 4 ) · x 2 : 2 · x . Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.

Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2 · x · y 4 · ( — 4 ) · x 2 : 2 · x = 2 · x · y 4 · ( — 4 ) · x 2 : 2 : x .

Группируем числовые множители с переменной x , после этого можно выполнять действия со степенями. Получаем, что

2 · x · y 4 · ( — 4 ) · x 2 : 2 : x = ( 2 · ( — 4 ) : 2 ) · ( x · x 2 : x ) · y 4 = — 4 · x 2 · y 4

Ответ: 2 · x · y 4 · ( — 4 ) · x 2 : ( 3 · x — x ) = — 4 · x 2 · y 4 .

Преобразовать выражение вида x · ( x + 3 ) — ( 3 · x + 1 ) 1 2 · x · 4 + 2 .

Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида ( x · ( x + 3 ) — ( 3 · x + 1 ) ) : 1 2 · x · 4 + 2 , причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x · ( x + 3 ) — ( 3 · x + 1 ) 1 2 · x · 4 + 2 = x 2 + 3 · x — 3 · x — 1 1 2 · 4 · x + 2 = x 2 — 1 2 · x + 2 .

Преобразуем в числителе формулу разности квадратов, тогда получаем, что

x 2 — 1 2 · x + 2 = ( x — 1 ) · ( x + 1 ) 2 · ( x + 1 ) = x — 1 2

Ответ: x · ( x + 3 ) — ( 3 · x + 1 ) 1 2 · x · 4 + 2 = x — 1 2 .

Представление в виде рациональной дроби

Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.

Представить в виде рациональной дроби a + 5 a · ( a — 3 ) — a 2 — 25 a + 3 · 1 a 2 + 5 · a .

Данное выражение можно представить в виде a 2 — 25 a + 3 · 1 a 2 + 5 · a . Умножение выполняется в первую очередь по правилам.

Следует начать с умножения, тогда получим, что

a 2 — 25 a + 3 · 1 a 2 + 5 · a = a — 5 · ( a + 5 ) a + 3 · 1 a · ( a + 5 ) = a — 5 · ( a + 5 ) · 1 ( a + 3 ) · a · ( a + 5 ) = a — 5 ( a + 3 ) · a

Производим представление полученного результата с исходное. Получим, что

a + 5 a · ( a — 3 ) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a — 3 — a — 5 a + 3 · a

Теперь выполняем вычитание:

a + 5 a · a — 3 — a — 5 a + 3 · a = a + 5 · a + 3 a · ( a — 3 ) · ( a + 3 ) — ( a — 5 ) · ( a — 3 ) ( a + 3 ) · a · ( a — 3 ) = = a + 5 · a + 3 — ( a — 5 ) · ( a — 3 ) a · ( a — 3 ) · ( a + 3 ) = a 2 + 3 · a + 5 · a + 15 — ( a 2 — 3 · a — 5 · a + 15 ) a · ( a — 3 ) · ( a + 3 ) = = 16 · a a · ( a — 3 ) · ( a + 3 ) = 16 a — 3 · ( a + 3 ) = 16 a 2 — 9

После чего очевидно, что исходное выражение примет вид 16 a 2 — 9 .

Ответ: a + 5 a · ( a — 3 ) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 — 9 .

Представить x x + 1 + 1 2 · x — 1 1 + x в виде рациональной дроби.

Заданное выражение записывается как дробь, в числителе которой имеется x x + 1 + 1 , а в знаменателе 2 · x — 1 1 + x . Необходимо произвести преобразования x x + 1 + 1 . Для этого нужно выполнить сложение дроби и числа. Получаем, что x x + 1 + 1 = x x + 1 + 1 1 = x x + 1 + 1 · ( x + 1 ) 1 · ( x + 1 ) = x x + 1 + x + 1 x + 1 = x + x + 1 x + 1 = 2 · x + 1 x + 1

Следует, что x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 x + 1 2 · x — 1 1 + x

Получившаяся дробь может быть записана как 2 · x + 1 x + 1 : 2 · x — 1 1 + x .

После деления придем к рациональной дроби вида

2 · x + 1 x + 1 : 2 · x — 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x — 1 = 2 · x + 1 · ( 1 + x ) ( x + 1 ) · ( 2 · x — 1 ) = 2 · x + 1 2 · x — 1

Можно решить это иначе.

Вместо деления на 2 · x — 1 1 + x производим умножение на обратную ей 1 + x 2 · x — 1 . Применим распределительное свойство и получаем, что

x x + 1 + 1 2 · x — 1 1 + x = x x + 1 + 1 : 2 · x — 1 1 + x = x x + 1 + 1 · 1 + x 2 · x — 1 = = x x + 1 · 1 + x 2 · x — 1 + 1 · 1 + x 2 · x — 1 = x · 1 + x ( x + 1 ) · 2 · x — 1 + 1 + x 2 · x — 1 = = x 2 · x — 1 + 1 + x 2 · x — 1 = x + 1 + x 2 · x — 1 = 2 · x + 1 2 · x — 1

Ответ: x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 2 · x — 1 .

Источник