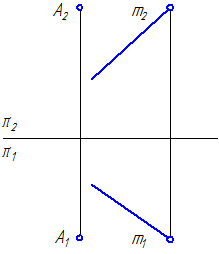Способы преобразования проекций начертательная геометрия

Лекция 4. Способы преобразования ортогонального чертежа

4.1. Способ перемены плоскостей проекций

Чаще всего геометрические объекты расположены относительно плоскостей проекций в общем положении, и при решении задач для достижения поставленной цели необходимо выполнять много построений.

Количество построений можно значительно сократить, если геометрические элементы будут расположены в частном положении относительно плоскостей проекций.

Существуют два основных способа преобразования чертежа, при которых:

1. Объект остаётся неподвижным, при этом меняется аппарат проецирования;
2. Условия проецирования не меняются, но изменяется положение объекта в пространстве.

К первому способу относится способ перемены плоскостей проекций.

Ко второму – способ вращения (вращение вокруг линии уровня и вращение вокруг проецирующей прямой); способ плоскопараллельного перемещения.

Рассмотрим наиболее часто используемые способы при решении задач.

Способ перемены плоскостей проекций или способ введения дополнительных плоскостей проекций (ДПП) позволяет перейти от заданной системы плоскостей проекций к новой системе, более удобной для решения той или иной задачи.

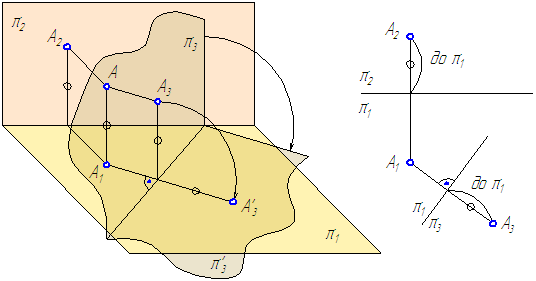
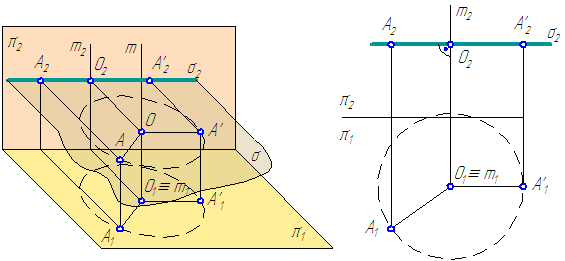
Рассмотрим положение точки А относительно известной системы плоскостей проекций π₂⊥π₁ (Рисунок 4.1, а и б).

Введём π₄⊥π₁, при этом получим новую систему двух взаимно перпендикулярных плоскостей. Положение точки А на эпюре будет в этом случае задано проекциями А₁ и А₄.

Правила перемены плоскостей проекций:

1. Новая плоскость проекций вводится перпендикулярно, по крайней мере, одной из заданных на чертеже плоскостей проекций;
2. ДПП располагается относительно проецируемого объекта в частном положении, удобном для решения поставленной задачи;
3. Новую плоскость совмещаем вращением вокруг новой оси проекций с плоскостью, которой она перпендикулярна на свободное место так, чтобы проекции не накладывались друг на друга.

а б

Рисунок 4.1 – Способ перемены плоскостей проекций

1. На чертеже новая проекция геометрического элемента находится на линии связи, перпендикулярной новой оси проекций:

1. Расстояние от А₄ до π₁/π₄ равно расстоянию от А₂ до π₂/π₁, так как величина этих отрезков (отмечены ○) определяет расстояние от точки А до плоскости проекций π₁.

При решении задачи необходимо заранее обдумать, как расположить новую плоскость проекций относительно заданных геометрических объектов (прямой, плоскости и др.), и как на чертеже провести новую ось проекций, чтобы в новой системе плоскостей заданные объекты заняли бы частные положения по отношению к новой плоскости проекций.

Упражнение

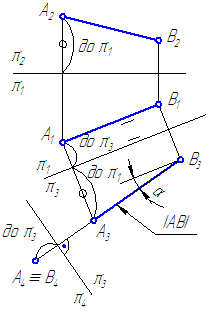
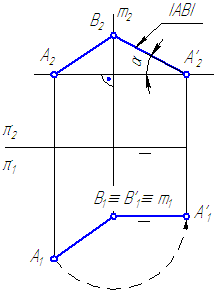
1. Спроецировать отрезок общего положения АВ в точку.

1. Введём ДПП π₄//А₁В₁ и π₄⊥π₁ (Рисунок 4.2). В новой системе двух взаимно перпендикулярных плоскостей проекций π₁/π₄ отрезок АВспроецируется на π₄ в натуральную величину и по этой проекции можем определить угол наклона отрезка к плоскости проекций π₁

Упражнение

2. Дана плоскость общего положения – σ, заданная треугольником АВС (Рисунок 4.3).

Определить истинную величину треугольника.

1. Введём ДПП π₄⊥σ и π₄⊥π₁, для чего построим горизонталь в плоскости треугольника и проведём новую ось проекций π₁/π₄⊥g₁согласно теореме о перпендикуляре к плоскости. На π₄ плоскость σ спроецируется в прямую, что означает σ⊥πp₄.
2. Введём ДПП π₅//σ (π₄/π₅//А₄В₄С₄) и π₄⊥π₅. На π₅ проекция А₅В₅С₅ – есть истинная величина треугольника.

4.2. Способ вращения

Сущность способа вращения состоит в том, что положение системы плоскостей проекций считается неизменным в пространстве, а положение проецируемого объекта относительно неподвижных плоскостей изменяется.

Из сравнения сущности обоих способов видно, что решение задач, которые требуют применения преобразования ортогонального чертежа, может быть выполнено любым из этих способов, результат при этом должен получиться одинаковым. Основа выбора того или иного способа – рациональность решения.

Вращение заданных элементов будем осуществлять вокруг проецирующей прямой, то есть прямой, перпендикулярной какой-либо плоскости проекций, при этом все точки заданных элементов поворачиваются в одну и ту же сторону на один и тот же угол (Рисунок 4.4, а и б). Ось вращения и объект вращения составляют твёрдое тело.

А – точка в пространстве;

О – центр вращения точки А;

АО – радиус вращения

а б

Рисунок 4.4 – Способ вращения вокруг прямой, перпендикулярной π₂

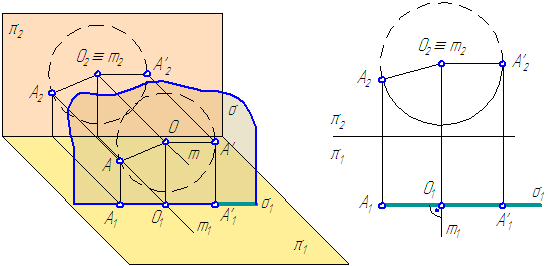
Точка описывает в пространстве окружность радиусом АО. Плоскость окружности перпендикулярна оси вращения (σ⊥m).

Так как m⊥π₂ , то σ//π₂, следовательно, σ⊥π₁, ⇒ σ₁⊥m₁, и поэтому σ проецируется на π₁ в виде прямой, перпендикулярной проекции оси вращения, а на π₂ траектория вращающейся точки проецируется в виде окружности с центром О₂≡m₂.

Пусть ось вращения m⊥π₁ (Рисунок 4.5, а и б). Плоскость окружности σ⊥m.

а б
Рисунок 4.5 – Вращение вокруг прямой, перпендикулярной π₁
\left.\begin\sigma\parallel\pi_1\\\sigma\perp \pi_2\\\end\right\> npu\;m\perp\pi_1\Longrightarrow\sigma_2\perp m_2
Свойства проекций

1. На плоскость проекций, перпендикулярную оси вращения, траектория вращающейся вокруг этой оси точки проецируется без искажения, то есть в окружность с центром, совпадающим с проекцией оси вращения на эту плоскость и радиусом, равным расстоянию от вращаемой точки до оси вращения.
2. На плоскость проекций, параллельную оси вращения, траектория вращающейся точки проецируется в отрезок, перпендикулярный проекции оси вращения на эту плоскость.
3. На плоскость проекций, перпендикулярную оси вращения, проекция вращаемого объекта своих размеров и формы не меняет.

Упражнение

Дано : отрезок общего положения – АВ.

Определить : способом вращения истинную величину отрезка и углы наклона его к плоскостям проекций.

1. Выберем ось вращения m⊥π₁ и проходящую через точку В (Рисунок 4.6).

На плоскости проекций π₂ проекция траектории перемещения точки А – прямая,

A_2 \overline\perp m_2\;u\;A_2\overline\parallel\pi_2/\pi_1

На плоскости проекций π₁ проекция траектории перемещения точки А – окружность радиусом |А₁В₁|.

Повернем отрезок до положения, параллельного плоскости проекций π₂. Получим натуральную величину отрезка.

Угол наклона отрезка АВ к плоскости проекций π₁ будет угол
\alpha=\angle\widehat_2> .

Для того, чтобы определить угол наклона АВ к плоскости проекций π₂, надо ввести новую ось вращения перпендикулярно π₂ и повторить построения.

4.3. Определение истинной величины треугольника способом вращения

Пусть плоскость σ задана треугольником. Необходимо определить истинную величину треугольника (Рисунок 4.7).

Одним поворотом вокруг оси, перпендикулярной к плоскости проекций, истинную форму треугольника получить нельзя (так же как и введением одной ДПП).

Вращая вокруг оси m, перпендикулярной π₁ можно расположить плоскость ΔАВС⊥π₂ (а вращая вокруг оси n⊥π₂ можно расположить плоскость ΔАВС⊥π₁).

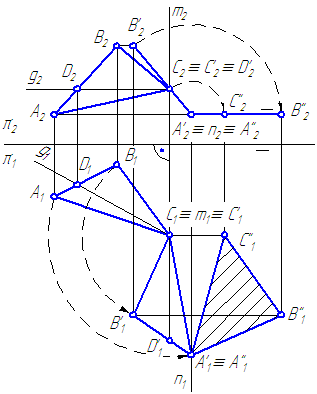
Рисунок 4.7

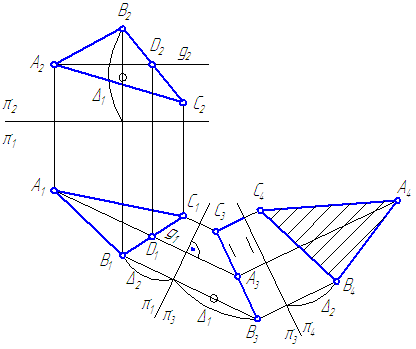
1. Положим σ’ должна быть перпендикулярна π₂. Для чего построим CD – горизонталь h плоскости σ. Введём первую ось вращения m⊥π₁, например, через точку С.
2. Повернём треугольник вокруг m до положения, когда
   \overline\perp\pi_2\Rightarrow\overline_1\overline_1\perp\pi_2/\pi_1
   На основании 3-го свойства, новая горизонтальная проекция треугольника \overline по величине должна равняться A₁B₁C₁, а фронтальная проекция треугольника будет представлять отрезок.
3. Введём вторую ось вращения n⊥π₂ через точку \overline_2 . Повернём фронтальную проекцию \overline в новое положение \overline<\overline\overline\overline>\parallel\pi_2/\pi_1 . На π₁ получим треугольник \overline<\overline\overline\overline> , равный истинной величине треугольника АВС.

4.4. Задачи для самостоятельной работы

Двумя способами преобразования ортогонального чертежа:

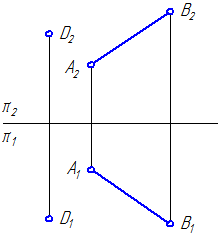
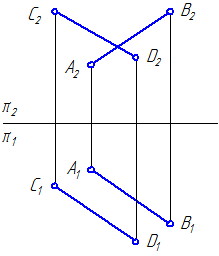
1. Определить расстояние от точки D до отрезка АВ – общего положения (Рисунок 4.8).

Рисунок 4.8

2. Определить расстояние между двумя параллельными прямыми общего положения (АВ//CD) (Рисунок 4.9).

Рисунок 4.9

3. Определить расстояние между двумя скрещивающимися прямыми, заданными отрезками АВ и CD (Рисунок 4.10).

Рисунок 4.10

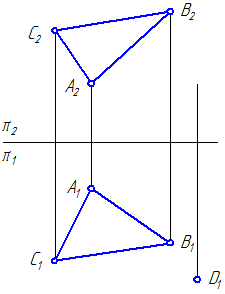
4. Построить недостающую проекцию точки D при условии, что задана σ=ΔАВС – общего положения и первая проекция точки D₁, Dотстоит от плоскости σ на 30 мм (Рисунок 4.11).

Рисунок 4.11

5. Дан отрезок АВ – общего положения. Ось вращения не проходит через АВ (Рисунок 4.12). Определить способом вращения истинную величину АВ.

Рисунок 4.12

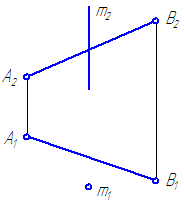
6. Задана прямая общего положения m и точка А вне прямой. Построить плоскость, проходящую через точку А и перпендикулярную прямой m (Рисунок 4.13).

Рисунок 4.13

Источник

Способы преобразования чертежа

Содержание:

Способы преобразования чертежа можно классифицировать, исходя из основных составляющих аппарата проецирования:

• изменение положения фигур относительно основной системы координат (способ вращения относительно различных осей; способ плоскопараллельного движения);
• изменение положения плоскостей проекций (способ замены плоскостей проекций);
• изменение направления проецирования (способы дополнительного проецирования: косоугольное, окружностное, винтовое и другие).

Цель способов преобразования чертежа — приведение геометрических фигур в частное (параллельное или проецирующее) положение относительно плоскостей проекций для обеспечения большей наглядности изображения и упрощения решения позиционных и метрических задач.

Способ замены плоскостей проекций

Смысл способа замены плоскостей проекций: при сохранении неизменного положения фигуры в пространстве вводится новая плоскость проекций, перпендикулярная одной из основных плоскостей проекций; для получения новой проекции фигуры она ортогонально проецируется на введенную плоскость проекций

Проецирование точки на вспомогательную плоскость проекций

Метрические задачи начертательной геометрии связаны с определением натуральных величин геометрических объектов. Эти величины невозможно построить ни на одной из плоскостей проекций П1, П2, П3 для произвольной ориентации объектов в пространстве: проекции отрезков короче, чем их оригиналы; проекции плоских фигур имеют искаженную форму и меньшую площадь: проекции углов, в том числе прямых, не равны действительным их значениям (рис. 2.1).

При решении позиционных задач прямым способом приходится вводить множество вспомогательных геометрических фигур, что приводит к громоздкости геометрических построений. Например, для определения линии пересечения двух плоскостей необходимо вводить вспомогательные плоскости особого положения; для построения двух взаимно перпендикулярных прямых необходимо вводить плоскость общего положения и т.д. (см. раздел 1). Это усложняет решение практических задач и чтение комплексного чертежа.

Проецирование геометрических объектов

Для устранения выше перечисленных проблем применяются способы преобразования комплексного чертежа. Одна группа этих способов связана со сменой ориентации плоскостей проекций относительно данных объектов, вторая – со сменой ориентации геометрических объектов относительно фиксированных плоскостей проекций, третья –со сменой способа проецирования. К первой группе относятся такие способы:

а) способ замены плоскостей проекций;

б) способ прямоугольного аксонометрического проецирования (см. п. 6.4),

в) способ вращения вокруг проецирующей оси (см. п. 2.2);

г) способ плоскопараллельного перемещения (см. п. 2.3);

д) способы вращения вокруг линии уровня (см. п. 2.4),

е) способ косоугольного проецирования (см. п. 2.5).

Все вышеперечисленные способы применяются для перевода геометрических объектов из общего положения в частное (положение уровня или проецирующее положение) с целью установления их взаимного расположения или для определения натуральных величин.

Суть способа замены плоскостей проекций

Способ замены плоскостей проекций состоит во введении системы дополнительных плоскостей особого положения П4, П5, …, параллельных или перпендикулярных элементам заданных геометрических объектов (плоскостей или плоских линий) с дальнейшим проецированием на эти плоскости (рис. 2.2 а, в, д) и совмещением П4, П5, … в одну плоскость (рис. 2.2 б, г, е).

Способ замены плоскостей проекций

На рис. 2.2 а – б построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П4. Плоскость П4 — горизонтально-проецирующая. её горизонтальный след — одна из осей вспомогательной системы координат. Нижний индекс «14» свидетельствует о том, что прямая является линией пересечения плоскостей П1, П4. Вторая ось – фронтальный след – по направлению совпадает с осью z.

На рис. 2.2 в – г построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П5. Плоскость П5 -фронтально-проецирующая. её фронтальный след — одна из осей вспомогательной системы координат. Нижний индекс «25» свидетельствует о том, что прямая является линией пересечения плоскостей П2, П5. Другая ось – горизонтальный след – по направлению совпадает с осью у.

На рис. 2.2 д – е построены четыре ортогональные проекции точки А на плоскости проекций П1, П2, П3, П6. Плоскость П6 — профильно-проецирующая. её профильный след — одна из осей вспомогательной системы координат. Нижний индекс «36» свидетельствует о том, что прямая является линией пересечения плоскостей П3, П6.Другая ось – фронтальный след –по направлению совпадает с осью х.

Правила проецирования на вспомогательные плоскости проекций:

а) проекция А4 точки А на горизонтально-проецирующую плоскость П4 находится на линии проекционной связи А1А4, перпендикулярной оси и сохраняет высоту (координату z);

б) проекция А5 точки А на фронтально-проецирующую плоскость П5 находится на линии проекционной связи А2А5, перпендикулярной оси и сохраняет глубину (координату у);

в) проекция А6 точки А на профильно-проецирующую плоскость П6 находится на линии проекционной связи А3А6,перпендикулярной оси и сохраняет ширину (координату х).

Длина отрезка и углы его наклона к плоскости проекций

Длины проекций отрезка АВ прямой общего положения на плоскости проекций П1, П2, П3 меньше действительной длины отрезка. Только прямые особого положения проецируются хотя бы на одну из плоскостей проекций в натуральную величину.

Для определения натуральной величины отрезка АВ способом замены плоскостей проекций необходимо ввести плоскость П4, параллельную этому отрезку. Проекция А4В4 — натуральная величина (рис. 2.3 а). Угол α наклона отрезка АВ к плоскости П1 равен углу наклона проекции А4В4 к оси .

На рис. 2.3 б заданы горизонтальная и фронтальная проекции отрезка АВ. Для определения натуральной величины отрезка и угла его наклона к плоскости П1 вводится вспомогательная горизонтально-проецирующая плоскость П4, параллельная отрезку АВ (ось параллельна проекции А1В1). С помощью линий проекционной связи и по координатам концов отрезка определяется проекция А4В4, являющаяся натуральной величиной АВ.

Аналогично можно определить натуральную величину отрезка путём введения дополнительной фронтально- или профильно-проецирующей плоскости П5, П6.В этом случае можно определить углы β, γ наклона отрезка к П2, П3 (рис. 2.3 в – г).

Необходимо отметить, что расстояние от отрезка до дополнительной плоскости проекций выбирается произвольно. В п. 1.4.4 показан способ прямоугольного треугольника для определения натуральной величины отрезка. Этот способ является частным случаем способа замены плоскостей проекций, в котором отрезок принадлежит вспомогательной плоскости проекций (расстояние от отрезка до вспомогательной плоскости проекций равно нулю).

Определение натуральной величины отрезка и углов его наклона к плоскостям проекций

Расстояние от точки до прямой и плоскости

Для определения расстояния от точки D до прямой l общего положения (рис. 2.4 а) необходимо ввести вспомогательную плоскость проекций П4, параллельную прямой (ось параллельна проекции l1),и найти проекции D4, l4. В таком случае прямая l занимает положения уровня относительно П4. При дальнейшем введении вспомогательной плоскости проекций П5, перпендикулярной прямой l (ось перпендикулярна проекции l4), последняя проецируется в точку l5, поскольку прямая l занимает проецирующее положения относительно П5. Проекции геометрических объектов на плоскость П5 строятся по координатам, которые определяются по системе плоскостей П1, П4. Например, расстояние h от оси до D5 равно расстоянию от оси до D1. Длина отрезка D5l5 рана расстоянию от точки D до прямой l.

Необходимо отметить, что плоскость П5 нельзя вводить сразу (без использования П4), поскольку она занимает особое положения только в системе плоскостей П4, П5, а в системе П1, П2, П3 – общее.

Определение расстояния от точки до прямой

На рис. 2.4 б прямая l задана отрезком АВ. Отрезок DN принадлежит прямой перпендикулярной l. Прямая занимает положения уровня относительно П5 (проекция D4N4 параллельна оси ). Точка N (основа перпендикуляра) является точкой пересечения двух взаимно перпендикулярных прямых n, l. Таким образом, задачу по определению расстояния от точки D до прямой l способом замены плоскостей проекций можно дополнить задачей на построение двух взаимно перпендикулярных прямых l, n ,пересекающихся в точке N.

Для определения расстояния от точки D до плоскости Σ общего положения (рис. 2.5 а) необходимо перевести плоскость Σ в проецирующее положения путём введения вспомогательной плоскости проекций П4, перпендикулярной Σ (ось перпендикулярна одной из линий уровня плоскости). В этом случае плоскость Σ проецируется в прямую Σ4, а искомое расстояние является длиной перпендикуляра D4N4, проведенного из точки D4 до прямой Σ4. Точка N — основа перпендикуляра и одновременно точка пересечения прямой заданной отрезком DN, с плоскостью Σ.

На рис. 2.5 б плоскость Σ задана треугольником АВС. Его горизонтальная прямая уровня h, заданная двумя точками А и 1, проецируется на перпендикулярную ей плоскость П4 в точку h4. Проекция А4В4С4 треугольника является отрезком, наклонённым под углом α к оси . Этот угол равен углу наклона плоскости Σ к П1. Расстояние от точки D до плоскости АВС равно длине отрезка D4N4. Горизонтальная проекция D1N1 параллельна оси и перпендикулярна горизонтальной проекции h1 горизонтали.

Определение расстояния от точки до плоскости

Расстояние между параллельными прямыми, прямой и плоскостью, двумя плоскостями

Для определения расстояния между параллельными прямыми l, m способом замены плоскостей проекций (рис. 2.6 а) вводится система двух вспомогательных плоскостей проекций П4, П5. Первая из них параллельна заданным прямым, вторая – им перпендикулярна. На плоскость П4 прямые проецируются в натуральные величины, на П5 – в точки . Длина отрезка равна расстоянию между параллельными прямыми l, m.

На рис. 2.6 б прямые заданы отрезками АВ, CD. Отрезок принадлежит прямой , перпендикулярной прямой . Прямая занимает положение уровня относительно П5 (проекция параллельна оси ). Длина отрезка равна расстоянию между параллельными прямыми l, m.

Для определения расстояния между параллельными прямой l и плоскостью Σ (рис. 2.7 а) вводится вспомогательная плоскость проекций П4, перпендикулярна Σ (ось перпендикулярна одной из линий уровня плоскости). Искомое расстояние является длиной отрезка , перпендикулярного проекциям l4, Σ4.

На рис. 2.7 б плоскость Σ задана треугольником АВС. Его горизонтальная прямая уровня h, заданная двумя точками А, 1, проецируется на перпендикулярную ей плоскость П4 в точку h4. Проекция А4В4С4 треугольника является отрезком прямой. Расстояние от прямой l до плоскости АВС равно длине отрезка . Горизонтальная проекция параллельна оси и перпендикулярна горизонтальной проекции h1 горизонтали.

Для определения расстояния между параллельными плоскостями Σ, Ω (рис. 2.8 а) вводится вспомогательная плоскость проекций П4, перпендикулярна этим плоскостям (ось перпендикулярна линии уровня одной из плоскостей). Искомое расстояние является длиной отрезка , перпендикулярного проекциям Σ4, Ω4.

На рис. 2.8 б плоскости Σ, Ω заданы своими горизонтальными и фронтальными следами. Фронтальный след плоскости Σ проецируется на перпендикулярную ей плоскость П4 в точку . Проекции Σ4, Ω4 плоскостей являются прямыми – следами построенными с помощью

Определение расстояния между параллельными прямыми

Определение расстояния между параллельными прямой и плоскостью

Определение расстояния между параллельными плоскостями

Расстояние между скрещивающимися прямыми

Для определения расстояния между скрещивающимися прямыми l, m способом замены плоскостей проекций (рис. 2.9) вводится система двух вспомогательных плоскостей проекций П4, П5. Первая из них параллельна одной из заданных прямых (например, l), вторая – перпендикулярна этой прямой. На плоскость П4 прямая l проецируется в натуральную величину, на П5 – в точку. Длина отрезка равна расстоянию между скрещивающимися прямыми l, m

На рис. 2.9 прямые заданы отрезками АВ, CD. Отрезок перпендикулярен прямым и занимает положения уровня относительно П5 (проекция параллельна оси ). Длина отрезка равна расстоянию между скрещивающимися прямыми l, m.

Определение расстояния между скрещивающимися прямыми

Угол между прямыми, прямой и плоскостью, двумя плоскостями

Натуральную величину углов между прямыми, прямой и плоскостью, двумя плоскостями невозможно определить графически по их проекциям без применения способов преобразования комплексного чертежа.

Для определения плоского угла χ между прямыми l, m, пересекающимися в точке K, способом замены плоскостей проекций необходимо спроецировать этот угол в натуральную величину. Следует ввести систему двух вспомогательных плоскостей проекций П4, П5. Первая должна быть перпендикулярна плоскости Σ, образованной данными прямыми, вторая – параллельна Σ.

На рис. 2.10 прямые l, m заданы отрезками AВ, СD. Плоскость П4 перпендикулярна фронтали f (плоскости Σ), проведенной через точки C, 1. Проекция Σ4 является отрезком прямой линии. Плоскость П5 параллельна плоскости Σ (проекция Σ4 параллельна оси ).

Определение плоского угла

Угол φ между прямой l и плоскостью Σ определяется с помощью введения вспомогательной плоскости проекций П4, перпендикулярный заданной плоскости (рис. 2.11 а). Таким образом, задача по определению угла φ между прямой l и плоскостью Σ сводится к задаче по определению угла между проекцией l4 прямой и следом Σ4 плоскости.

Угол φ между прямой l и плоскостью Σ также определяется (рис. 2.11 б) с помощью вспомогательного угла между данной прямой и прямой проходящей через произвольную точку D прямой l перпендикулярно плоскости Σ (см. п. 1.6.3, рис. 1.69). Таким образом, задача по определению угла φ между прямой l и плоскостью Σ сводится к задаче по определению вспомогательного угла между двумя прямыми (см. рис. 2.10). Из проекций D1, D2 произвольной точки прямой l проведены проекции перпендикулярные соответствующим следам плоскости Σ. С помощью вспомогательной плоскости проекций П4, перпендикулярной плоскости Ω, образованной прямыми (ось перпендикулярна проекции h1 плоскости Ω), последняя проецируется в прямую линию l4. После введения плоскости проекций П5, параллельной плоскости Ω (ось параллельна следу l4), определяется натуральная величина вспомогательного угла . Искомый угол φ дополняет вспомогательный угол до 90°.

Определение угла между прямой и плоскостью

Существуют два способа определения угла θ между двумя плоскостями Σ, Ω (см. п. 1.6.3). Прямой способ реализуется, в том числе, с помощью способа замены плоскостей проекций.

Прямой способ определения двугранного угла

На рис. 2.12 плоскости Σ, Ω заданы треугольником АВС и параллельными прямыми a, b. Прямая k — линия пересечения плоскостей (см. п. 1.5.8, рис. 1.42). С помощью вспомогательной плоскости проекций П4, параллельной прямой k, последняя переведена в положения уровня. Введение плоскости проекций П5, перпендикулярной прямой k, позволяет определить угол θ между заданными плоскостями.

При непрямом способе угол θ между плоскостями Σ, Ω равен углу между прямыми пересекающимися в произвольной точке пространства и перпендикулярны ,соответственно, плоскостям Σ, Ω (см. п. 1.6.3, рис. 1.70)..

На рис. 2.13 плоскости Σ, Ω заданы своими горизонтальными и фронтальными следами. Из проекций D1, D2 произвольной точки пространства проведены прямые и перпендикулярные соответствующим следам плоскостей.

С помощью вспомогательной плоскости проекций П4, перпендикулярной вспомогательной плоскости Ψ, заданной прямыми плоскость Ψ переведена в проецирующее положение. После введения плоскости проекций П5, параллельной плоскости Ψ, определяется угол , числовое значение которого совпадает с искомым углом θ.

Непрямой способ определения двугранного угла

Натуральная величина плоской фигуры

Натуральная величина плоской фигуры определяется как без применения способов преобразования комплексного чертежа, так и с их применением.

На рис. 2.14 показан способ определения натуральной величины треугольника АВС способом прямоугольного треугольника (см. п. 1.4.4). Предварительно определяются натуральные величины сторон АВ, ВС, АС. На их основе строится треугольник А0В0С0, тождественный натуральной величине треугольника АВС

Для определения натуральной величины плоской фигуры Ф способом замени плоскостей проекций (рис. 2.15 а) необходимо ввести по очереди плоскость П4, перпендикулярную Ф, и П5, параллельную Ф (ось параллельная следу плоской фигуры на плоскости П4). Проекция Ф5 является натуральной величиной фигуры Ф.

На рис. 2.15 б плоская фигура является треугольником АВС. Ось вспомогательной системы плоскостей П1, П4 перпендикулярна фронтальной проекции фронтали f треугольника. Проекция А4В4С4 является отрезком прямой линии. Ось вспомогательной системы плоскостей П4, П5 параллельна проекции А4В4С4. Проекция А5В5С5 является натуральной величиной треугольника АВС.

Определение натуральной величины плоской фигуры способом прямоугольного треугольника

Определение натуральной величины плоской фигуры способом замены плоскостей проекций

Пересечение прямой и плоскости, двух плоскостей

У п. 1.5.7 показан способ определения точки K пересечения прямой l и плоскости Σ с помощью вспомогательной плоскости Ω особого положения (рис. 1.38).

Для определения точки K пересечения прямой l с плоскостью Σ способом замены плоскостей проекций (рис. 2.16) вводится вспомогательная плоскость П4, перпендикулярная плоскости Σ. На П4 последняя проецируется в прямую Σ4. Точка K4 пересечения Σ4, l4 позволяет определить горизонтальную и фронтальную проекции точки K пересечения прямой l с плоскостью Σ.

Определение точки пересечения прямой и плоскости

На рис. 2.16 плоскость Σ задана треугольником АВС, прямая l – точками 2, 3. На плоскости построена фронталь f, которой перпендикулярна вспомогательная плоскость проекций П4. Точка K пересечения прямой и плоскости имеет проекцию K4, которая является точкой пересечения отрезков .

У п. 1.5.8 показаны три способа определения линии пересечения двух плоскостей (рис. 1.42 – 1.46), не связанные с преобразованиями комплексного чертежа.

Определение линии пересечения плоскостей

Для определения линии MN пересечения двух плоскостей Σ, Ω способом замены плоскостей проекций (рис. 2.17) вводится вспомогательная плоскость П4, перпендикулярная плоскости Σ, на которую последняя проецируется в прямую Σ4. Прямая M4N4 пересечения Σ4, Ω4 позволяет определить горизонтальную и фронтальную проекции линии пересечения данных плоскостей .

На рис. 2.17 плоскости Σ, Ω заданы треугольниками АВС, DEF. В первом проведена фронталь f, которой перпендикулярна вспомогательная плоскость проекций П4. Линия пересечения плоскостей АВС, DEF имеет проекцию М4N4, принадлежащую проекции А4В4С4.

Способ вращения вокруг проецирующей оси

Метод вращения вокруг проецирующих осей этот метод заключается в том, что геометрический объект (прямую или плоскость) вращают вокруг проецирующей оси i до положения параллельности какой-либо плоскости проекций. В результате вращения геометрический объект проецируется на плоскость проекций в натуральную величину.

Вращение точки вокруг проецирующей оси

Способ вращения вокруг проецирующей оси — это один из способов преобразования комплексного чертежа, в котором геометрический объект вращается вокруг проецирующей оси до тех пор, пока не займет особое положение (рис. 2.18).

Поскольку любой геометрический объект является совокупностью точек в пространстве, для его вращения вокруг оси необходимо уметь вращать каждую точку.

На рис. 2.19 показан комплексный чертёж точки А до и после вращения вокруг осей i, j соответственно на углы α, β.

Вращение вокруг проецирующей оси

Реализация способа вращения вокруг проецирующей оси

Для вращения точки А вокруг проецирующей оси необходимо знать:

а) ось вращения– прямая линия, которая не изменяет своего положения в пространстве во время вращательного движения точки;

б) центр вращения – точка на оси вращения, для которого выполняется условие перпендикулярности отрезку оси вращения;

в) радиус вращения r – расстояние от центра вращения до точки А;

г) направление вращения;

Траекторией точки А при её вращении вокруг проецирующей оси является дуга окружности, принадлежащей плоскости уровня. Проекция траектории на одну из плоскостей проекций является дугой окружности, на две другие – прямой, параллельной соответствующим осям координат (рис. 2.19).

Способом вращении вокруг проецирующей оси можно определить :

а) натуральную величину отрезка (см. п. 2.2.2);

б) расстояния между геометрическими объектами (см. пп. 2.2.3 – 2.2.5);

в) точку пересечения прямой и плоскости (см. п. 2.2.6);

г) линию пересечения двух плоскостей (см. п. 2.3.5);

д) точки пересечения прямой линии с поверхностью тела вращения (см. п. 4.2.2.3).

Длина отрезка

Задача по определению натуральной величины отрезка имеет простейший способ реализации с использованием способа вращения вокруг проецирующей оси .

На рис. 2.20 приведён пример определения длины отрезка АВ общего положения. Через точку А проведена фронтально-проецирующая ось j, вокруг которой данный отрезок вращается до положения горизонтального уровня (фронтальная проекция параллельная оси х). Горизонтальная проекция является натуральной величиной отрезка АВ

Определение длины отрезка

Расстояние от точки до прямой и плоскости

Для определения расстояния от точки А до прямой l общего положения способом вращения вокруг проецирующей оси необходимо повернуть прямую до положения уровня.

На рис. 2.21 прямая l задана отрезком ВС. Фронтально-проецирующая ось вращения j проходит через точку В. Точки А, С вращаются вокруг оси на одинаковый угол. После вращения отрезок ВС занимает горизонтальное положение уровня По теореме о проецировании прямого угла (см. п. 1.4.8, рис. 1.26) горизонтальная проекция перпендикуляра, проведенного из точки к отрезку , проецируется на П1 в натуральную величину. Натуральная величина отрезка АN определяется путём вращения отрезка вокруг фронтально-проецирующей оси и равна длине отрезка

Определение расстояния от точки до прямой

Определение расстояния от точки до плоскости

Для определения расстояния от точки D до плоскости Σ общего положения способом вращении вокруг проецирующей оси необходимо повернуть плоскость в проецирующее положение.

На рис. 2.22 плоскость Σ задана треугольником АВС. Плоскости принадлежит фронталь f, проведенная через точки В, 1. Фронтально-проецирующая ось вращения j проходит через точку В. Точки А, С, D вращаются вокруг оси j на одинаковый угол. После вращения прямая f занимает горизонтально-проецирующее положение, а треугольник проецируется на П1 в отрезок прямой. Длина перпендикуляра , проведенного к плоскости , равна расстоянию от точки D к плоскости Σ.

Расстояние между параллельными прямыми, прямой и плоскостью, двумя плоскостями

Для определения расстояния между параллельными прямыми l, m способом вращения вокруг проецирующей оси прямые l, m вращаются вокруг этой оси до положения уровня.

На рис. 2.23 прямые заданные отрезками АВ, CD. Прямые вращаются вокруг фронтально-проецирующей оси j, яка проходить через точку А, до горизонтального положения уровня. На горизонтальной плоскости проекций П1 проекция перпендикуляра к образует прямые углы с проекциями . Расстояние между параллельными прямыми равно длине отрезка и определяется способом вращения вокруг проецирующей оси (равно длине отрезка

Для определения расстояния между параллельными прямой l и плоскостью Σ способом вращения вокруг проецирующей оси плоскость Σ вращается вокруг проецирующей оси до проецирующего положения.

Определение расстояния между параллельными прямыми

Определение расстояния между параллельными прямой и плоскостью

На рис. 2.24 плоскость Σ задана треугольником АВС, прямая l – отрезком DE. Фронталь f плоскости АВС, задана двумя точками В, 1, после вращения вокруг проецирующей оси j, проходящей через точку В, проецируется на плоскость П1 в точку у . Проекция треугольника является отрезком прямой. Расстояние от прямой l до плоскости АВС равно длине отрезка

Для определения расстояния между параллельными плоскостями Σ, Ω последние вращаются вокруг проецирующей оси до проецирующего положения.

На рис. 2.25 плоскости Σ, Ω заданы треугольниками АВС, DEF. Фронталь f плоскости АВС задана двумя точками В, 1. После вращения вокруг проецирующей оси j, проходящей через точку В, фронталь f проецируется на плоскость П1 в точку . Проекции треугольников являются отрезками прямых. Расстояние между данными плоскостями равно длине перпендикуляра

Определение расстояния между параллельными плоскостями

Расстояние между скрещивающимися прямыми

Для определения расстояния между скрещивающимися прямыми l, m применяется способ вспомогательной параллельной плоскости (см. п. 1.6.2, рис. 1.65 – 1.66), для чего вводится плоскость Σ, проходящая через прямую параллельно прямой l. После вращения вокруг проецирующей оси плоскость Σ проецируется в прямую линию. Расстояние между этой линией и соответствующей проекцией прямой l равен расстоянию между скрещивающимися прямыми.

Определение расстояния между скрещивающимися прямыми

На рис. 2.26 прямые l, m заданы отрезками АВ, CD. Вспомогательная плоскость Σ, задана треугольником CDE, параллельна отрезку АВ. После вращения вокруг горизонтально-проецирующей оси и, проходящая через точку D, треугольник CDE занимает фронтально-проецирующее положение . Длина перпендикуляра равна расстоянию между прямыми l, m.

Пересечение прямой и плоскости

Для определения точки K пересечения прямой l и плоскости Σ последняя вращается вокруг проецирующей оси до проецирующего положения. На рис. 2.27 плоскость задана треугольником АВС, прямая – отрезком DE. В плоскости построена фронталь f, которая после вращения вокруг фронтально-проецирующей оси j переводится в горизонтально-проецирующую прямую f . При этом плоскость проецируется в прямую , пересекающую проекцию в точке . Вращение этой точки вокруг оси j в обратном направлении позволяет определить искомые проекции K1, K2.

Определение точки пересечения прямой и плоскости

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение.

Плоскопараллельное перемещение тела

Плоскопараллельным движением тела называется такое его движение, в котором все точки тела имеют траектории, принадлежащие плоскостям, параллельным некоторой неподвижной плоскости. Последней в начертательной геометрии выбирают одну из плоскостей проекций.

Плоскопараллельные перемещения

Способ плоскопараллельного перемещения каждой точки тела реализуется с помощью комбинации двух движений: поступательного движения проецирующей оси и вращения вокруг этой оси (рис. 2.28).Целью применения способа плоскопараллельного перемещения является переведение геометрических объектов из общего положения в особое.

Способ вращения вокруг проецирующей оси (см. п. 2.2) является частным случаем способа плоскопараллельного перемещения, в котором ось вращения неподвижна.

Реализация способа плоскопараллельного перемещения тела Ф на его комплексном чертеже приведена на рис. 2.29. Она аналогична вращению вокруг проецирующей оси, но имеет существенное преимущество: одну из проекций объекта (на рис. 2.29 – это фронтальная проекция) можно переносить на свободное поле комплексного чертежа.

Основное правило плоскопараллельного перемещения

При плоскопараллельном перемещении геометрического объекта расстояния между всеми парами его точек не изменяются.

На рис. 2.29 длины проекций отрезков одинаковы так же, как одинаковы длины проекций отрезков и т.д..

Правило определения видимости для способа плоскопараллельного перемещения

При плоскопараллельном перемещении геометрического объекта видимость его линий не изменяется на одной из плоскостей проекций.

На рис. 2.29 на фронтальной проекции отрезок ВD невидим, все другие – видимы. После плоскопараллельного перемещения тела видимость отрезков на фронтальной проекции не изменилась, на горизонтальной – изменилась для отрезков AD, CD.

Способом плоскопараллельного перемещения решаются все задачи, описанные в п. 2.2, а также и те, которые не целесообразно решать способом вращения вокруг проецирующей оси.

Реализация способа плоскопараллельного перемещения

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми определяется такими способами:

а) вспомогательной параллельной плоскости (см. п. 1.6.2, рис. 1.65 – 1.66);

б) замены плоскостей проекций (п. 2.1.5, рис. 2.9);

в) вращения вокруг проецирующей оси (п. 2.2.5, рис. 2.26);

г) плоскопараллельного перемещения.

Способом параллельного перемещения можно определить расстояние между скрещивающимися прямыми l, m путём проецирования одной из прямых в точку.

На рис. 2.30 прямые l, m заданы отрезками АВ, CD. Их перемещение, параллельное плоскости П2, дозволяет перевести прямую l в горизонтальное положение уровня (проекция параллельна оси х; длина проекции является натуральной величиной отрезка АВ). Перемещение отрезков , параллельное плоскости П1, позволяет спроецировать прямую во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой). Расстояние между скрещивающимися прямыми l, m равно длине проекции перпендикуляра .

Определение расстояния между скрещивающимися прямыми

Угол между прямыми, прямой и плоскостью, двумя плоскостями

Для определения угла χ между двумя прямыми l, m, пересекающимися в точке K, способом плоскопараллельного перемещения необходимо перевести плоскость Σ,образованную этими прямыми , сначала в проецирующее положение, а потом – в положение уровня.

На рис. 2.31 прямые l, m заданы отрезками АВ, CD. В плоскости Σ, заданной прямыми l, m, вводится горизонталь h, которая с помощью перемещения, параллельного П1, переводится во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой; проекция является прямой линией). Перемещение плоскости параллельно плоскости П2 позволяет спроецировать угол χ между прямыми l, m в натуральную величину.

Определение плоского угла

Угол φ между прямой l и плоскостью Σ и между двумя плоскостями определяется с помощью перемещения плоскости Σ параллельно одной из плоскостей проекций до проецирующего положения.

На рис. 2.32 плоскость Σ задана треугольником АВС, прямая l – отрезком DE. В плоскости Σ проведена горизонтальная прямая уровня h, которая после плоскопараллельного перемещения проецируется в точку , а треугольник – на отрезок прямой. Угол φ между фронтальными проекциями равен искомому углу φ между прямой l и плоскостью Σ.

Определение угла между прямой и плоскостью

На рис. 2.33 плоскости Σ, Ω заданы треугольниками АВС, ABD. С помощью перемещения отрезка АВ (основы двугранного угла) параллельно П2, данный отрезок проецируется на П1 в натуральную величину. Перемещение отрезка параллельно П1 позволяет спроецировать заданные плоскости в прямые линии, пересекающиеся в точке, и определить угол θ между ними. Этот угол равен искомому двугранному углу при ребре АВ.

Определение двугранного угла

Натуральная величина плоской фигуры

Для определения натуральной величины плоской фигуры Ф способом плоскопараллельного перемещения необходимо перевести эту фигуру в положение уровня, перед этим спроецировав её на отрезок прямой линии.

На рис. 2.34 фигура Ф является треугольником АВС. В нём вводится горизонталь h, которая с помощью перемещения, параллельного П1, переводится во фронтально-проецирующее положение (проекция перпендикулярна оси х; проекция является точкой; проекция является отрезком прямой). Перемещение фигуры параллельно плоскости П2 позволяет определить натуральную величину треугольника АВС.

Определение натуральной величины плоской фигуры

Пересечение плоскостей

Для определения линии k (отрезка MN) пересечения двух плоскостей Σ, Ω способом плоскопараллельного перемещения одна из плоскостей переводится в проецирующее положение.

На рис. 2.35 плоскости заданы треугольниками АВС, DEF. В первом проведена горизонталь h, которая перемещается параллельно П1 до фронтально-проецирующего положения (проекция перпендикулярна оси х; проекция является точкой). При этом треугольник проецируется на отрезок который совпадает с проекцией линии пересечения, заданной точками . Искомые горизонтальная и фронтальная проекции отрезка MN определяются по линиям проекционной связи.

Определение линии пересечения плоскостей

Способ вращения вокруг линии уровня

При применении метода поворота плоскость проекции не изменяется, и изменяется исходное положение в пространстве. Изменение исходного положения осуществляется вращением Он вокруг оси. Линия проекции уровня или прямая линия обычно выбирается в качестве оси вращения.

Вращение точки вокруг линии уровня

Способ вращения вокруг линии уровня является одним из способов преобразования комплексного чертежа, в котором геометрический объект вращается вокруг линии уровня до тех пор, пока не займет особое положение (рис. 2.36).

На рис. 2.37 а показаны положения точки В до и после вращения вокруг горизонтальной прямой уровня.

Вращение вокруг линии уровня

Реализация способа вращения вокруг линии уровня

Для вращения точки В вокруг прямой уровня необходимо знать:

а) ось вращения – горизонталь, фронталь или профильная прямая уровня;

б) центр вращения – точка на оси вращения, для которой выполняется условие перпендикулярности отрезка оси вращения;

в) радиус вращения r – расстояние от центра вращения до точки В;

г) направление вращения.

Траекторией точки В при её вращении вокруг линии уровня является окружность, принадлежащая проецирующей плоскости. Проекция траектории на одну из плоскостей проекций является отрезком, перпендикулярным соответствующей проекции линии уровня (рис. 2.37 б).

На рис. 2.37 отрезок общего положения вращается вокруг горизонтали h до положения горизонтального уровня. Из горизонтальной проекции точки В проведена проекция r1 радиуса вращения, перпендикулярная оси h. На горизонтальной плоскости проекций прямой угол с основой проецируется в натуральную величину (по теореме о проецировании прямого угла, см. п. 1.4.8). Точка является центром вращения точки В. С помощью линии проекционной связи определяются фронтальные проекции центра вращения и радиуса вращения. С помощью способа вращения вокруг фронтально-проецирующей оси определяется натуральная величина радиуса вращения r (отрезок ), равная длине отрезка . Новое положение точки В (после вращения вокруг горизонтали h) удалено от центра вращения на величину радиуса вращения.

Способом вращения вокруг линии уровня целесообразно решать задачу на нахождение натуральной величины плоской фигуры и плоского угла – угла между двумя прямыми, пересекающимися в точке.

Натуральная величина плоской фигуры и плоского угла

Для определения натуральной величины плоской фигуры Ф необходимо повернуть её вокруг линии уровня до положения уровня.

На рис. 2.38 задан треугольник АВС. Определение его натуральной величины реализуется с помощью вращения вокруг горизонтали h, проходящей через его точки Из горизонтальной проекции точки В проведена проекция r1 радиуса вращения, перпендикулярная оси h. На горизонтальной плоскости проекций прямой угол с основой проецируется в натуральную величину. Точка является центром вращения точки В. С помощью линии проекционной связи определяются фронтальные проекции центра и радиуса вращения. С помощью способа вращения вокруг фронтально-проецирующей оси определяется натуральная величина отрезка , равная длине отрезка . Положение точки В (после вокруг горизонтали h) удалено от центра вращения на величину радиуса вращения r. Поскольку точки А, 1 принадлежат оси вращения, они остаются неподвижными. Точка является точкой пересечения лучей (точка является центром вращения точки С; отрезок перпендикулярен h1).

Определение натуральной величины плоской фигуры

На рис. 2.38 показана натуральная величина плоского угла χ при вершине А.

Способ совмещения

Способ совмещения является частным случаем способа вращения вокруг линии уровня. Осью вращения в нём является след плоскости, которой принадлежит плоская фигура.

Способ совмещения используется для нахождения натуральной величины плоской фигуры. В результате вращения последняя совмещается с одной из плоскостей проекций (рис. 2.39 а).

На рис. 2.39 б показана реализация способа совмещения плоскости Σ общего положения с горизонтальной плоскостью проекций П1. На фронтальном следе произвольно выбрана точка . Горизонтальная проекция точки 1 принадлежит оси х. Высота точки 1 равна . Центром вращения точки 1 вокруг горизонтального следа вращения плоскости Σ является точка . Натуральная величина r радиуса вращения равна длине отрезка 1. Величина радиуса вращения откладывается вдоль направления вращения Через точки строится новое положение фронтального следа. Таким образом, после вращения вокруг горизонтального следа плоскость Σ совмещается с горизонтальной плоскостью проекций П1.

Способ совмещения

На рис. 2.40 определена натуральная величина четырехугольника АВСD, принадлежащего плоскости Σ, заданной горизонтальным и фронтальным следами . Точки А, В, С, D вращаются вокруг горизонтального следа Для определения нового положения из точки А проводится горизонталь h и определяются точки Точка принадлежит новому положению горизонтали. Аналогично определяются точки . После вращения натуральная величина четырехугольника принадлежит плоскости проекций П1.

Определение натуральной величины плоской фигуры способом совмещения

Способ косоугольного проецирования

Изображения предметов на чертежах получают проецированием. Проецирование – это процесс получения изображения предмета на какой-либо поверхности . Получившееся при этом изображение называют проекцией предмета. Слово «проекция» в переводе с латинского означает «бросание вперед, вдаль».

Косоугольное проецирование на ортогональные плоскости проекций

Косоугольное проецирование — один из видов параллельного проецирования (см. п. 1.1.2.1, рис. 1.3), в котором проецирующие лучи не перпендикулярны плоскостям проекций П1, П2, П3.

Косоугольное проецирование задаётся направлением проецирования і, которое в общем случае направлено вдоль линии общего положения.

В начертательной геометрии используются три вида косоугольного проецирования:

а) на ортогональные плоскости проекций П1, П2, П3;

б) на плоскость особого положения (см. п. 2.5.2);

в) на биссекторную плоскость (см. п. 2.5.3).

Использование косоугольного проецирования направлено на искажение изображения геометрического объекта с целью упрощения его формы (прямая проецируется в точку, плоскость – в прямую и т.д.).

Правило косоугольного проецирования точки на ортогональные плоскости проекций

При косоугольном проецировании точки А на одну из плоскостей проекций П1, П2, П3 косоугольная проекция совпадает с соответствующим следом (см. п. 1.4.3, рис. 1.12) проецирующего луча і (рис. 2.41 а). Горизонтальная проекция точки принадлежит оси х, фронтальная – совпадает с косоугольной проекцией . Линии косоугольного проецирования параллельны соответствующим проекциям проецирующего луча і.

На рис. 2.41 б построен комплексный чертёж точки А и её косоугольной проекции А на фронтальную плоскость проекций П2.

Косоугольное проецирование на плоскость проекций

Способ косоугольного проецирования позволяет относительно быстро решать позиционные задачи на пересечение геометрических объектов (прямой и плоскости, двух плоскостей и т.д.).

На рис. 2.42 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введен проецирующий луч і, параллельный заданной плоскости. Косоугольная проекция плоскости Σ на плоскость проекций П2 (прямая ) является фронтальным следом плоскости Σ и пересекается с косоугольной проекцией в точке . С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.42 с целью упрощения горизонтальные проекции плоскости и прямой не обозначены (они совпадают с осью х). Их фронтальные проекции совпадают с косоугольными проекциями, поэтому нижний индекс «2» также не обозначен.

На рис. 2.43 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введен проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 (пряма ) является фронтальным следом плоскости Σ и пересекается с косоугольной проекцией по прямой , заданной отрезком . С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линий пересечения плоскостей

Косоугольное проецирование на плоскость особого положения

При косоугольном проецировании на плоскость особого положения (плоскость уровня или проецирующую плоскость) вводится вспомогательная плоскость с помощью одного из своих следов .

На рис. 2.44 а показан способ косоугольного проецирования на горизонтально-проецирующую плоскость . На рис. 2.44 б построен комплексный чертёж точки А, косоугольно спроецированной на эту плоскость. Горизонтальная проекция является точкой пересечения оси с горизонтальной проекцией проецирующего луча. Фронтальная проекция является точкой пересечения фронтальной проекции проецирующего луча с вертикальной линией проекционной связи, проведенной из точки .

Косоугольное проецирование на проецирующую плоскость

На рис. 2.45 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введены горизонтально-проецирующая плоскость и проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 является прямой пересекающейся с косоугольной проекцией в точке С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.45 для упрощения горизонтальные проекции плоскости и прямой не обозначены (они совпадают с осью ). Их фронтальные проекции не совпадают с проекциями на плоскость поэтому нижний индекс «2» обязателен.

На рис. 2.46 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введены горизонтально проецирующая плоскость и проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на плоскость проекций П2 пересекается с косоугольной проекцией плоскости Ω по прямой заданной отрезком С помощью линий проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линии пересечения плоскостей

Косоугольное проецирование на биссекторную плоскость

Биссекторная плоскость – это плоскость, равнонаклонённая к двум плоскостям проекций. При решении позиционных задач на пересечение геометрических объектов используются способы косоугольного проецирования, в том числе на биссекторную плоскость которая проходит через ось х, принадлежит ІІ и ІV четвертям (см. п. 1.3.1, рис. 1.6) и наклонена к плоскостям проекций П1, П2 под углом 45° (рис. 2.47 а).

Биссекторная плоскость

Основное свойство точек биссекторной плоскости

Любая точка А биссекторной плоскости имеет одинаковые по модулю и противоположные по знаку высоту z и глубину у (рис. 2.47).

На рис. 2.47 б построен комплексный чертёж точки А и её косоугольной проекции на биссекторную плоскость

Согласно основному свойству биссекторной плоскости на комплексном чертеже вместо обозначения косоугольных проекций которые совпадают , упрощенно обозначается только (рис. 2.48).

Косоугольное проецирование точки на биссекторную плоскость

Правило определения косоугольной проекции точки на биссекторную плоскость

Косоугольная проекция точки А на биссекторную плоскость является точкой пересечения горизонтальной и фронтальной проекций проецирующего луча і (рис. 2.48).

На рис. 2.49 построена точка K пересечения прямой l с плоскостью Σ, заданной параллельными прямыми а, b. Введен проецирующий луч і, параллельный заданной плоскости. Косоугольная проекция плоскости Σ на биссекторную плоскость П2 является прямой пересекающейся с косоугольной проекцией в точке С помощью линий проекционной связи точки на биссекторную плоскость определяются фронтальная и горизонтальная проекции точки K.

Определение точки пересечения прямой и плоскости

На рис. 2.50 построена линия k пересечения плоскости Σ, заданной параллельными прямыми а, b, с плоскостью Ω, заданной треугольником АВС. Введен проецирующий луч і, параллельный плоскости Σ. Косоугольная проекция плоскости Σ на биссекторную плоскость является прямой пересекающейся с косоугольной проекцией плоскости Ω по прямой заданный отрезком С помощью линий косоугольной проекционной связи определяются фронтальная и горизонтальная проекции искомой прямой k.

Определение линий пересечения плоскостей

Комбинированные способы

Описанные в разделах 1, 2 способы позволяют решать большое количество позиционных и метрических задач начертательной геометрии. При этом одну задачу можно решать разными способами, которые отличаются сложностью реализации. Поэтому, прежде, чем решать ту или иную задачу, необходимо проанализировать и сравнить между собой разные способы по критерию их сложности. Субъективное мнение авторов по этому вопросу приведено в табл. 2.1.

Таблица 2.1- Способы решения задач начертательной геометрии

Из табл. 2.1 видим, что универсальным способом решения почти всех задач начертательной геометрии является способ замены плоскостей проекций.

При решении комплексных задач способ замены плоскостей проекций можно дополнять другими способами (например, вращение вокруг проецирующей оси і, плоскопараллельного перемещения и т.д.). Умение объединять разные способы свидетельствует о высоком уровне опытности будущего инженера .

На рис. 2.51 определена натуральная величина треугольника АВС с использованием комбинации двух способов – замены плоскостей проекций и плоскопараллельного перемещения. На рис. 2.52 комбинацией двух указанных способов определён двугранный угол θ при ребре АВ.

Определение натуральной величины плоской фигуры

Определение двугранного угла

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник