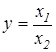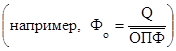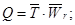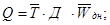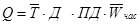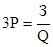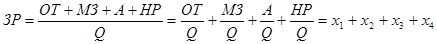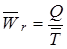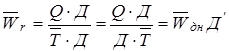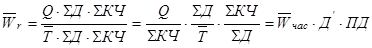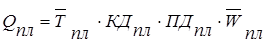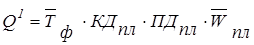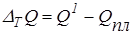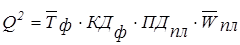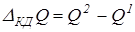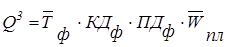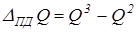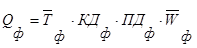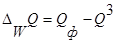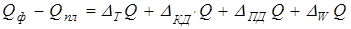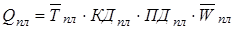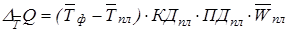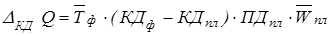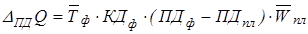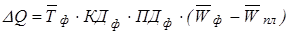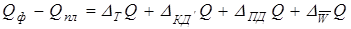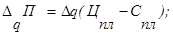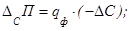Детерминированное моделирование факторных систем
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования факторных систем заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо выполнять ряд требований.
1. Факторы, включаемые в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показатели факторной модели должны быть количественно измеримыми, т. е. иметь единицу измерения и необходимую информационную обеспеченность.
4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, т. е. в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели. Используются, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели. Применяются, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели. Используются, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей.
Моделирование аддитивных факторных систем производится за счет расчленения одного или нескольких факторных показателей на составные элементы.
Моделирование мультипликативных факторных систем осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя на один и тот же показатель.
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.
Процесс моделирования факторных систем – очень сложный и ответственный в анализе хозяйственной деятельности. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Источник
Преобразование моделей
В экономическом анализе часто используются различные способы преобразования кратных детерминированных моделей:
§ формальное разложение модели;
1. Удлинение модели — это процедура разложения числителя на сумму отдельных факторов
.
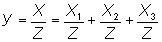
Например, себестоимость единицы продукции — это отношение суммарных затрат к объему продукции в натуральном выражении, и тогда модель имеет следующий вид:
,
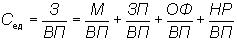
где Сед — себестоимость единицы продукции;
З — общая величина затрат;
ВП — выпуск продукции;
— материалоемкость продукции;
— зарплатоемкость;
— фондоемкость;
— уровень накладных расходов на единицу продукции.
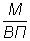
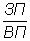
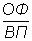
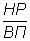
Полученная в результате процедуры удлинения новая модель имеет совершенно самостоятельные экономические показатели.
2. Способ формального разложения модели состоит в удлинении знаменателя исходной модели путем замены его на сумму или произведение отдельных факторов:
,
.
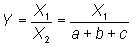
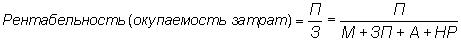
3. Расширение модели. Исходная модель расширяется за счет умножения числителя и знаменателя на один или несколько показателей, после чего полученная модель содержит набор новых факторов.
Например, если преобразовать формулу рентабельности активов, введя множитель РП / РП, то она примет следующий вид:
.
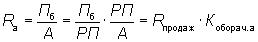
4. Способ сокращения модели состоит в создании новой модели путем деления числителя и знаменателя на один и тот же показатель Например, если числитель и знаменатель формулы фондорентабельности разделить на величину выручки от реализации, то новая модель будет иметь в числителе рентабельность продаж, а в знаменателе — фондоемкость продукции:
,
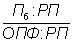
где Пб : РП — рентабельность продаж;
ОПФ : РП — фондоемкость продукции.
На практике для преобразования одной и той же модели могут использоваться различные способы, часто смешанные.
Источник
Способы моделирования и преобразования факторных систем
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.
Моделирование— это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения.В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделировании детерминированных факторных систем необходимо руководствоваться следующими правилами:
1. Факторы, включаемые в модель, и сами модели должны иметь явно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями, имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции.
В первой системе факторы находятся в причинной связи с результативным показателем, а во второй — в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая.
Все показатели факторной модели должны быть количественно измеримыми, т. е. должны иметь единицу измерения и необходимую информационную обеспеченность.
Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
Моделирование мультипликативных факторных системв АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители.
Например, при исследования процесса формирования объема производства продукции можно применять следующие модели:
ВП = ЧР х Д х ДВ;
ВП = ЧР х Д х П х ЧВ.
Моделирование аддитивных факторных систем осуществляется за счет расчленения одного или нескольких факторных показателей на составные элементы.
При использовании кратных моделей используют следующие способы преобразования :
Метод удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей.
Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей (данный способ широко применяется в экономическом анализе).
Метод сокращения представляет собой создание новой факторной модели путём деления числителя и знаменателя дроби на один и тот же показатель.
Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследования.
Процесс моделирования факторных систем − очень сложный и ответственный момент в экономическом анализе. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Источник
Способы преобразования функциональных факторных моделей
Мультипликативные модели
(например, 
)
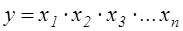
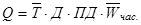
3. Кратные модели:
4. Смешанные (комбинированные) модели:
и т.д. 
, где:
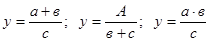
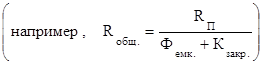
Rп – рентабельность продаж; Фемк. – фондоемкость; Кзакр. – коэффициент закрепления ОС.
Способы преобразования функциональных факторных моделей
а) в аддитивных моделях — за счет расчленения одного из факторных показателей на его составные элементы (слагаемые со знаком «+» либо «-»).
где Q — объем валовой продукции;
ВХП — объем внутрихозяйственного использования продукции.
б) в мультипликативных моделях — за счет последовательного расчленения факторов исходной системы на факторы — сомножители.
в) в кратных моделяхприменяют следующие способы их преобразования:
· Метод удлинения — удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. 
где х1 — зарплатоемкость продукции; х2 — материалоемкость продукции;
х3 — амортизацияемкость продукции; х4 – накладоемкость продукции.
· Способ формального разложения — удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей.
,
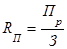
где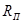 
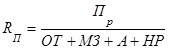
— рентабельность производства; Пр — сумма прибыли от реализации продукции; З — сумма затрат на производство и реализацию продукции,
.
· Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей.
где Q — валовая продукция предприятия;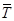 
— среднегодовая численность работников на предприятии.
где,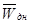 
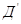
— среднедневная выработка;
— количество отработанных дней одним работником.
где,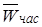 
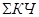
— среднечасовая выработка;
— количество отработанных часов всеми работниками;
ПД — продолжительность рабочего дня (в часах).
|
Способы детерминированного анализа:
|
индексный,
Элиминировать – устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Способ цепных подстановок заключается в составлении цепи последовательных расчетов, в которых каждый последующий расчет отличается от предыдущего заменой базового значения одного фактора на фактическое. Разница между результатами двух соседних расчетов отражает влияние на обобщающий показатель того фактора, значениями которого отличаются эти расчеты.
Последовательность имеет следующий вид:
Способ абсолютных разниц заключается в том, что для определения влияния одного фактора на обобщающий показатель необходимо разницу между фактической и базовой величиной этого фактора умножить на фактические величины факторов, стоящих в рабочей формуле до того фактора, влияние которого мы определяем, и на базовые величины факторов, стоящих после этого фактора.
Алгоритм расчета факторов способом абсолютных разниц в смешанных моделях типа Y = a · ( b – c ).
Прирост суммы прибыли за счет изменения объема реализации продукции:
;
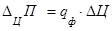
Имеются следующие данные о деятельности промышленного предприятия:
| № п/п | Показатель | Усл. обозн. | План | Факт | Отклонение | Выполн. плана, % |
| 1. | Среднегодовая численность рабочих, чел | Т | ||||
| 2. | Количество дней отработанных одним рабочим за год | КД¢ | ||||
| 3. | Средняя продолжительность рабочего дня, час | ПД | 7,8 | |||
 4. | Среднечасовая выработка, руб./час. | W | ||||
| 5. | Объем валовой продукции | Q |
1.Определить объем валовой продукции по плану и фактически, отклонение и процент выполнения плана.
2. Рассчитать требуемые аналитические данные.
3. Определить влияние факторов на выполнение плана по объему валовой продукции способом цепных подстановок.Сформулировать выводы.
1. Определяем, какие показатели являются количественными, какие – качественными.
2. Составляем модель факторной системы:
Q= Т ´ КД¢´ ПД ´ W
3. Определяем объем валовой продукции по плану и фактически:
Qпл = 5000 х 240 х 8 х 0,096 =
Qф = 5080 х 250 х 7,8 х 0,108 =
4. Определяем изменение результативного показателя по сравнению с планом:
5. Производим расчет влияния факторов на изменение результативного показателя:
а) за счет увеличения численности рабочих:
Q1 = Тф ´ КД¢ пл ´ ПДпл ´ Wпл = 5080 ´ 240 ´ 8 ´ 0,096 =
ΔTQ = Q1 – Qпл =
б) за счет увеличения количества рабочих дней, отработанных одним рабочим:
Q2 = Тф ´ КД¢ ф ´ ПДпл ´ Wпл = 5080 ´ 250 ´ 8 ´ 0,096 =
в) за счет сокращения продолжительности рабочего дня:
Q3 = Тф ´ КД¢ ф ´ ПДф ´ Wпл =
г) за счет повышения среднечасовой выработки:
ΔW Q = Qф – Q3 =
Используя балансовый метод как вспомогательный прием, проверим правильность решения задачи:
Баланс факторов: Qф – Qпл = ΔTQ + ΔКД Q + ΔПД Q + ΔW Q
Выводы: План по объему валовой продукции промышленного предприятия перевыполнен на 148248 тыс. руб., в том числе:
· за счет увеличения численности рабочих (на 80 человек) — на 14745,6 тыс. руб.;
· за счет увеличения количества отработанных дней одним рабочим за год (на 10 дней) — на 39014,4 тыс. руб.;
· сокращение продолжительности рабочего дня на 0,2 часа повлекло сокращение объема продукции на 24384 тыс. руб.;
Имеются следующие данные о деятельности авторемонтного предприятия:
| № п/п | Показатель | Усл. обозн. | Прош. год | Отчет. год | Отклон. | Выполн. пана,% |
| 1. | Выручка от реализации продукции (без НДС и акцизов), тыс. руб. | Q | 581,4 | 876,0 | ||
 2. | Среднегодовая стоимость основных производственных фондов, тыс. руб. | ОПФ | 323,0 | 365,0 | ||
| 3. | Фондоотдача, руб. | Фо |
1. Проанализировать эффективность использования основных производственных фондов в отчетном году по сравнению с прошлым.
2. Определить фондоотдачу за прошлый и отчетный год, отклонение и процент выполнения плана (записать в таблицу).
3. Рассчитать требуемые аналитические данные.
4. Определить влияние фондоотдачи и среднегодовой стоимости основных производственных фондов на изменение выручки от реализации продукции способом абсолютных разниц.Сформулировать выводы.
Решение задачи 2:
1. Определяем аналитические данные: отклонение и процент выполнения плана и записываем их в таблицу.
2. Определяем фондоотдачу основных производственных фондов за прошлый год:
Фо пг = Qпг / ОПФпг;
Фо пг = 581,4 / 323,0 =
Определяем фондоотдачу основных производственных фондов за отчетный год:
Фо ог = Qог / ОПФог;
Фо ог = 876,0 / 365,0 =
3. Определяем изменение фондоотдачи в отчетном году по сравнению с прошлым годом:
ΔФо = Фо ог – Фо пг =
4. Запишем рабочую формулу для анализа:
Q = ОПФ ´ Фо
5. Определяем влияние изменения факторов на изменение выручки от реализации продукции:
а) за счет увеличения среднегодовой стоимости основных производственных фондов:
 |
ΔОПФQ =(ОПФог –ОПФпг) ´ Фо пг =
б) за счет увеличения фондоотдачи:
ΔФоQ = ОПФог ´ (Фо ог – Фо пг) =
Вывод: В отчетном периоде по сравнению с плановым на авторемонтном предприятии отмечается повышение эффективности использования основных производственных фондов. Увеличение выручки от реализации продукции в отчетном периоде на 294,6 тыс. руб. достигнуто:
— за счет увеличения среднегодовой стоимости основных производственных фондов — на 75,6 тыс. руб.;
— за счет роста фондоотдачи – на 219 тыс. руб. (то есть преимущественно за счет интенсивного фактора).
Источник
