Способы преобразования комплексного чертежа задача

Способы преобразования комплексного чертежа

Назначение способов преобразования чертежа состоит в том, чтобы геометрическую фигуру общего положения расположить в частное положение относительно плоскостей проекций с целью использования свойств ее проекций.Например, преобразование плоскости общего положения в плоскость уровня позволит определить по соответствующей проекции ее натуральную величину.

Способы преобразования комплексного чертежа разделяют на две группы по признаку, определяющему положение фигуры и плоскостей проекций друг относительно друга или направление проецирования:

1. Изменяют положение плоскостей проекций или направление проецирования так, чтобы неподвижная в пространстве фигура оказалась в частном положении. К этой группе относят:

способ замены плоскостей проекций;

способ дополнительного проецирования.

2. Изменяют положение геометрической фигуры в пространстве так, чтобы она оказалась в частном положении относительно фиксированной системы плоскостей проекций. В эту группу включают:

способ плоскопараллельного перемещения;

Задачи, решаемые с помощью способов преобразования комплексного чертежа, сводятся к следующим основным задачам, в которых необходимо преобразовать:

прямую (плоскость, цилиндрическую или призматическую поверхности) в проецирующую фигуру;

прямую (плоскую линию или плоскость) в фигуру уровня.

Рассмотрим последовательно все способы преобразования, за исключением способа дополнительного проецирования, с которым рекомендуется ознакомиться самостоятельно по учебнику [1].

Способ замены плоскостей проекций

Сущность способа состоит в замене первоначальной системы взаимно перпендикулярных плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций при неизменном положении геометрической фигуры в пространстве.

Для решения конкретной задачи выполняют одно или два последовательных преобразования способом замены, например, Π₁Π₂→Π₁Π₄илиΠ₁Π₂→Π₁Π₄→Π₅Π₄. Во втором случае преобразование называют композицией преобразований. При каждом шаге в данном способе заменяется только одна плоскость проекций, а другая остается общей для двух систем.

Рассмотрим механизм и особенности способа замены плоскостей проекций на примере преобразования комплексного чертежа точки (рис. 28).

При замене, например, фронтальной плоскости проекций Π₂ новой вертикальной плоскостьюΠ₄горизонтальная плоскостьΠ₁ в данном случае является общей для двух систем плоскостей проекций, вследствие чего проекцияА₁точкиАна эту плоскость является также общей для этих систем. При этом сохраняется неизменной величина расстояния (АА₁) от заданной точки до этой плоскости проекций и, как следствие, равенство ее проекций на плоскостиΠ₂иΠ₄, т. е.АА₁ =А₂А₁₂ =А₄А₁₄, что позволяет выполнять на комплексном чертеже построение новой проекцииА₄заданной точки (см рис. 28).

Еще одна особенность способа замены плоскостей проекций заключается в том, что комплексный чертеж образуется совмещением плоскостей проекций с той плоскостью, которая является общей для двух систем. В рассматриваемом на рис. 28 примере такой плоскостью является горизонтальная плоскость проекций.

В качестве примера рассмотрим задачу преобразования прямой общего положения в проецирующую. Для достижения конечного результата необходимо провести замену двух плоскостей проекций, используя композицию преобразований, т. е. два последовательных преобразования (рис. 29).

Замена одной плоскости проекций, например, Π₂ наΠ₄позволяет преобразовать прямую общего положения только в прямую уровня, так как невозможно сразу расположить новую вертикальную плоскость проекцийΠ₄перпендикулярно заданной прямой. Далее, заменяя последовательно вторую плоскость проекцийΠ₁наΠ₅ и располагая ее перпендикулярно прямойАВ, получаем конечный результат (см. рис. 29).

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф. Ф.,

5.2. Задачи преобразований комплексного чертежа

Все метрические и позиционные задачи можно свести к одной из следующих четырех задач.

Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня (горизонталь или фронталь) новой системы.

Для решения задачи необходимо заменить плоскость проекций П₁, или П₂ новой плоскостью проекций П₄, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П₂ новой плоскостью П₄ 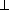П₁ и параллельной прямой АВ.

Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.1), необходимые для решения первой основной задачи на преобразование комплексного чертежа:

.

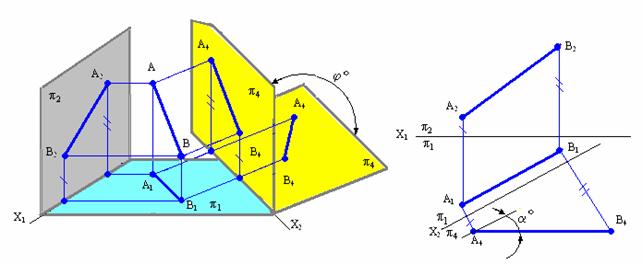
Рис. 5.1. Изображение преобразования прямой общего положения в прямую положения уровня: а — в пространстве; б – на комплексном чертеже

1) провести новую ось проекций х₁₄ параллельно А₁В₁ на произвольном расстоянии от нее; такое положение оси х₁₄ обусловливается тем, что П₄ параллельна АВ. В частном случае, если плоскость П₄ проведена непосредственно через прямую АВ, ось х₁₄ = А₁В₁;

3) построить проекции точек А и В на плоскости П₄.

Прямая А₄В₄ является проекцией прямой АВ на плоскость П₄. Прямая AB в новой системе плоскостей проекций П₁/П₄ является фронталью.
Отрезок [АВ] прямой проецируется на плоскость П₄ в истинную величину, т.е. | А₄В₄ | = | АB |, a- величина угла наклона прямой АВ к плоскости П₁.

3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей.

.

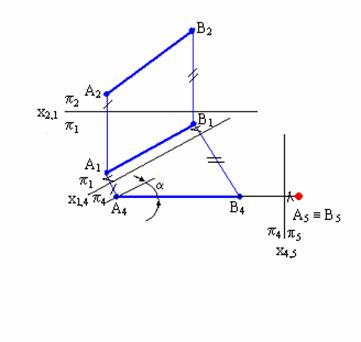
Рис. 5.2 Преобразование прямой АВ общего положения в горизонтально-проецирующую.

Для решения задачи заменить плоскость П₂ исходной системы П₂/П₁ плоскостью П₄ // А₁В₁, при этом плоскость П₄ будет перпендикулярной П₁ так как АВ // П₄ и образует с ней новую систему плоскостей проекций П₁/П₄.

Построения на комплексном чертеже:

1) провести новую ось проекций х₁₄ // А₁В₁;

2) построить проекции точек А и В на плоскости П₄, взяв координаты точек из плоскости П₂;

3) заменить плоскость П₁ на новую П₅, которая будет П₄ и А₄В₄. Для этого нужно провести новую ось проекций х_4,5.

Так как расстояния точек А и В до плоскости П₄ одинаковы, то проекции их на плоскости П₅ совпадут, А₅ ≡ В₅, прямая АВ (А₅В₅) в новой системе плоскостей проекций заняла проецирующее положение и стала горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П₅ перпендикулярная прямой, не будет перпендикулярна ни одной из «старых» плоскостей проекций, и, следовательно, не сможет образовать ни с одной из них прямоугольной системы плоскостей проекций.

Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Прямую общего положения следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую (рис. 5.2).

Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей (рис. 5.3).

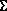
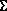
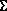
Для решения задачи необходимо заменить плоскость П₁ или П₂ исходной системы П₂/П₁ новой плоскостью П₄, перпендикулярной плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости , преобразовать в проецирующую, то плоскость в новой системе плоскостей проекций станет проецирующей.

Проще всего для этой цели воспользоваться линией уровня.

.

Рис. 5.3. Преобразование плоскости общего положения в проецирующую

На чертеже плоскость (АВС) преобразована во фронтально проецирующую (см. рис. 5.3) путем преобразования горизонтали h(h₁,h₂), принадлежащей плоскости , во фронтально- проецирующую прямую. В новой системе плоскостей проекций П₁/П₄ плоскость является фронтально проецирующей (4), и поэтому ее проекция на П₄ вырождается в прямую линию ₄ (С₄, А₄, В₄).

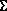
α – величина угла наклона плоскости 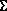к плоскости П₁.

Задача №4. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала плоскостью уровня (параллельной одной из плоскостей проекций) новой системы.

.

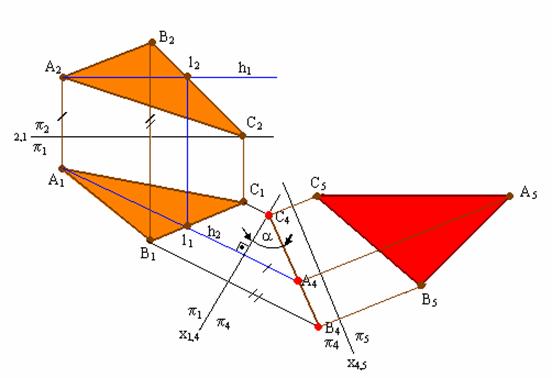
Рис. 5.4. Решение 4-й задачи на преобразование плоскости общего положения в плоскость уровня

Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П₄, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций.

Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3 на преобразование комплексного чертежа, а затем проецирующую плоскость преобразовать в плоскость уровня. На рис. 5.4 показано преобразование плоскости Δ(АВС) в горизонтальную плоскость уровня.

Допустим, что заданная плоскость Г является фронтально проецирующей (рис. 5.5). Заменим плоскость П₁ новой плоскостью проекций П₄, параллельной плоскости Г (ΔАВС) и, перпендикулярной незаменяемой плоскости П₂. В новой системе плоскостей проекций П₂/П₄ плоскость Г (АВС) станет горизонтальной плоскостью уровня.

.

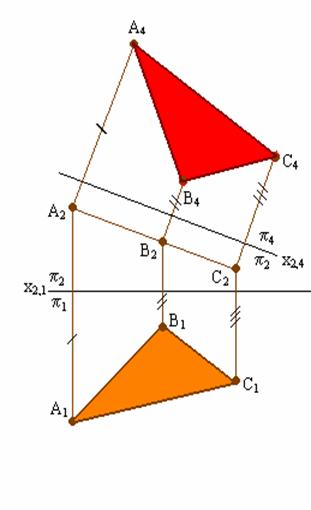
Рис. 5.5. Решение четвертой задачи на преобразование комплексного чертежа

Построения на комплексном чертеже:

1) проводим новую ось проекций х₂₄ параллельно А₂С₂ на произвольном от нее расстоянии; такое положение оси проекций х₂₄ обусловливается тем, что П₄ параллельна Г (АВС). Ось х₂₄ совпадает с прямой (А₂С₂), если плос- кость П₄ совмещается с плоскостью Г (АВС);

2) построим проекции точек А, В и С на плоскость П₄;

3) треугольник А₄В₄С₄ является проекцией треугольника АВС на плоскость П₄.

Примечание. Так как плоскость треугольника АВС параллельна П_4, значит отображение этого треугольника на П₄ будет в натуральную величину.

В данном конспекте лекций рассматривается только способ замены плоскостей проекций.

Вопросы для самоконтроля

1. Как нужно располагать дополнительные плоскости проекций, чтобы прямую общего положения преобразовать в: а) прямую уровня; б) проецирующую прямую.

2. Как нужно располагать дополнительные плоскости проекций, чтобы плоскость общего положения преобразовать в: а) проецирующую; б) плоскость уровня?

3. Какие основные метрические задачи можно решать с помощью дополнительного проецирования?

4. Какие метрические задачи относят к основным?

Источник

Четыре исходных задачи преобразования чертежа

В подавляющем большинстве метрических задач участвуют прямые и плоскости. Если будет известно заранее, какие построения необходимо выполнить, чтобы прямая (или плоскость) общего положения заняла частное положение, то это значительно облегчит решение многих метрических задач.

Частных положений прямой — два (прямая уровня и проецирующая прямая), частных положений плоскости — тоже два (плоскость уровня и проецирующая плоскость). Отсюда следует, что должны существовать четыре исход­ных задачи преобразования комплексного чертежа, в результате которых:

1. Прямая общего положения становится прямой уровня.

2. Прямая общего положения становится проецирующей прямой.

3. Плоскость общего положения становится проецирующей плоскостью.

4. Плоскость общего положения становится плоскостью уровня.

Для решения этих задач будем использовать метод замены плоскостей проекций, хотя каждая из них могла бы быть решена и методом вращения, и методом плоскопараллельного переноса.

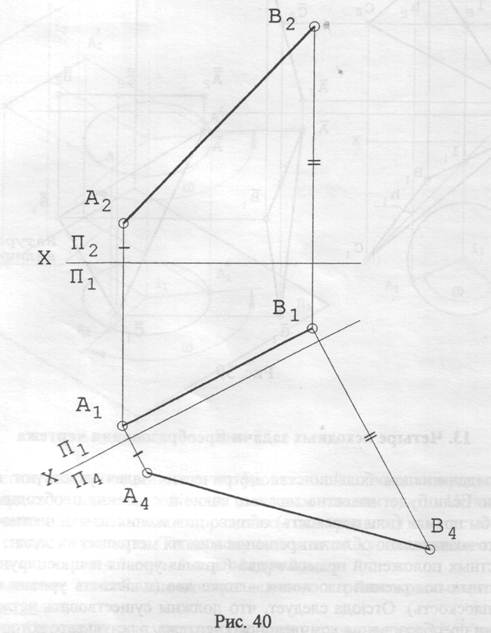
Задача 1.Преобразовать прямую общего положения АВ в прямую уровня (рис. 40).

Решение.Для решения этой задачи введем новую фронтальную плоскость проекций П₄, расположенную параллельно горизонтальной проекции А₁В₁ прямой АВ. Поскольку при введении новой фронтальной плоскости про­екций координаты Z точек А и В не должны измениться, дальнейшие построения ясны из чертежа. Отметим, что проекция А₄В₄ представляет собой натуральную величину отрезка АВ.

Другими словами, решение исходной задачи 1 преобразования ком­плексного чертежа представляет собой ещё один способ нахождения натуральной величины отрезка прямой общего положения.

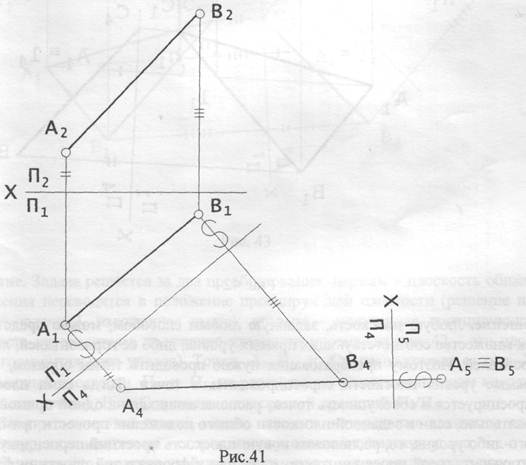
Задача2. Прямую общего положения преобразовать в положение проецирующей прямой (рис. 41).

Решение.Задача решается за два преобразования, поскольку здесь понадобится делать две замены плоскостей проекций: первой заменой прямая обще­го положения переводится в положение прямой уровня, а второй заменой полу­ченная прямая уровня переводится в проецирующую прямую. Первое преобра­зование — решение первой исходной задачи преобразования. Так как вводимая во втором преобразовании плоскость проекций П₅ — новая горизонтальная плоскость проекций, точка А₅ располагается на линии проекционной связи А₄А₅ на расстоянии, равном величине координаты У точки А в системе плоскостей проекций П₁/П₄.

Зная решение этой задачи, можно найти:

— расстояние между параллельными прямыми;

— расстояние между скрещивающимися прямыми;

— расстояние от точки до плоскости;

— натуральную величину двугранного угла (если линию пересечения двух плоскостей представить в виде проецирующей прямой).

Задача 3.Перевести плоскость общего положения, заданную треугольником АВС, в проецирующую плоскость (рис. 42).

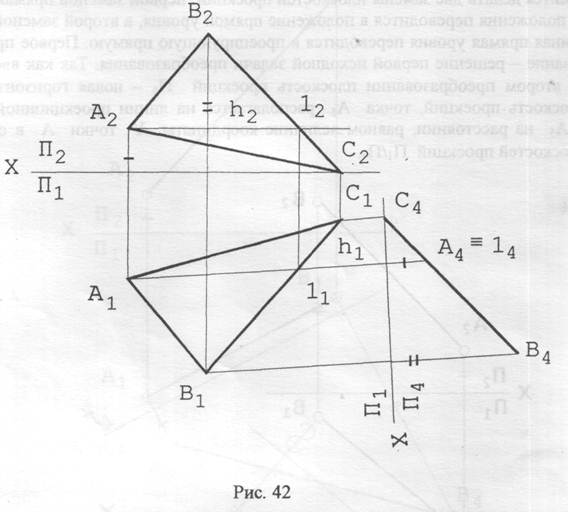Решение.Любую плоскость, заданную любым способом, можно представить как множество соответствующих прямых уровня, либо её горизонталей, либо ее фронталей. Поэтому преобразования нужно проводить таким образом, чтобы прямые уровня плоскости спроецировались в точки. Тогда сама плоскость спроецируется в совокупность точек, располагающихся на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно к горизонтальной проекции горизонтали или к фронтальной проекции фронтали, получим соответствующую проецирующую плоскость (рис. 42).

Зная решение этой задачи и поступая аналогично, можно находить:

— расстояние от точки до плоскости;

— расстояние между плоскостью и параллельной ей прямой;

— расстояние между параллельными плоскостями.

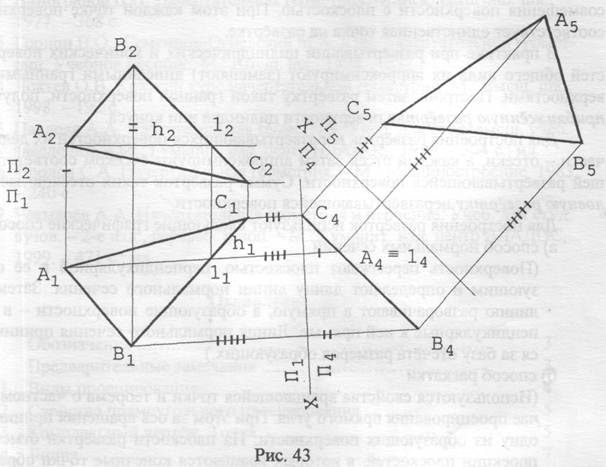
Задача 4.Плоскость общего положения, заданную треугольником АВС, перевести в положение плоскости уровня (рис. 43)

Решение.Задача решается за два преобразования: первым — плоскость общего положения переводится в положение проецирующей плоскости (решение исходной задачи 3, изложенное выше); вторым полученная проецирующая плоскость переводится в положение плоскости уровня (на рис. 42 — это плоскость горизонтального уровня). Точки А₅, В₅ и С₅ расположены от оси X, разделяющей плоскости П₄ и П₅ на расстояниях, равных величинам коорди­нат Y для точек А, В и С в системе плоскостей проекций П₁/П₄.

Зная решение этой задачи, можно находить натуральные величины плоских фигур, а следовательно — сторон многоугольников, плоских углов.

Заметим, что решение этой же задачи методом плоскопараллельного переноса приведено на рис. 39 в предыдущем разделе.

14. Развёртывание поверхностей

Развёртка поверхности — фигура, получающаяся после одностороннего совмещения поверхности с плоскостью. При этом каждой точке поверхности соответствует единственная точка на развёртке.

В практике при развёртывании цилиндрических и конических поверхностей общего вида их аппроксимируют (заменяют) вписанными гранными по­верхностями. Построив затем развёртку такой гранной поверхности, получают приближённую развёртку поверхности цилиндра или конуса.

Для построения развёрток неразвёртывающихся поверхностей их делят на части — отсеки, а каждый отсек затем аппроксимируют отсеком соответствующей развёртывающейся поверхности. Сумма развёрток таких отсеков даёт ус­ловную развёртку неразвёртывающейся поверхности.

Для построения развёрток используют следующие графические способы:

а) способ нормальных сечений

(Поверхность пересекают плоскостью, перпендикулярной к её образующим и определяют длину линии нормального сечения. Затем эту линию разворачивают в прямую, а образующие поверхности — в перпендикулярные к ней прямые. Линия нормального сечения принимает­ся за базу отсчёта размеров образующих.)

б) способ раскатки

(Используются свойства вращающейся точки и теорема о частном случае проецирования прямого угла При этом за ось вращения принимают одну из образующих поверхности. На плоскости развёртки отмечают проекции плоскостей, в которых вращаются конечные точки образую­щих поверхности. Зная расстояния между конечными точками, на плоскости развёртки находят эти точки и сами образующие.)

в) способ триангуляции

(Развёртываемая поверхность аппроксимируется многогранной поверхностью с треугольными гранями. Определяют размеры сторон ка­ждой грани. Общая развёртка представляет собой сумму развёрток треугольников-граней.)

Более подробное описание каждого из этих методов можно найти в литературе.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник