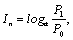Способы преобразования информации формы представления информации передача информации

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

1.1. Информатика как наука. Понятие информации

Информатика — это наука о способах и методах представления, обработки, передачи и хранения информации с помощью ЭВМ.

Термин «информатика» происходит от французского Informaticue. В англоязычной литературе можно встретить другой термин, обозначающий ту же отрасль человеческой деятельности,- Computer Science.

Четкого определения термина «информация» не существует; есть множество вариантов, приведем некоторые из них.

Определение 1. Информация есть форма движения материи.

Определение 2. Информация — одна из трех составляющих основ мироздания наряду с материей и энергией.

Определение 3. Информация есть отражение реального мира, это сведения, которые один реальный объект содержит о другом реальном объекте.

Согласно последнему определению, понятие информации связывается с определенным объектом, свойства которого она отражает.

Информация о любом материальном объекте может быть получена путем наблюдения за этим объектом, вычислительного эксперимента над ним или путем логического вывода. В связи с этим информацию делят на доопытную, или априорную, и послеопытную, или апостериорную, полученную в результате проведенного эксперимента.

Информация передается с помощью сообщений. Под сообщением будем понимать различные средства общения людей.

Соответствие между сообщением и информацией не является взаимно однозначным. Для одной и той же информации могут существовать различные передающие ее сообщения, которые появляются при добавлении сообщения, не несущего никакой дополнительной информации. Сообщения, передающие одну и ту же информацию, образуют класс эквивалентных сообщений.

В то же время одно и то же сообщение может передавать совершенно различную информацию.

Таким образом, одно и то же сообщение, по-разному интерпретированное, может передавать разную информацию. Правило интерпретации может быть известно лишь ограниченному кругу лиц; существуют правила интерпретации для специальных языков.

Связь между сообщением и информацией особенно отчетлива в криптографии: никто посторонний не должен суметь извлечь информацию из передаваемого сообщения, иначе это означало бы, что он располагает «ключом».

В житейском смысле под информацией мы понимаем совокупность интересующих нас сведений, знаний, набор данных и т. д. Информация не может существовать без наличия источника и потребителя информации. Основной источник и потребитель информации — это человек, поэтому можно сказать, что существует столько видов информации, сколько органов чувств у человека.

Информацию можно отнести к абстрактным понятиям. Однако ряд ее особенностей приближает информацию к материальному миру. Информацию можно получить, записать, передать, продать, купить, своровать, уничтожить, в конце концов, информация может устареть.

1.2. Методы оценки и виды информации

При оценке информации различают три аспекта: синтаксический, семантический и прагматический.

Синтаксический аспект связан со способом представления информации вне зависимости от ее смысловых и потребительских качеств и рассматривает формы представления информации для ее передачи и хранения (в виде знаков и символов). Данный аспект необходим для измерения информации. Информацию, рассмотренную только в синтаксическом аспекте, называют данными.

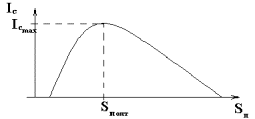
Семантический аспект передает смысловое содержание информации и соотносит ее с ранее имевшейся информацией.

S_п — тезаурусная мера получателя;
I_c — семантическое количество информации.

Прагматический аспект передает возможность достижения цели с учетом полученной информации.

где P₀ — вероятность достижения цели до получения информации; P₁ — вероятность достижения цели после получения информации; I_п — прагматическое количество информации; а > 1.

1. Научная информация (наиболее полно отражает объективные закономерности природы, общества и мышления);

2. Информация управления:

а) производственная, связанная с управлением людьми;

б) техническая, связанная с управлением техническими объектами.

Также классификация информации может производиться по следующим основаниям:

1. По областям применения:

2. По назначению:

1.3. Методы хранения и передачи информации

Хранение и передача информации осуществляются за счет преобразования информации в удобную форму в зависимости от условий, в которых находятся источник и потребитель информации. Передача информации может осуществляться напрямую, а также за счет усиления сигнала (рупор, локальная компьютерная сеть, письменная речь и т. д.) или же путем преобразования сигнала и передачи его на далекие расстояния (телефон, телеграф, радио, телевидение, глобальные компьютерные сети и т. д.).

Хранение информации осуществляется на долговременных носителях: камень, пергамент, кожа, бумага, магнитные носители, лазерные диски, серверы вычислительных сетей и т. п. При этом передача освобождается от гнета реального времени, становятся возможными даже сообщения человека самому себе (заметки на память). Таким образом за счет использования «инструмента» уменьшается нагрузка на человеческую память. В настоящее время основным средством хранения информации является персональный компьютер (ПК) и другие средства вычислительной техники.

Процедура хранения информации в ПК состоит в том, чтобы сформировать и поддерживать структуру хранения данных в памяти компьютера. Современные структуры хранения данных должны быть независимы от программ, использующих эти данные, и реализовывать принципы полноты и минимальной избыточности. Такие структуры получили название «базы данных». Процедуры создания структуры хранения (базы данных), актуализации, извлечения и удаления данных производятся при помощи специальных программ, называемых «системы управления базами данных».

Процедура актуализации данных позволяет изменить значения данных, записанных в базе, либо дополнить определенный раздел, группу данных. Устаревшие данные могут быть удалены с помощью соответствующей операции.

Процедура извлечения данных необходима для пересылки из базы данных необходимых сведений либо для преобразования, либо для отображения, либо для передачи по вычислительной сети.

Хранение и передача данных тесно связаны между собой, для выполнения этих процедур используют сетевые информационные технологии. Программы, предназначенные только для хранения и передачи данных, носят название «информационные хранилища» и представляют собой компьютеризированные архивы.

1.4. Обработка информации. Двоичная система счисления

Источниками и носителями информации могут быть сигналы любой природы: речь, музыка, текст, показания приборов и т. д. Однако хранение, передача и переработка информации в ее естественном физическом виде большей частью неудобна, а иногда и просто невозможна. В таких случаях применяется кодирование.

Кодирование — это процесс установления взаимно однозначного соответствия элементам и словам одного алфавита элементов и слов другого алфавита.

Кодом называется правило, по которому сопоставляются различные алфавиты и слова.

Всю информацию, участвующую в электронном вычислительном процессе, можно разделить на обрабатываемую (данные) и управляющую (программы).

В схеме преобразования информации в данные (рис. 1) представлены проводимые над информацией и данными процессы, которые образуются после введения информации в компьютер. Также представлены процедуры и связи между ними, с помощью которых осуществляются эти процессы.

Процедура отображения — преобразование информации в вид, удобный для восприятия человеком.

Практически всегда основой кодирования чисел в современной ЭВМ является двоичная система счисления.

Системой счисления называется способ записи чисел при помощи ограниченного числа символов (цифр).

Позиционной системой счисления называется система счисления, при которой число, связанное с цифрой, зависит от места, которое она занимает.

Рис. 1. Схема преобразования информации в данные и действий над ними

Пример. Перевести в десятичную запись число (10000111) ₂ . Перевести в двоичную запись число 89. Сложить в двоичной записи эти два числа, результат перевести в десятичную запись.
Решение:
(10000111) ₂ =1·2 7 + 1·2 2 + 1·2 1 + 1·2 0 = 128 + 4 + 2 + 1 = (135) 10 ,
(89) ₁₀ = 1·2 6 + 1·2 4 + 1·2 3 + 1·2 0 = (1011001) ₂ ,

10000111

+ 1011001

11100000,

1.5. Представление информации в компьютере

Единицы измерения информации

Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация для обработки на компьютере должна быть преобразована в числовую форму. Например, чтобы перевести в числовую форму музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме.

С помощью программ для компьютера можно выполнить преобразования полученной информации, например, наложить друг на друга звуки различных источников. После этого результат можно преобразовать обратно в звуковую форму.

Аналогичным образом на компьютере можно обработать и текстовую информацию. При вводе в компьютер каждая буква кодируется определенным числом, а при выводе на внешние устройства для восприятия человеком по этим числам строится соответствующее изображение буквы.

Бит — единица информации, представляющая собой двоичный разряд, который может принимать значение 0 или 1.

Байт — восемь последовательных битов. В одном байте можно кодировать значение одного символа из 256 возможных (256 = 28). Более крупными единицами информации являются следующие: 1 Кбайт = 210 = 1024 байта; 1 Мбайт = 220 байт = 1024 Кбайта; 1 Гбайт = 230 байта и т. д. В них обычно измеряется емкость запоминающих устройств.

Компьютеры представляют собой средства обработки и хранения информации. Для того чтобы информация превратилась в данные, ее надо собрать, соответствующим образом подготовить и только после этого ввести в ЭВМ, представив в виде данных на машинных носителях. На этапах подготовки и ввода информации осуществляется процедура контроля — выявление и устранение ошибок. Обычно для контроля применяют совокупность ручных и машинных методов, направленных на обнаружение ошибок. Методы подразделяются на визуальный (перед вводом в компьютер человек просматривает информацию на наличие возможных ошибок), логический (информация по мере ввода в компьютер сравнивается с эталоном, правилами или ранее имевшейся информацией) и арифметический (проверка путем подсчета контрольных сумм, применяется в бухгалтерии). Ввод информации осуществляется ручным способом с клавиатуры или с помощью сканера и программ распознавания. Программы распознавания делятся на программы оптического распознавания, распознающие печатный текст, и интеллектуального — для распознавания рукописного текста.

Вопросы

1. Какое количество информации содержит один разряд двоичного числа?

2. Как записать число (17) ₁₀ в двоичной системе счисления?

3. Какие этапы проходит информация, чтобы предстать в виде данных?

4. Для чего необходима процедура актуализации данных?

Источник

Теория алгоритмов и программ — Практика

3. Формы представления информации

Передача информации производится с помощью сигналов, а самим сигналом является изменение некоторой характеристики носителя с течением времени. При этом в зависимости от особенностей изменения этой характеристики (т.е. параметра сигнала) с течением времени выделяют два типа сигналов: непрерывные и дискретные .

Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала

Если обозначить Z- значение параметра сигнала, at- время, то зависимость Z(t) будет непрерывной функцией (рис.1.2,а).

Рис. 1.2. Непрерывные (а) и дискретные (б) сигналы

Примерами непрерывных сигналов являются речь и музыка, изображение, показание термометра (параметр сигнала — высота столба спирта или ртути — имеет непрерывный ряд значений) и пр.

Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.

Пример дискретных сигналов представлен на рис. 1.2,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров . Примерами устройств, использующих дискретные сигналы, являются часы (электронные и механические), цифровые измерительные приборы, книги, табло и пр.

Поскольку последовательность сигналов есть сообщение, качество прерывности-непрерывности сигналов переносится и на сообщение — существуют понятия «непрерывное сообщение» и «дискретное сообщение». Очевидно, что дискретным будет считаться сообщение, построенное из дискретных сигналов. Гораздо меньше оснований приписывать данное качество самой информации, поскольку информация — категория нематериальная и не может обладать свойством дискретности или непрерывности. С другой стороны, одна и та же информация, как уже было сказано, может быть представлена посредством различных сообщений, в том числе и отличающихся характером сигналов. Например, речь, которую слышим, можно записать в аналоговом виде с помощью магнитофона, а можно и законспектировать посредством дискретного набора букв. По этой причине в информатике существуют и используются сочетания «непрерывная информация» и «дискретная информация». Их нужно понимать только как сокращение полных фраз: «информация, представленная посредством непрерывных сигналов» и «информация, представленная посредством дискретных сигналов» — именно в таком контексте эти понятия будут использоваться в дальнейшем изложении. Поэтому когда заходит речь о видах информации, правильнее говорить о формах ее представления в сообщении или о видах сообщений.

Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого.

Знак — это элемент некоторого конечного множества отличных друг от друга сущностей.

Природа знака может любой — жест, рисунок, буква, сигнал светофора, определенный звук и т.д. Природа знака определяется носителем сообщения и формой представления информации в сообщении.

Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков.

Таким образом, набор есть дискретное множество знаков.

Набор знаков, в котором установлен порядок их следования, называется алфавитом.

Следовательно, алфавит — это упорядоченная совокупность знаков. Порядок следования знаков в алфавите называется лексикографическим. Благодаря этому порядку между знаками устанавливаются отношения «больше-меньше»: для двух знаков ξ и ψ принимается, что ξ

Примером алфавита может служить совокупность арабских цифр 0,1. 9 — с его помощью можно записать любое целое число в системах счисления от двоичной до десятичной. Если к этому алфавиту добавить знаки «+» и «-», то сформируется набор знаков, применимый для записи любого целого числа, как положительного, так и отрицательного; правда, этот набор нельзя считать алфавитом, поскольку в нем не определен порядок следования знаков. Наконец, если добавить знак разделителя разрядов («.» или «,»), то такой алфавит позволит записать любое вещественное число.

Поскольку при передаче сообщения параметр сигнала должен меняться, очевидно, что минимальное количество различных его значений равно двум и, следовательно, алфавит содержит минимум два знака — такой алфавит называется двоичным. Верхней границы числа знаков в алфавите не существует, примером могут служить иероглифы, каждый из которых обозначает целое понятие, и общее их количество исчисляется десятками тысяч.

Знаки, используемые для обозначения фонем человеческого языка, называются буквами, а их совокупность — алфавитом языка.

Сами по себе знак или буква не несут никакого смыслового содержания. Однако такое содержание им может быть приписано — в этом случае знак будет называться символом. (Например, массу в физике принято обозначать буквой m — следовательно, m является символом физической величины «масса» в формулах. Другим примером символов могут служить пиктограммы, обозначающие в компьютерных программах объекты или действия).

Таким образом, понятия «знак», «буква» и «символ» нельзя считать тождественными, (хотя весьма часто различия между ними не проводят, поэтому в информатике существуют понятия «символьная переменная», «кодировка символов алфавита», «символьная информация» — во всех приведенных примерах вместо термина «символьный» корректнее было бы использовать «знаковый» или «буквенный».)

Понятия знака и алфавита можно отнести только к дискретным сообщениям.

Так как имеются два типа сообщений, между ними, возможны четыре варианта преобразований (см. рис. 1.3):

Рис. 1.3. Варианты преобразований

Осуществимы и применяются на практике все четыре вида преобразований. Примерами устройств, в которых осуществляется преобразование типа N₁ → N₂ являются микрофон (звук преобразуется в электрические сигналы); магнитофон и видеомагнитофон (чередование областей намагничения ленты превращается в электрические сигналы, которые затем преобразуются в звук и изображение); телекамера (изображение и звук превращаются в электрические сигналы); радио- и телевизионный приемник (радиоволны преобразуются в электрические сигналы, а затем в звук и изображение); аналоговая вычислительная машина (одни электрические сигналы преобразуются в другие). Особенностью данного варианта преобразования является то, что оно всегда сопровождается частичной потерей информации. Потери связаны с помехами (шумами), которые порождает само информационное техническое устройство и которые воздействуют извне. Эти помехи примешиваются к основному сигналу и искажают его. Поскольку параметр сигнала может иметь любые значения (из некоторого интервала), то невозможно отделить ситуации: был ли сигнал искажен или он изначально имел такую величину. (В ряде устройств искажение происходит в силу особенностей преобразования в них сообщения, например в черно-белом телевидении теряется цвет изображения; телефон пропускает звук в более узком частотном интервале, чем интервал человеческого голоса; кино- и видеоизображение оказываются плоскими, они утратили объемность.)

Рассмотрим общий подход к преобразованию типа N → D. С математической точки зрения перевод сигнала из аналоговой формы в дискретную означает замену описывающей его непрерывной функции времени Z(t) на некотором отрезке [t₁, t₂] конечным множеством (массивом) i, t_i> (i = 0. n, где n — количество точек разбиения временного интервала). Подобное преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.

Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом Δt:

Квантование по величине — это отображение вещественных значений параметра сигнала в конечное множество чисел, кратных некоторой постоянной величине — шагу квантования (ΔZ).

Совместное выполнение обеих операций эквивалентно нанесению масштабной сетки на график Z(t), как показано на рис.1.4. Далее, в качестве пар значений i,_,t_i> выбираются узлы сетки, расположенные наиболее близко к Z(t_i). Полученное таким образом множество узлов оказывается дискретным представлением исходной непрерывной функции. Таким образом, любое сообщение, связанное с ходом Z(t), может быть преобразовано в дискретное, т.е. представлено посредством некоторого алфавита

Рис. 1.4. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине

При такой замене довольно очевидно, что чем меньше n (больше Δt, тем меньше число узлов, но и точность замены Z(t) значениями Z_i, будет меньшей. Другими словами, при дискретизации может происходить потеря части информации, связанной с особенностями функции Z(t). На первый взгляд кажется, что увеличением количества точек n можно улучшить соответствие между получаемым массивом и исходной функцией, однако полностью избежать потерь информации все равно не удастся, поскольку n — величина конечная.

Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:

Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.

Комментарии к теореме:

Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы.

Любое подобное устройство использует не весь спектр частот колебаний, а лишь какую-то его часть; например, в телефонных линиях используются колебания с частотами от 300 Гц до 3400 Гц. Согласно теореме отсчетов определяющим является значение верхней границы частоты — обозначим его V_m.

Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:

Можно перефразировать теорему отсчетов:

Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать Δt, определяемый в соответствии с (1.2).

Например, для точной передачи речевого сигнала с частотой до V_m = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале V_m ≈ 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.

Однако, помимо временной развертки, дискретизация имеет и другую составляющую — квантование. Выясним, как определяется шаг квантования ΔZ?

Любой получатель сообщения — человек или устройство — всегда имеют конечную предельную точность распознавания величины сигнала. (Например, человеческий глаз в состоянии различить около 16 миллионов цветовых оттенков; это означает, что при квантовании цвета нет смысла делать большее число градаций. При передаче речи достаточной оказывается гораздо меньшая точность — около 1%; следовательно, для амплитуды звуковых колебаний ΔZ ≈ 0,01*ΔZ max , а алфавит для обозначения всех градаций громкости должен содержать 100 знаков.)Таким образом, шаг квантования определяется чувствительностью приемного устройства.

Выбор шага развертки по времени и квантования по величине сигнала лежат в основе оцифровки звука и изображения. Примерами устройств, в которых происходят такие преобразования, являются сканер, модем, устройства для цифровой записи звука и изображения, лазерный проигрыватель, графопостроитель. Термины «цифровая запись», «цифровой сигнал» следует понимать как дискретное представление с применением двоичного цифрового алфавита.

Таким образом, преобразование сигналов типа N → D, как и обратное D → N, может осуществляться без потери, содержащейся в них информации.

Преобразование типа D₁ → D₂ состоит в переходе при представлении сигналов от одного алфавита к другому — такая операция носит название перекодировка и может осуществляться без потерь. Примерами ситуаций, в которых осуществляются подобные преобразования, могут быть: запись-считывание с компьютерных носителей информации; шифровка и дешифровка текста; вычисления на калькуляторе.

Таким образом, за исключением N₁ → N₂ в остальных случаях оказывается возможным преобразование сообщений без потерь содержащейся в них информации. При этом на первый взгляд непрерывные и дискретные сообщения оказываются равноправными. Однако на самом деле это не так. Сохранение информации в преобразованиях N → D и D → N обеспечивается именно благодаря участию в них дискретного представления. Другими словами, преобразование сообщений без потерь информации возможно только в том случае, если хотя бы одно из них является дискретным. В этом проявляется несимметричность видов сообщений и преимущество дискретной формы. К другим ее достоинствам следует отнести:

• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;

• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;

Последнее качество — универсальность — оказывается следствием того обстоятельства, что любые дискретные сообщения, составленные в различных алфавитах, посредством обратимого кодирования можно привести к единому алфавиту. Это позволяет выделить некоторый алфавит в качестве базового (из соображений удобства, простоты, компактности или каких-либо иных) и представлять в нем любую дискретную информацию. Тогда устройство, работающее с информацией в базовом алфавите, оказывается универсальным в том отношении, что оно может быть использовано для переработки любой иной исходной дискретной информации. Таким базовым алфавитом, как увидим в дальнейшем, является двоичный алфавит, а использующим его универсальным устройством — компьютер.

Информация, порождаемая и существующая в природе, связана с материальным миром — это размеры, форма, цвет и другие физические, химические и прочие характеристики и свойства объектов. Данная информация передается посредством физических и иных взаимодействий и процессов. Эту природную информацию можно считать хаотической и неупорядоченной, поскольку никем и ничем не регулируется ее появление, существование, использование. Чаще всего она непрерывна по форме представления. Напротив, дискретная информация — это информация, прошедшая обработку — отбор, упорядочение, преобразование; она предназначена для дальнейшего применения человеком или техническим устройством. Другими словами, дискретная — это уже частично осмысленная информация, т.е. имеющая для кого-то смысл и значение и, как следствие, более высокий (с точки зрения пользы) статус, нежели непрерывная.

Источник