Преобразование суждений
Для выяснения точного логического смысла суждения нередко требуется преобразование его формы. Это достигается прежде всего посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату.
Обращение — это преобразование суждения путем перестановки его субъекта и предиката местами. При этом количество суждения (кванторное слово) может изменяться, а качество не меняется.
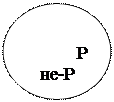
а) Общеутвердительное суждение (А) преобразуется в частноутвердительное (I). Обусловлено это тем, что субъект в нем распределен, а предикат, как правило, не распределен, формула обращения «Все S есть Р» — «Некоторые Р есть S». Так, в суждении «Все змеи — ядовитые существа» поставим субъект на место предиката, а предикат на место субъекта. В результате получим «Некоторые ядовитые существа — змеи». Это графически можно представить так:
где S — змеи, Р — ядовитые существа. Такое преобразование называется «обращение с ограничением».
б) Частноутвердительное суждение (I) обращается в частноутвердительное (I). Субъект и предикат в них, как правило, не распределены. Формула об-
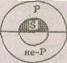
ращения «Некоторые S есть Р» — «Некоторые Р есть S». Пример: «Некоторые поэты — талантливые люди» — «Некоторые талантливые люди — поэты». На круговой схеме:
Исключение составляют суждения, в которых субъект не распределен, а предикат распределен.
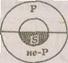
в) Общеотрицательное суждение (Е) обращается в общеотрицательное (Е), так как субъект и предикат здесь распределены. Формула: «Ни одно S не есть Р» — «Ни одно Р не есть S». Например: «Ни один друг не может быть предателем» — «Ни один предатель не может быть другом».
 |  |
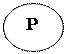г) Частноотрицательные суждения не обращаются. Субъект в них не распределен, следовательно, он не может стать предикатом нового, тоже отрицательного суждения, где предикат всегда распределен. Попробуем для примера выяснить, что произойдет с суждением «Некоторые мужчины — неженатые». Означает ли оно, что «Ни один женатый — не мужчина»? Или только «некоторые»? И тот и другой вывод бессмысленны. А иного сделать нельзя. Это видно на схеме:
 |
Превращение — это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются. В превращении проявляются следующие закономерности: а) общеутвердительное суждение (А) преобразуется в общеотрицательное (Е). Формула превращения: «Все S есть Р» — «Ни одно S не есть не-Р». Так, суждение «Все волки — хищники» по качеству утвердительное. Превращаем его в отрицательное, но так при этом, чтобы его смысл не изменился: «Ни один волк не является нехищником». Вот графическое изображение:
 |
б) Общеотрицательное суждение (Е), наоборот, превращается в общеутвердительное (А). Формула: «Ни одно S не есть не-Р» — «Все S есть Р». Пример: «Ни одно преступление не осталось безнаказанным» — «Все преступления наказаны». Графически:
 |
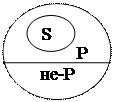в) Частноутвердительное суждение (I) превращается в частноотрицательное (О), формула «Некоторые S есть Р» — «Некоторые S не есть не-Р». Пример:
«Некоторые свидетели дали верные показания» — «Некоторые свидетели не дали неверных показаний». Графически:
г) Частноотрицательное суждение (О) превращается в частноутвердительное (I). Формула: «Некоторые S не есть Р» — «Некоторые S есть не-Р». Например: «Некоторые книги не есть интересные» — «Некоторые книги есть неинтересные». Графически:
Значение превращения как логической операции состоит в том, что благодаря ему в суждении раскрывается новый, более богатый смысл: утверждение принимает форму отрицания и наоборот.
Обращение и превращение выступают исходными логическими операциями с суждениями. Их различное сочетание порождает еще две операции: противопоставление субъекту и противопоставление предикату, которые считаются производными или смешанными.
Противопоставление субъекту — так называется преобразование суждения путем обращения и последующего превращения. Приведем для краткости лишь один пример. Если суждение «Все волки — хищники» сначала обратим в суждение «Некоторые хищники — волки», а это последнее, в свою очередь, превратим в суждение «Некоторые хищники не есть неволки», то получим противопоставление субъекту. Предикат заключительного суждения — «неволки» — противопоставляется субъекту исходного суждения — «волки». Отсюда название самой операции.
Противопоставление предикату — это преобразование суждения путем превращения и последующего обращения. Пример: суждение «Все волки — хищники» сначала превратим в суждение «Ни один волк не является нехищником», а это последнее обратим в суждение «Ни один нехищник не является волком». Получается, что предикату исходного суждения «хищники» мы противопоставили понятие «нехищники» и сделали его субъектом нового суждения. Этим объясняется название операции.
Другую важнейшую логическую операцию представляет собой отрицание суждений, или инверсия (от лат. inversio — «переворачивание»). Его сходство с преобразованием суждений состоит в том, что результатом отрицания выступает тоже новое суждение. Отличие состоит в процессе преобразования суждения: как мы видели, меняется лишь его логическая форма, тогда как смысл остается тем же самым. В процессе же отрицания меняется не только форма суждения, но и самый его смысл: оно становится противоречащим исходному, исключающим его. Таким образом, если в основе преобразования суждений лежит их эквивалентность по смыслу, то в основе отрицания — их несовместимость.
Рассмотрим вначале отрицание простых атрибутивных суждений, которое заключается в замене одного исходного суждения другим, не только несовместимым с ним, но и противоречащим ему. Языковыми средствами выражения такой операции служат обороты речи типа «неверно, что. » или частица «не» и ей подобные.
Если формула простого атрибутивного утвердительного суждения — «S есть Р», то формулой отрицания его будет: «Неверно, что S есть Р» или «S не есть Р». В символической записи: Ā (читается: «неверно, что А»; «не-А»). Например: «Все мужья верны своим женам» — «Неверно, что все мужья верны своим женам » или «Не все мужья верны своим женам «. Отрицанию могут подвергаться и отрицательные суждения. Если формула отрицательного суждения — «S не есть Р», то его отрицание будет выражено формулой: «Неверно, что S не есть Р» (что равносильно утверждению: «S есть Р»).
1. Какова логическая структура суждения?
2. Назовите основные виды предложений.
3. Что такое классификация?
4. Какие виды простых суждений Вы знаете?
5. В каком случае термин считается распределенным?
6. Охарактеризуйте атрибутивные реляционные и экзистенциальные суждения.
7. Что такое модальные высказывания? Перечислите их основные виды.
8. Назовите виды сложных суждений.
9. Каковы отношения между простыми суждениями (по логическому квадрату)?
10.Характеризуйте основные типы преобразования суждений: обращение, превращение, противопоставление субъекту, противопоставление предикату, инверсия.
Источник
Преобразование простых суждений
Логическая операция преобразования простого суждения предполагает изменение его формы, или структуры, но не со- держания. В результате преобразования простого суждения его содержание должно оставаться неизменным. Распределенность терминов в исходном суждении и в новом суждении должна оставаться одной и той же (термин, который был распределен в исходном суждении, должен быть распределен и в новом суждении, то же самое и с нераспределенным термином). Существует три способа преобразования простых суждений: обращение, превращение и противопоставление предикату.
Обращение (также часто называемое конверсией) – это преобразование простого суждения, при котором его субъект и предикат меняются местами. Например, суждение: Все акулы являются рыбами преобразуется путем обращения в суждение: Некоторые рыбы являются акулами.
Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора все, а новое – с квантора некоторые? Этот вопрос, на первый взгляд, кажется странным, ведь нельзя же сказать: Все рыбы являются акулами, следовательно, единственное, что остается, это: Некоторые рыбы являются акулами. Однако, в данном случае, мы обратились к содержанию суждения и по смыслу поменяли квантор все на квантор некоторые; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой, будучи формальной логикой.
Поэтому обращение суждения: Все акулы являются рыбами можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределенность терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект (акулы) и предикат (рыбы) находятся в данном случае в отношении подчинения:
На схеме видно, что субъект распределен (полный круг), а предикат нераспределен (неполный круг). Вспомнив, что тер- мин распределен, когда речь идет обо всех предметах, входящих в него и нераспределен, когда – не обо всех (см. предыдущий параграф), мы автоматически мысленно ставим перед термином акулы квантор все, а перед термином рыбы квантор некоторые.
Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина рыбы, мы опять же автоматически снабжаем его квантором некоторые, не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: Некоторые рыбы являются акулами. Возможно, все это покажется чрезмерным усложнением элементарной операции, однако, как увидим далее, в иных случаях преобразование суждений сделать непросто без использования распределенности терминов и круговых схем.
Обратим внимание на то, что в рассмотренном выше при- мере исходное суждение было вида А, а новое – вида I, т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях: Все акулы являются рыба- ми и Некоторые рыбы являются акулами речь идет об одном и том же.
Рассмотрим все случаи обращения в зависимости от вида простого суждения и характера отношений между его субъектом и предикатом.
1. Суждение вида А, в котором субъект и предикат находятся в отношении равнозначности, обращается в суждение вида А : Все квадраты (S) – это равносторонние прямоугольники (P) ? Все равносторонние прямоугольники – это квадраты.
2. Суждение вида А, в котором субъект и предикат находятся в отношении подчинения, обращается в суждение вида I: Все сосны (S) являются деревьями (S) Некоторые деревья являются соснами.
3. Суждение вида I, в котором субъект и предикат находятся в отношении пересечения, обращается в суждение вида I: Некоторые школьники (S) – это спортсмены (P) Некоторые спортсмены – это школьники.
4. Суждение вида I, в котором субъект и предикат находят- ся в отношении подчинения, обращается в суждение вида А: Некоторые книги (S) являются учебниками (P) Все учебники являются книгами.
5. Суждение вида Е, в котором субъект и предикат находятся только в отношении несовместимости, всегда обращается в суждение вида Е: Все планеты (S) не являются звездами (Р) ? Все звезды не являются планетами.
6. Если попытаться подвергнуть обращению суждение вида О, то вместе с изменением его формы изменится и его содержание, которое, как мы помним, меняться не должно; т. е. суждения вида О не поддаются обращению: Некоторые школьники (S) не являются спортсменами (Р) ? Все спортсмены не являются школьниками. В данном случае новое суждение имеет квантор «все», потому что предикат исходного суждения представляет собой распределенный термин:
Приведем еще один пример, иллюстрирующий невозможность преобразования суждений вида О путем обращения: Не- которые книги (S) не являются учебниками (Р) ? Все учебники не являются книгами.
Итак, суждение вида А обращается или в суждение вида А, или в суждение вида I. Суждение вида I обращается или в суждение вида I, или в суждение вида А. Суждение вида Е всегда обращается в суждение вида Е, а суждение вида О не поддается обращению.
Второй способ преобразования простых суждений, называемый превращением (или обверсией), заключается в том, что у суждения меняется связка: положительная на отрицательную или наоборот. При этом предикат суждения заменяется противоречащим понятием.
Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения: Все акулы являются рыбами преобразуется путем превращения в суждение Все акулы не являются не рыбами. Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект (акулы) и предикат (не рыбы) суждения, получившегося в результате превращения, находятся в отношении несовместимости:
Приведенный пример превращения демонстрирует важную логическую закономерность, которая заключается в том, что любое утверждение равно двойному отрицанию (и наоборот). Как видим, исходное суждение вида А в результате превращения стало суждением вида Е. В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида А всегда превращается в суждение вида Е, а суждение вида Е всегда превращается в суждение вида А. Суждение вида I всегда превращается в суждение вида О, а суждение вида О всегда превращается в суждение вида I.
Третий способ преобразования простых суждений – противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы преобразовать путем противопоставления предикату суждение: Все акулы являются рыбами надо сначала подвергнуть его превращению. Получится: Все акулы не являются не рыбами. Теперь надо совершить обращение с этим получившимся суждением, т. е. поменять местами его субъект (акулы) и предикат (не рыбы). В данном случае, чтобы не ошибиться, вновь прибегнем к установлению распределенности терминов с помощью круговой схемы. Субъект и предикат в этом суждении находятся в отношении несовместимости:
На схеме видим, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно мы должны сопроводить как субъект, так и предикат квантором все. После этого совершим обращение с суждением: Все акулы не являются не рыбами. Получится: Все не рыбы не являются акулами. Суждение звучит непривычно, потому что оно представляет собой более короткую формулировку той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе.
Обращение можно было сделать и проще: вспомнив, что суждение вида Е всегда обращается в суждение вида Е, мы могли, не используя круговой схемы и не устанавливая распределенности терминов, сразу поставить перед предикатом (не рыбы) квантор все. Однако, в данном случае был предложен другой способ, чтобы показать, что вполне можно обойтись без запоминания рассмотренных выше алгоритмов для обращения. (Здесь происходит примерно то же самое, что в математике: можно запоминать различные формулы, но также возможно обойтись и без запоминания, т. к. любую формулу нетрудно вывести самостоятельно).
Проще всего совершать все три операции преобразования простых суждений с помощью круговых схем. Для этого надо изобразить кругами Эйлера три термина: субъект, предикат и понятие, противоречащее предикату (не – предикат). Потом следует установить их распределенность, и из получившейся схемы будут вытекать четыре суждения: одно исходное и три результата преобразований.
Главное, помнить, что распределенный термин соответствует квантору все, а нераспределенный – квантору некоторые, и также, что соприкасающиеся на схеме круги соответствуют связке является, а несоприкасающиеся – связке не является. Например, требуется совершить три операции преобразования с суждением: Все учебники являются книгами. Изобразим субъект (учебники), предикат (книги) и не – предикат (не книги) кругами Эйлера и установим распределенность этих терминов:
Получившуюся схему можно прочитать четырьмя способами:
- Все учебники являются книгами (исходное суждение).
- Некоторые книги являются учебниками (обращение).
- Все учебники не являются не книгами (превращение).
- Все не книги не являются учебниками (противопоставление предикату).
Рассмотрим еще один пример. Надо преобразовать тремя способами суждение: Все планеты не являются звездами. Изобразим кругами Эйлера субъект (планеты), предикат (звезды) и не – предикат (не звезды). Обратите внимание на то, что понятия планеты и не звезды находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределенность этих терминов:
Получившуюся схему можно прочитать четырьмя разными способами:
- Все планеты не являются звездами (исходное суждение).
- Все звезды не являются планетами (обращение).
- Все планеты являются не звездами (превращение).
- Некоторые не звезды являются планетами (противопоставление предикату).
В заключение еще раз отметим, что частноотрицательные суждения (О) не поддаются обращению. Из этого следует, что частноутвердительные суждения (I) не поддаются операции противопоставления предикату, которая состоит из последовательно проведенных превращения и обращения. Частно- утвердительное суждение (I) в результате превращения становится частноотрицательным суждением (О), которое следует подвергнуть обращению, что сделать невозможно по причине необращаемости суждений вида О.
Источник
