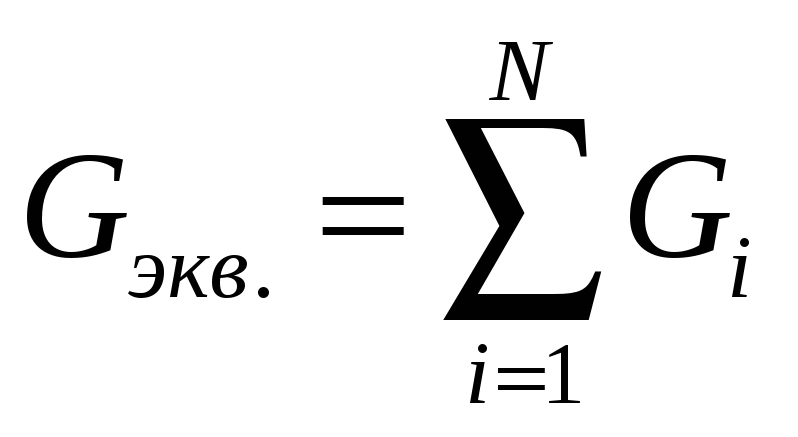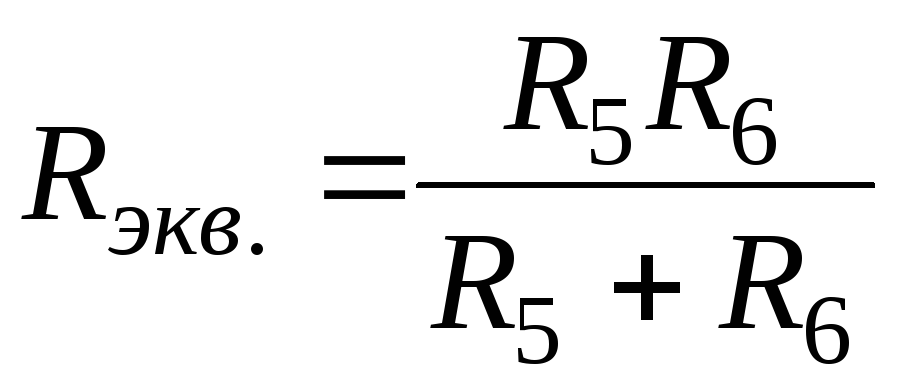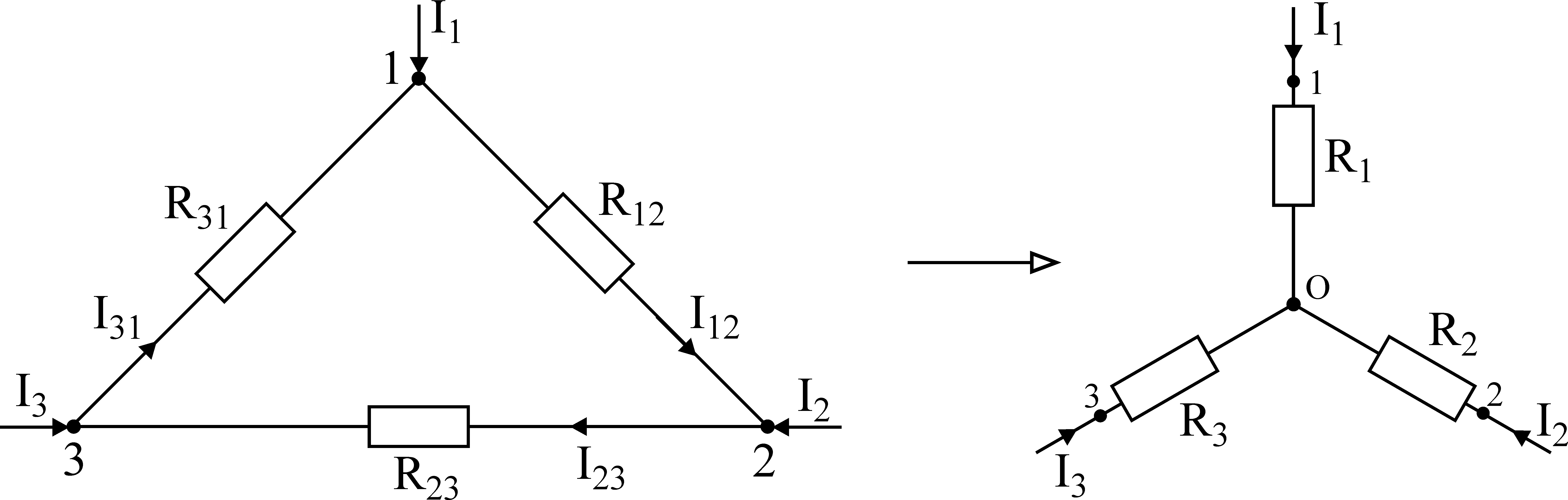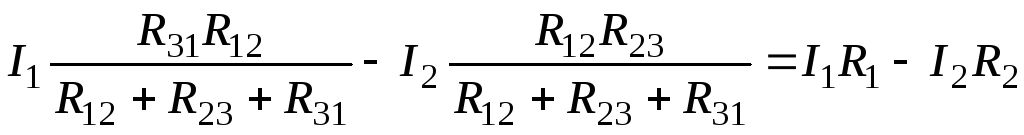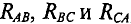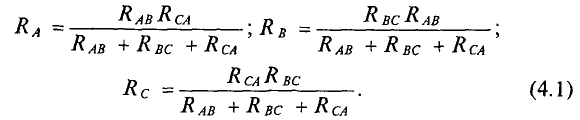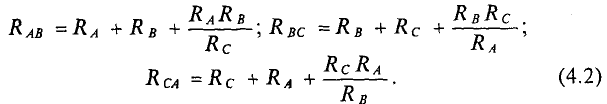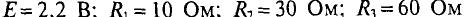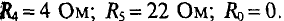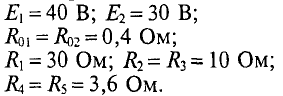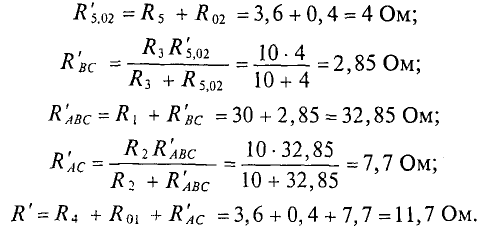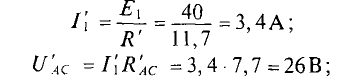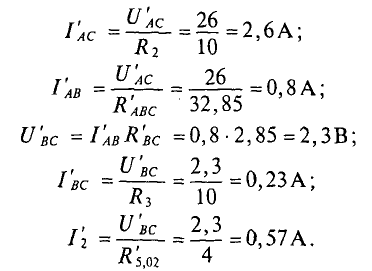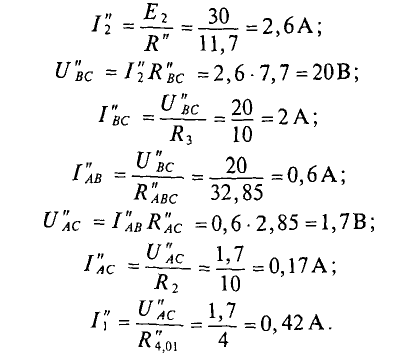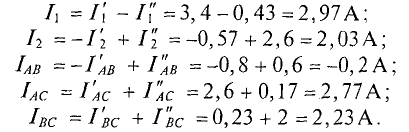Способы преобразования электрических цепей

Лекция III.

Ознакомившись с данной лекцией, студенты должны знать:

Цель преобразования электрических цепей.

Четко различать участки с последовательным и параллельным соединениями при рассмотрении смешанного соединения проводов.

Уметь преобразовывать соединение треугольник в эквивалентную звезду и обратно.

Уметь преобразовать источник напряжения в источник тока и обратно.

Преобразование схем электрических цепей.

Целью преобразования электрических цепей является их упрощение, это необходимо для простоты и удобства расчета.

Одним из основных видов преобразования электрических схем является преобразование схем со смешанным соединением элементов. Смешанное соединение элементов – это совокупность последовательных и параллельных соединений, которые и будут рассмотрены в начале данной лекции.

На рис. 3-1 изображена ветвь электрической цепи, в которой последовательно включены сопротивления R₁, R₂,…,R_n. Через все эти сопротивления проходит один и тот же ток I. Напряжения на отдельных участках цепи обозначим через U₁, U₂,…, U_n.

Рис. 3-1 Последовательное соединение.

По ЗНК напряжение на ветви

Сумма сопротивлений всех участков данной ветви

Называется эквивалентным последовательным сопротивлением.

Поскольку напряжения, которые падают на отдельных сопротивлениях, пропорциональны этим сопротивлениям, можно сказать, что последовательно включенные сопротивления образуют «делитель напряжения». Понятие делителя напряжения широко используется в технике.

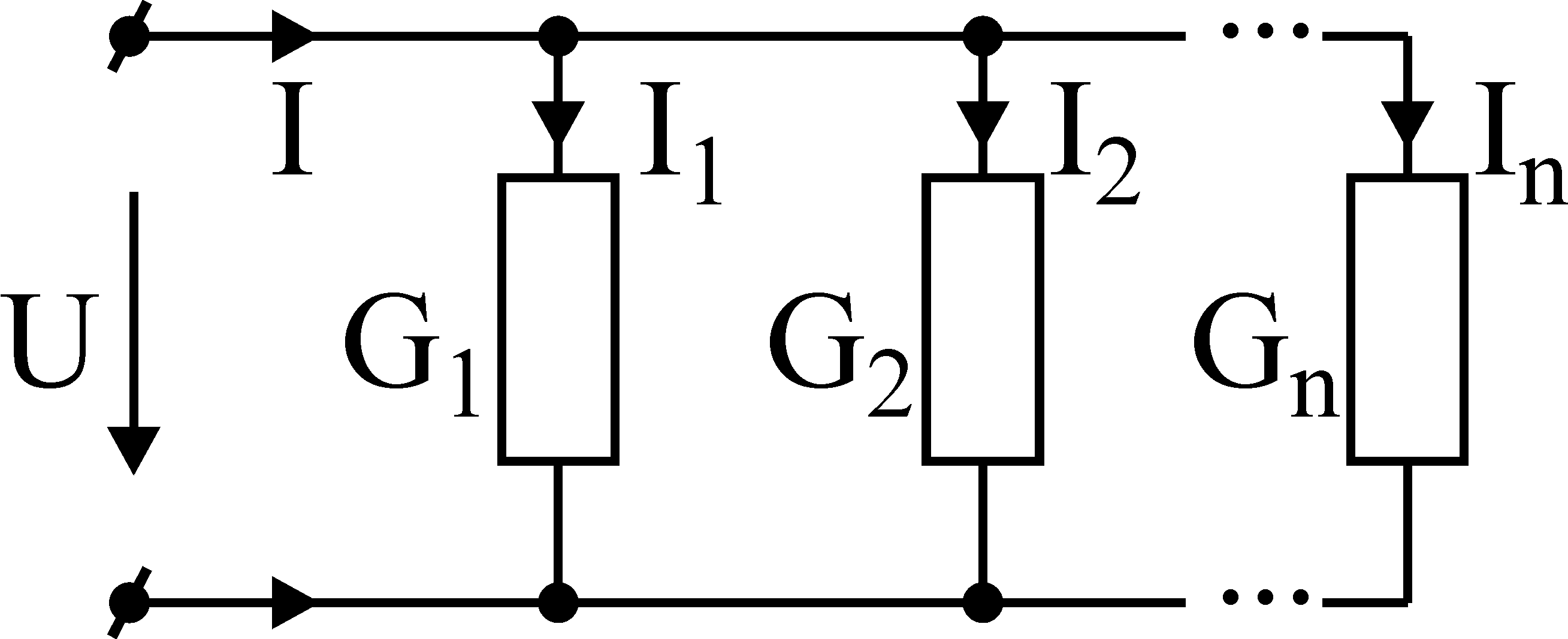
На рис. 3-2 изображена схема электрической цепи с двумя узлами, между которыми включено n параллельных ветвей с проводимостями G₁, G₂,…, G_n. Напряжение между узлами U, оно одинаково для всех ветвей.

Рис.3-2 Параллельное соединение (показать преобразованное).

По ЗТК общий то равен сумме токов отдельных ветвей:

Сумма проводимостей всех ветвей, соединенных параллельно

называется эквивалентной проводимостью.

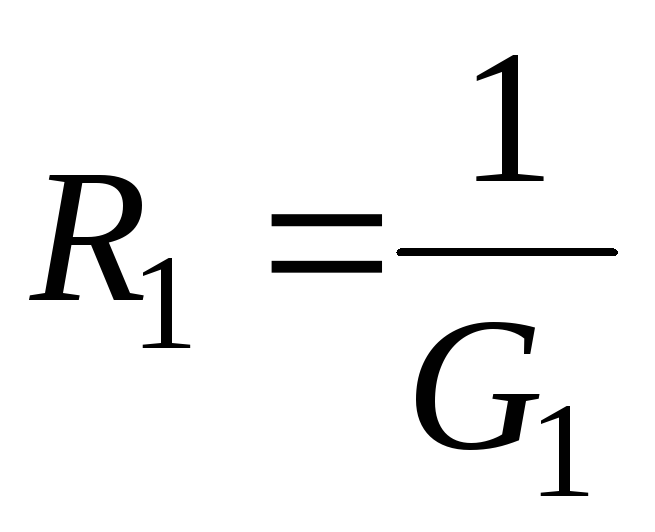
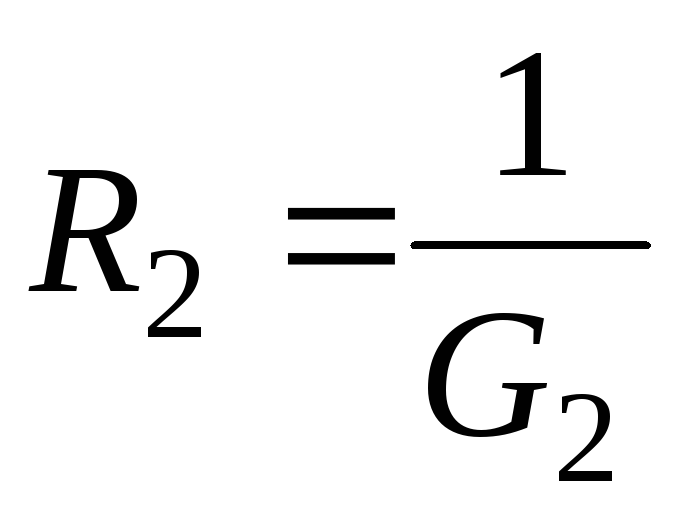
В случае параллельного сопротивления двух ветвей (n=2) обычно пользуются выражениями, в которые входят сопротивления и .

Эквивалентное сопротивление двух параллельно соединенных ветвей равно:

. (3)

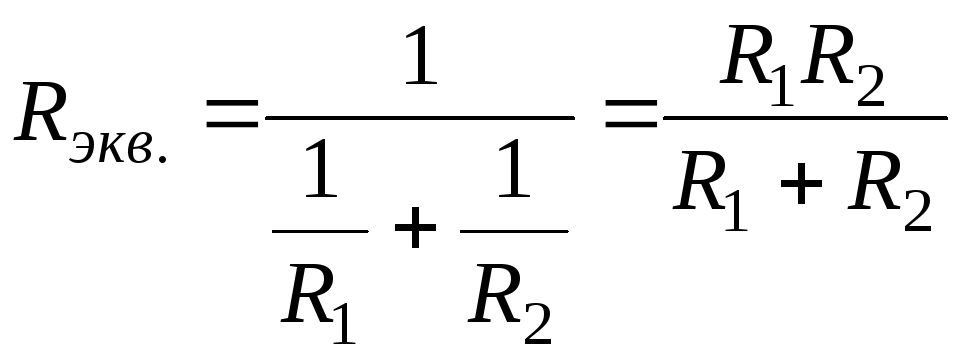
Поскольку общий ток делится на отдельные токи ветвей пропорционально проводимостям этих ветвей (или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей), можно сказать, что параллельно включенные сопротивления образуют «делитель токов». Понятие делителя токов используется в технике.

Часто при использовании «ручного» расчета электрических цепей необходимо определить, как ток разделяется по отдельным ветвям параллельно соединенных ветвей.

Из формулы (2) следует, что токи ветвей, соединенных параллельно, пропорциональны проводимостям этих ветвей, т.е. токи делятся по ветвям пропорционально сопротивлениям этих ветвей, или, что тоже самое, обратно пропорционально сопротивлениям этих ветвей.

В случае двух параллельно соединенных сопротивления их общее сопротивление (2) равно:

, тогда суммарный ток I, протекающий по этому эквивалентному сопротивлению, создаст напряжение U, равное:

, чтобы найти ток I₁ в сопротивлении R₁, необходимо разделить выражение на R₁ , а чтобы найти ток I₂ в сопротивлении R₂ найти разделить выражение на R₂:

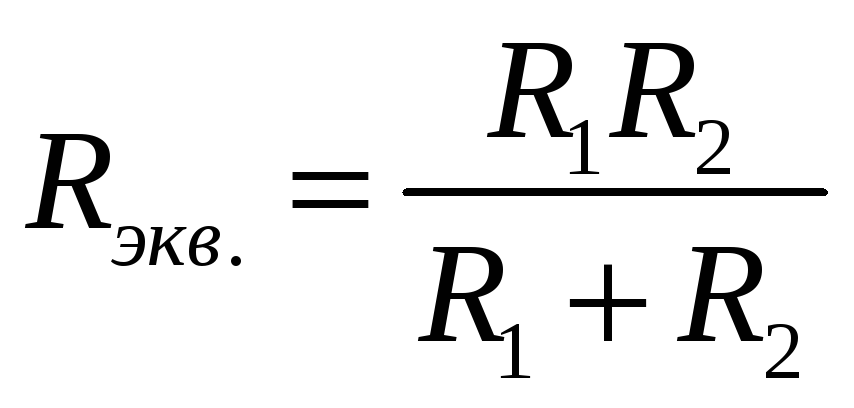
Полученные выражения для токов иногда называют «правилом плеч», которое гласит: ток делится между параллельно включенными сопротивлениями (в делителе токов) обратно пропорционально этим сопротивлениям.

(4)

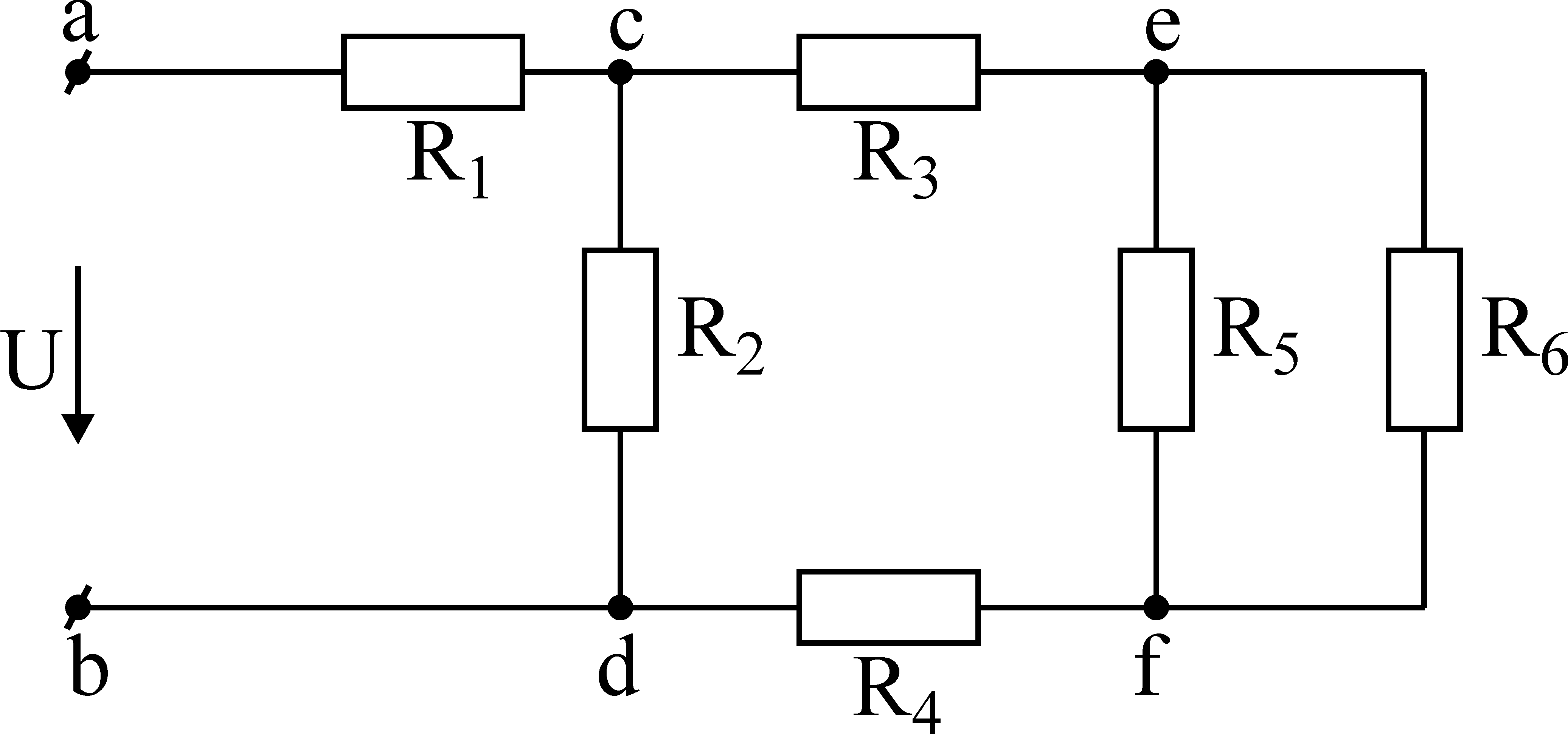
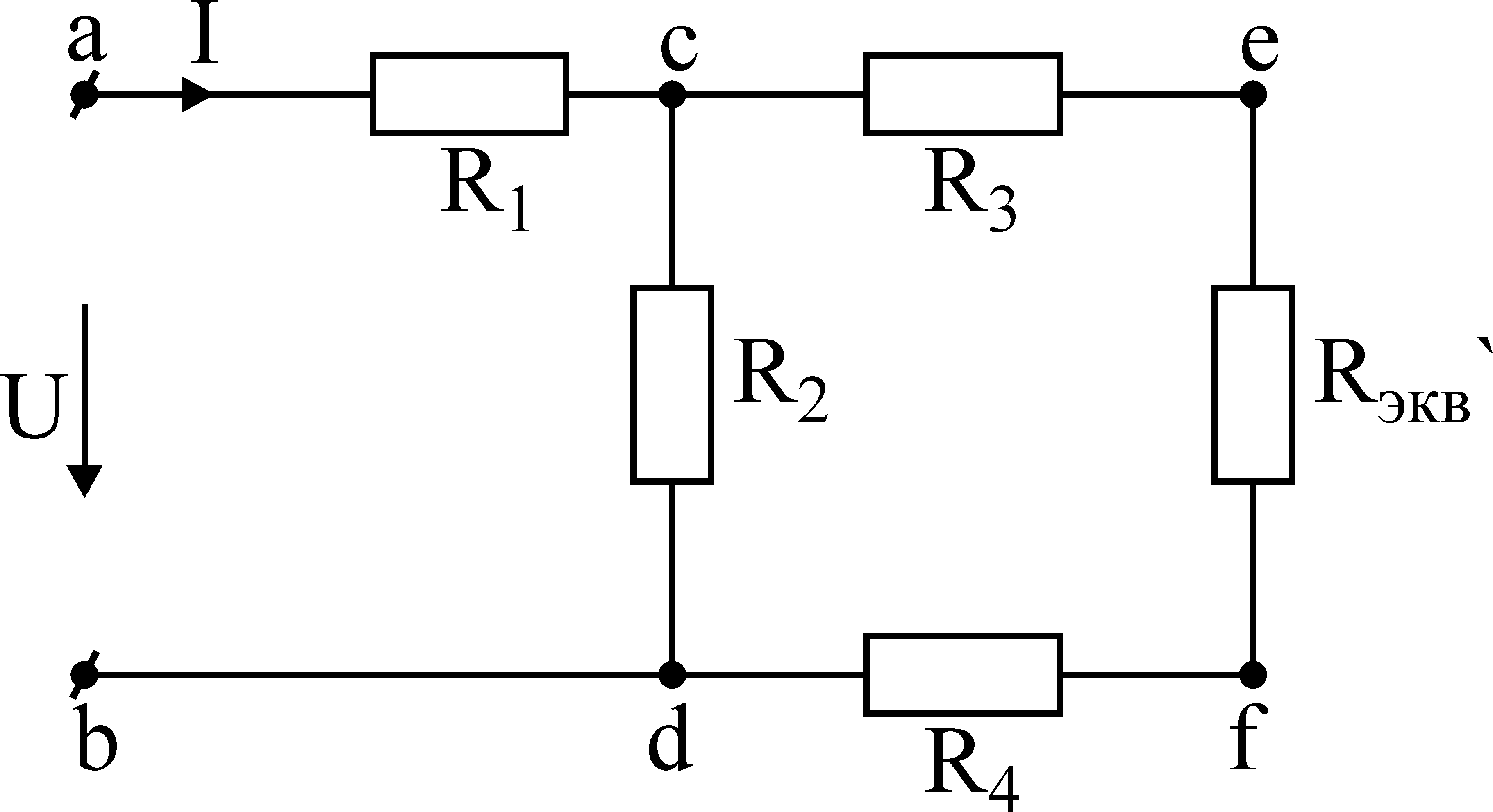
На рис.3-3 показано смешанное соединение электрической цепи:

Рис.3-3 Смешанное соединение.

Эта схема легко приводится к одноконтурной. Сопротивления R₅ и R₆ включены параллельно, поэтому необходимо вычислить эквивалентное сопротивление данного участка по формуле

Для понимания полученного результата можно изобразить промежуточную схему (рис. 3-4).

Сопротивления R₃, R₄ и R / _экв. соединены последовательно, и эквивалентное сопротивление участка c-e-f-d равно:

После этого этапа преобразований схема приобретает вид рис. 3-5.

Затем находим эквивалентное сопротивление участка c-d и суммируем его с сопротивлением R₁. Общее эквивалентное сопротивление равно:

.

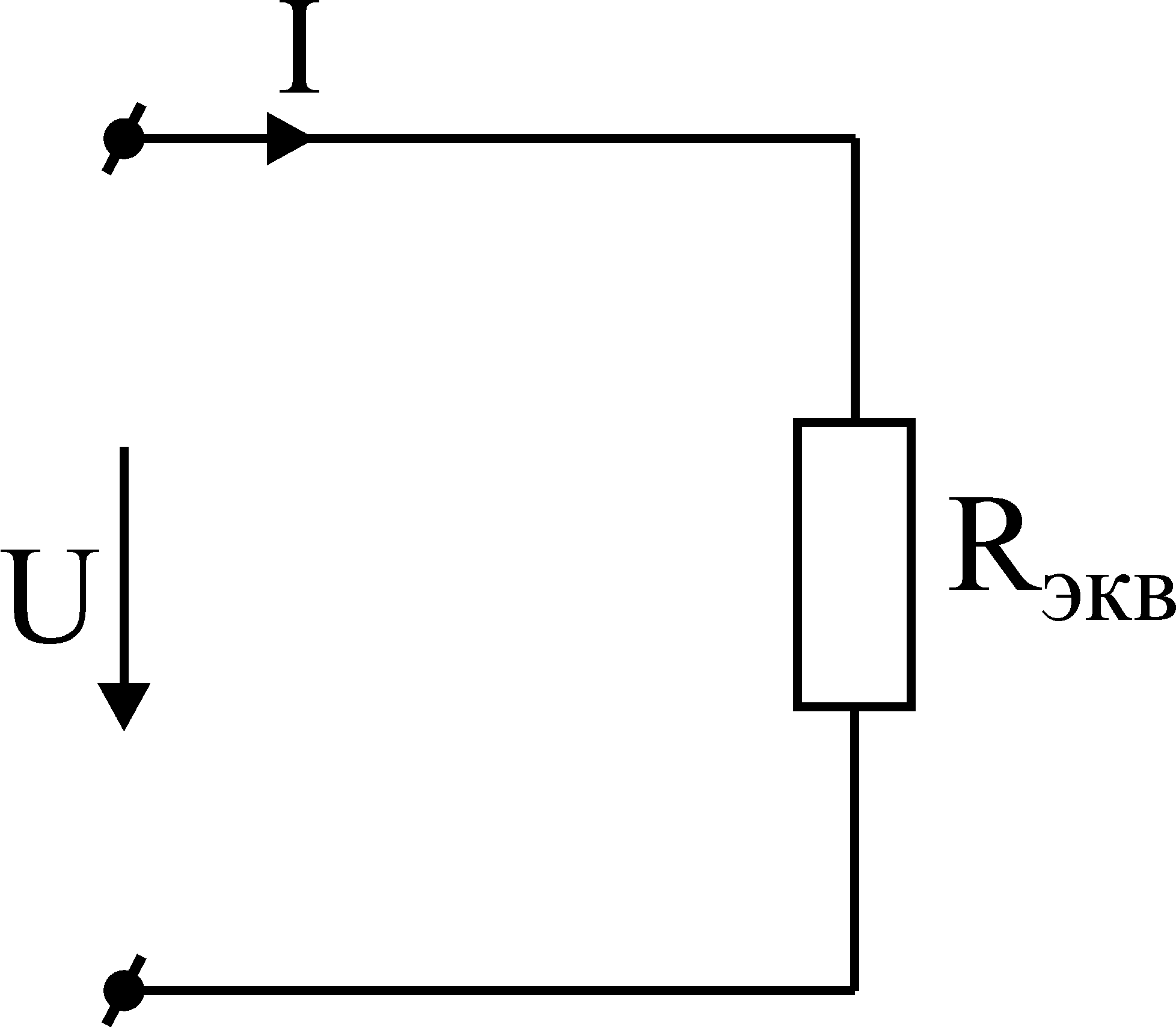
Полученное сопротивление эквивалентно сопротивлению (рис. 3-6) исходной схемы со смешанным соединением. Понятие “эквивалентно” означает, что напряжение U на входных зажимах и ток I входной ветви остаются неизменными на протяжении всех преобразований.

Преобразование треугольника в эквивалентную звезду.

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.

Т.е., под эквивалентностью треугольника и звезды понимается то, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные выводы, одинаковы.

Рис. 3-7. Преобразование треугольника в звезду.

Пусть R₁₂; R₂₃; R₃₁— сопротивления сторон треугольника;

I₁₂; I₂₃; I₃₁— токи в ветвях треугольника;

I₁; I₂; I₃— токи, подходящие к зажимам 1, 2, 3.

Выразим токи в ветвях треугольника через подходящие токи I₁, I₂, I₃.

По закону напряжений Кирхгофа сумма падений напряжений в контуре треугольника равна нулю:

По закону токов Кирхгофа для узлов 1 и 2

При решении этих уравнений относительно I₁₂ получим:

Напряжение между точками 1 и 2 схемы треугольника:

Напряжение между этими же точками схемы звезды равно:

Т.к. речь идет об эквивалентном преобразовании, то необходимо равенство напряжений между данными точками двух схем, т.е.

Это возможно при условии:

(5)

Третье выражение получено в результате круговой замены индексов.

Исходя из выражения (5) формулируется следующее правило:

Сопротивление луча звезды равно произведению сопротивлений сторон треугольника, прилегающих к этому лучу, деленному на сумму сопротивлений трех сторон треугольника.

Преобразование звезды в эквивалентный треугольник.

При переходе от звезды к треугольнику известными являются сопротивления R₁, R₂, R₃ лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений (5):

(6)

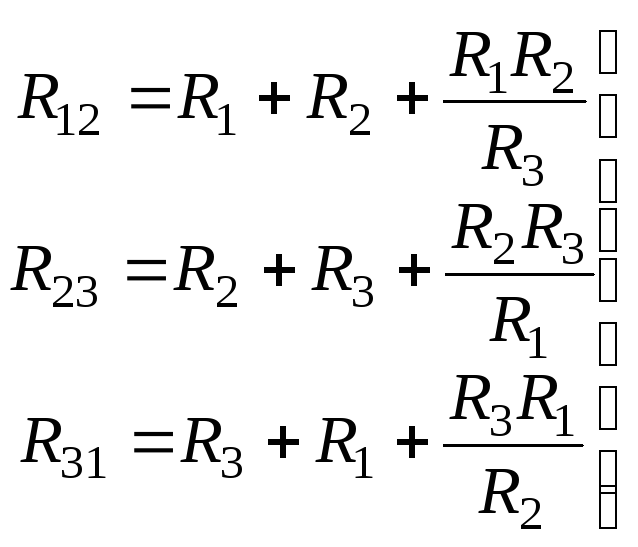
Сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Метод преобразования схем электрических цепей

Метод преобразования схем:

Метод преобразования электрических схем применяют для расчета сложных цепей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.

Контур, состоящий из трех сопротивлений

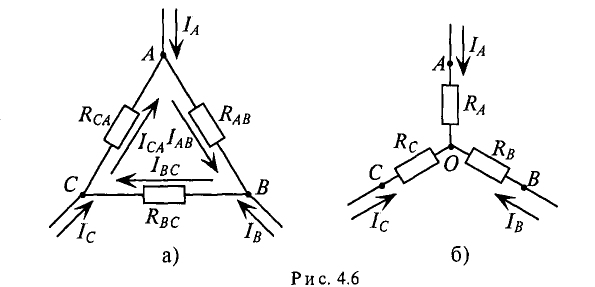
Электрическая цепь, состоящая из трех сопротивлений Ra, Rb и Rc, соединенных в одной узловой точке О, образует звезду сопротивлений (рис. 4.66).

Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треугольником или наоборот.

Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками А, В и С токи 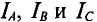звезды и треугольника оставались без изменений.

Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.

Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинами А, В, и С и к этим обозначенным вершинам подсоединить эквивалентную звезду (или треугольник).

При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.

При замене звезды эквивалентным треугольником каждое составление треугольника определяется следующими выражениями:

Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.

Пример 4.4

Определить токи во всех ветвях цепи (рис. 4.7а) при следующих сходных данных:

Решение

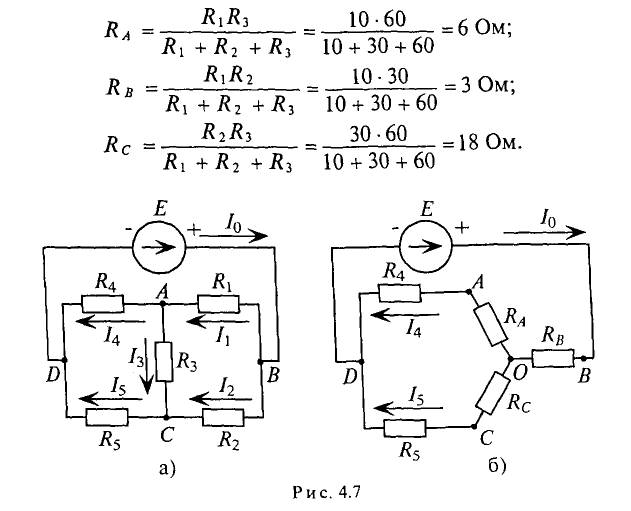
Для расчета этой цепи заменим треугольник сопротивлений, подключенных к точкам А, В и С, эквивалентной звездой, подученной к тем же точкам (рис. 4.76). Определим величины сопротивлений эквивалентной звезды:

Пример 4.6

Определить токи во всех ветвях цепи, схема которой приведена на рис. 4.8а, если задано:

Решение

Количество ветвей и соответственно различных токов в цепи (рис. 4.8а) равно пяти. Произвольно выбирается направление этих токов.

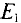
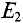
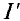
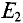
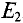
Расчетных схем две, так как в цепи два источника с ЭДС и . Вычисляются частичные токи, созданные в ветвях первым источником . Для этого изображается та же цепь, только вместо — его внутреннее сопротивление Направление частичных токов в ветвях указаны в схеме рис. 4.86.

Вычисление сопротивлений и токов производится методом свертывания.

Первые частичные токи в цепи (рис. 4.86), созданные источником Еи имеют следующие значения:

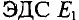
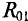
Вычисляются частичные токи, созданные вторым источником. Для этого изображается исходная цепь, в которой источник заменен его внутренним сопротивлением . Направления частичных токов в ветвях указаны на схеме рис. 4.8в. Сопротивления и токи определяются методом свертывания.

Вторые частичные токи в цепи (рис. 4.8в) имеют следующие значения:

Искомые токи в рассматриваемой цепи (рис. 4.8а) определяют алгебраической суммой частичных токов (см. рис. 4.8):

Ток 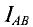имеет знак «минус», следовательно, его направлен противоположно произвольно выбранному, он направлен из точки А в точку В.

Рекомендую подробно изучить предметы:

Электротехника Основы теории цепей

Ещё лекции с примерами решения и объяснением:

• Параллельное соединение генераторов
• Метод узловых и контурных уравнений
• Метод эквивалентного генератора
• Теоремы теории цепей
• Входные и взаимные проводимости
• Преобразование треугольника сопротивлений в эквивалентную звезду
• Метод контурных токов
• Метод свертывания электрической цепи

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник